Лабораторна робота № 3. Методи нульового порядку функції багатьох змінних

Мета: дослідити використання методів нульового порядку для розв'язання задачі багатомiрної оптимізації

Теоретичні відомості

До методів нульового порядку відноситься пошук за симплексом (не плутати з симплекс методом в лінійному програмуванні), метод покоординатного спуску Гауса-Зейделя, випадковий пошук та інші.

Пошук за симплексом [4] полягає в тому, що під час пошуку оптимуму в просторі незалежних змінних будується регулярний симплекс і обчислюється значення цільової функції в його вершинах. Регулярний симплекс у n-мірному просторі представляє собою багатогранник, який має n+1 рівновіддалених вершин. Наприклад, у випадку двох змінних симплексом є рівнобічний трикутник; в трьохвимірному просторі симплекс представляє собою тетраедр. Після побудови симплекса визначається вершина, яка має найбільше значення цільової функції. На рис.2 це вершина під номером 1.

Знайдена вершина проектується через центр ваги інших вершин симплекса (точки 2 і 3) у нову вершину (точка 4). Точки 2-4 використовуються в якості вершин нового симплекса. Таким чином, трикутник немов би перевертається через сторону з найменшим значенням цільової функції. Під час пошуку мінімуму використовуються такі два правила:

Правило “накриття” точки мінімуму. Якщо вершина, якій відповідає найбільше значення цільової функції, побудована на попередній ітерації, то замість неї береться вершина з меншим значенням цільової функції.

Правило циклічного руху. Якщо деяка вершина симплекса не виключається протягом багатьох ітерацій, то необхідно зменшити розмір симплекса.

Пошук завершується, коли розмір симплекса чи різниця між значеннями функції у вершинах симплекса стають достатньо малими. Недоліком цього методу є велика кількість ітерацій та він не завжди забезпечує розв’язок задачі.

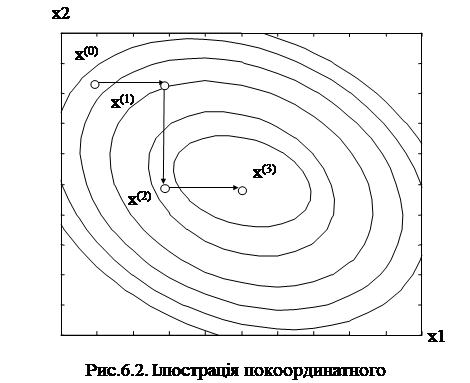
Ідея методу покоординатного спуску полягає в тому, що спочатку робиться пробний крок у напрямі, який паралельний до однієї з координатних осі і обчислюється значення цільової функції. Якщо значення цільової функції зменшується, то рух продовжується далі в цьому ж напрямку, а якщо функція збільшується, то ми повертаємося назад і робимо пробний крок у іншому напрямку. Цей процес продовжуємо до тих пір, поки не буде знайдена оптимальна точка (рис. 6.2). Особливість цього методу полягає в тому, що пошук оптимуму проводиться виключно паралельно координатним осям. На початку пошуку вибирається великий крок і перевіряється значення функції за всіма напрямками. Якщо буде зростання функції за всіма напрямками, то необхідно зменшити крок.

Недоліком цього методу є обмежені можливості під час пошуку оптимуму. Метод застосовують тоді, коли залежність між змінними х₁, х₂,…, х_n практично відсутня.

Ідея випадкового пошуку полягає в тому, що вибір напрямку руху здійснюється випадково. Якщо цільова функція зменшується, то рух у вибраному напрямку продовжується, а в протилежному випадку необхідно повернутися на один крок назад і знову випадково обрати напрямок пошуку і т.д.

Усі випадкові методи пошуку реалізуються за ітераційною формулою:

де k – номер ітерації;

ξ,^(k) – випадкова величина.

Популярність методів випадкового пошуку пояснюється їх простотою та широкими можливостями для користувачів самому модифікувати методи.

Порядок виконання роботи

1. Скласти схему алгоритму та програму оптимізації функції методом нульового порядку. Вихідні дані брати з табл.6.3 у відповідності до варіанта.

2. Достовірність отриманих результатів перевірити, використовуючи математичний пакет MathCAD.

3. Зробити висновки. Оформити звіт.

Таблиця 6.3. Варіанти завдань

Варіант	Цільова функція	Точність рішення	Метод оптимізації
1			Хука-Дживса
2			Покоординатного спуску
3			Нелдера-Мiда
4			Хука-Дживса
5			Покоординатного спуску
6			Нелдера-Мiда

*Вибрати початкові параметри в залежності від особливостей методу й обраної функції.

Склад звіту:

1.     Теоретичні відомості.

2.     Завдання.

3.     Блок-схема та лістинг програми.

4.     Результати оптимізації за розробленою програмою.

5.     Результати дослідження у MathCAD.

6.     Висновки.

Контрольні запитання

1. Класифікація методів безумовної оптимізації функцій багатьох змінних.

2. Особливості методів нульового порядку оптимізації багатомірних функцій.

3. Суть методів покоординатного спуску, Хука-Дживса та Нелдера-Міда.

Список використаної літератури:

1.   Методичні вказівки до виконання лабораторних робіт з курсу: «Методи оптимізації» для студентів 5-го курсу денної форми навчання спеціальності 7.091401 «Системи управління і автоматики» // fliphtml5.com/oktx/basic

2.    Методи оптимізації складних систем. Навчальний посібник. І.В.Кузьмін, М.М.Биков, С.М.Москвіна. – Вінниця: ВДТУ, 2003. – 164 с.

3.    Банди Б. Методы оптимизации. Вводный курс. – М.:”Радио и связь”, 1988. – 128 с.

4.    Дегтярев Ю.И. Методы оптимизации: учебное пособие. – М.: Советское радио, 1980. – 272 с.

5.    Ашманов С.А., Тимохов А.В. Теория оптимизации в задачах и упражнениях. – М.: Наука, 1991. – 448 с.

6.    Полак Е. Чисельні методи оптимізації. – М.: Мир, 1974.

7.    Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. – М.: Наука, 1986.