Тема 4. Ділова фінансова аналітика

4.1. Значення і теоретичні засади проведення фінансових аналітичних розрахунків.

4.2. Статистичне забезпечення ділового фінансового аналізу діяльності підприємств:

4.2.1. Абсолютні статистичні величини

4.2.2. Відносні статистичні величини

4.2.3. Середні величини

4.3. Рекомендації щодо застосування на практиці узагальнюючих статистичних показників

4.1. В сучасних умовах господарювання дедалі важливішого значення набуває ділова фінансова аналітика бізнесу. Актуальність даного питання полягає у тому, що розвиток ринкових відносин, нестабільність середовища, зростання вартості капіталу зумовлюють потребу такого аналізу з метою ефективного управління компанією.

В процесі аналізу фінансово-господарської діяльності підприємства можна використовувати традиційні (логічні) методи, графічні, експертні, економіко-математичні методи та моделі та інші.

Не зважаючи на велику кількість таких методів, існує проблема їх адаптації та застосування для окремого суб’єкта господарювання з врахуванням специфічних особливостей конкретних сфер економіки. Тобто проблема полягає у застосуванні на практиці єдино правильної методики для формулювання адекватних висновків та можливості порівняння отриманих результатів.

Фінансовий аналіз на підприємстві, як правило, зводиться до оцінки його фінансового стану за такими основними напрямами: аналіз фінансової стійкості, ліквідності та платоспроможності, фінансових результатів та рентабельності. Спочатку аналізується їх структура та динаміка за видами діяльності, проводиться факторний аналіз валового прибутку, аналіз операційних витрат та доходів. При цьому, глибина та системність оцінки стану фінансів підприємства, можливостей та загроз для бізнесу, у значній мірі залежать від вмілого застосування у діловій фінансовій аналітиці економіко-статистичних методів. Лише на їх основі можна правильно оцінити місце компанії в економічній системі країни та можливості її розвитку в майбутньому.

4.2.1. Абсолютні величини – статистичні величини, що відображують розміри (обсяг, рівень) суспільних явищ у одиницях ваги, довжини, площини, вартості тощо і відповідають на запитання «скільки?». Абсолютні статистичні величини – завжди числа іменовані, тобто вони мають певний розмір, певні одиниці виміру.

Найбільш поширені одиниці виміру (її вибір визначається суттю абсолютних величин, якостями явища, що аналізується, або завданнями обстеження):

– натуральні – відображують розмір речей, предметів, здебільшого відповідають природним аби споживчим властивостям предмета і виражаються у фізичних мірах, тобто у мірах ваги, об'єму, довжини, площі тощо. (Такі одиниці виміру використовують, наприклад, для характеристики обсягу виробництва різних видів продукції, продажу товарів, потужності електростанцій тощо. Так, видобуток вугілля, нафти, руди вимірюється у тонах, газу – у м³, виробництво електроенергії – у кВт/год., тканини – у метрах погонних та квадратних тощо).

– вартісні або грошові одиниці – узагальнюючи облікові дані навіть на рівні окремого суб’єкта господарювання, а тим паче на рівні видів економічної діяльності чи економіки в цілому, неможливо обмежитись лише натуральними одиницями. За одиницю беруть національну валюту, валютні еквіваленти на зразок євро, валюту інших держав;

– трудові – використовують для обліку витрат живої праці на виробництво продукції або виконання якоїсь роботи (це людино-години, людино-дні);

– часу – використовують у деяких випадках для обліку середньої тривалості життя людини (роки), строку служби будинків, споруд (роки), електролампочок (години) тощо;

– самі одиниці сукупності явищ (речей, предметів) – своєрідна одиниця виміру – кожна річ, предмет, явище, випадок є одночасно і одиницею сукупності, і одиницею виміру – використовують для визначення загальної чисельності сукупності або окремих її частин.

Абсолютні величини поділяють на два види:

– індивідуальні – виражають розміри кількісних ознак у окремих одиниць сукупності (заробітна плата окремого працівника, статутний фонд певного банку, товарообіг окремого магазину тощо). Індивідуальні абсолютні величини отримують у процесі статистичного спостереження, де вони реєструються у формулярах спостереження. Це величини які мають велике значення у статистичному обстеженні, оскільки є базою для загальних абсолютних величин при групуванні за кількісною ознакою. Вони ж є основою для віднесення кожної одиниці сукупності до тієї чи іншої групи;

– загальні – це вже узагальнені статистичні показники, результати зведення та групування. Вони виражають розміри, обсяг, величину тієї чи іншої ознаки у всіх одиниць досліджуваної сукупності або чисельність одиниць в цілому (або окремих її частин).

Абсолютні статистичні величини мають велике значення в статистиці – це основа для всіляких статистичних розрахунків, аналізу, розробки державних планів тощо (характеризують наявність усіх видів ресурсів – матеріальних, грошових, трудових; розміри виробництва усіх видів продукції). Але, щоб мати точне уявлення про міру зміни явищ, треба ці явища зіставити, адже усе пізнається у співставленні, у співвідношенні.

4.2.2. Абсолютні статистичні величини мають незаперечне значення в системі управління, проте поглиблений соціально-економічний аналіз фактів потребує різного роду порівнянь. Порівнюються значення статистичних показників у часі (за одним об'єктом), у просторі (між об'єктами), співвідносяться різні ознаки одного й того самого об'єкта.

Відносна величина – числова міра співвідношення двох порівнюваних статистичних величин. Тобто, цей узагальнений показник є результат ділення однієї величини на іншу величину. При обчисленні відносних величин слід мати на увазі, що:

– чисельник – звітна, фактична величина - показник, який вивчається. Зіставляючи звітну величину з базисною, визначають, у скільки разів порівнювана величина є більшою чи меншою від базисної;

– знаменник - база порівняння (основа, базисна величина) – величина, з якою порівнюють, править за своєрідний вимірювач.

Відносні величини мають дуже важливу особливість – вони абстрагують варіації абсолютних величин і дозволяють порівнювати такі явища, абсолютні розміри яких безпосередньо порівняти не можна.

Відносні величини утворюються в результаті співставлення однойменних та різнойменних величин:

1. Якщо зіставляються однойменні абсолютні величини, то отримують неіменовані відносні величини. Залежно від того, до якого значення прирівнюється база порівняння, частку від ділення можна виразити у:

– коефіцієнтах – значення основи (бази) порівняння прийнято за одиницю, то відносна величина (наслідок порівняння) показує, в скільки разів досліджуване значення більше (менше) від бази порівняння. Розрахунок відносних величин у вигляді коефіцієнтів доцільно застосовувати, якщо порівнювана величина є більшої від тієї, з якою її порівнюють;

– відсотках (%) – значення бази (основи) порівняння приймається за 100, відсоткове вираження відносних величин є найпоширенішим в практиці економічної роботи;

- промілях (‰) – база дорівнює 1000. Розрахунок відносних величин у вигляді проміле доцільно застосовувати, якщо результат ділення є надмірно малим в порівнянні з прийнятим у пояснювальній записці порядком подання даних, або висновок, що формується на основі результату є не коректним чи не етичним.

2. Якщо зіставляються різнойменні величини то відносні величини виражаються іменованими числами, назва яких складається з назв співставної і базисної величин (наприклад, густота населення осіб/км²).

В залежності від змісту, тобто від того, що саме та які співвідношення виражають відносні величини, їх можна поділити на види:

1. Динаміки (зміна соціально-економічного явища в часі) – характеризують ступінь зміни абсолютного або середнього рівня явища у звітному періоді у порівнянні з базисним, виражають ступінь зміни явищ у часі, характеризують напрям і швидкість зміни явищ у часі, темпи їх розвитку. Обчислюються як відношення рівня звітного періоду до рівня будь-якого іншого, прийнятого за базу. Залежно від характеру бази порівняння розрізняють два види відносних величин динаміки:

– ланцюгові – зі змінною базою порівняння, характеризують швидкість зміни показника від одного періоду до іншого;

– базисні – зі сталою базою порівняння, характеризують поступове віддалення цього самого показника від періоду, який взято за базу порівняння.

Вибір бази порівняння для базисних відносних величин має суттєве значення. За базу порівняння слід брати дані за роки, що найважливіші для розвитку досліджуваного процесу.

2. Планового завдання – показує, у скільки разів планова величина того чи іншого показника перевищує фактичну його величину в базисному періоді.

3. Виконання плану (договірних зобов'язань) – показує, у скільки разів фактична величина того чи іншого показника перевищує або менша за його планову величину. Обчислюється діленням фактичного рівня (обсягу виконаних зобов'язань) на запланований (обсяг зобов'язань, передбачених договором) за один і той же період. Обчислений в такий спосіб показник характеризує ступінь виконання підприємством своїх договірних зобов'язань).

4. Структури – характеризують склад сукупності, питому вагу складових частин цілого в їх загальному підсумку (статистичні сукупності структуровані, у них завжди можна виявити певні складові). Розраховують як відношення абсолютної величини кожного складового елемента до абсолютної величини всієї сукупності, тобто як відношення частини до цілого. Скільки складових, стільки відносних величин структури. Кожну з них окремо називають часткою, або питомою вагою, виражають простим чи десятковим дробом або відсотком. Наприклад, певна частина сукупності становить 1/4, або 0,25, або 25% загального обсягу сукупності (тобто, виражається у коефіцієнтах або у відсотках, переважно у відсотках). Відносні величини структури адитивні. Сума всіх часток дорівнює одиниці чи 100% відповідно.

За допомогою відносних величин структури можна оцінити структурні зрушення, тобто зміни у складі сукупності за певний період часу. Така оцінка ґрунтується на порівнянні часток за два періоди. Аналогічно можна порівняти структуру різних за обсягом сукупностей. Різницю між відповідними частками двох сукупностей називають відсотковим пунктом (в. п.).

5. Координації – поглиблений аналіз структури передбачає оцінювання співвідношень, пропорцій між окремими складовими одного цілого - показує, скільки одиниць однієї частини сукупності припадає на 1, 100 і 1000 одиниць іншої, узятої за базу порівняння (у скільки разів порівнювальна частина сукупності більша або менша частини, що приймається за базу порівняння. Виражається або у коефіцієнтах, або у відсотках (або у вигляді іменованих чисел).

6. Порівняння (порівняння в просторі, просторових порівнянь) – це співвідношення однойменних абсолютних величин, що належать різним об'єктам за один і той же період часу. Виражаються у коефіцієнтах та іноді у відсотках (найчастіше це регіональні чи міжнародні порівняння показників економічного розвитку або життєвого рівня. Вибір бази порівняння довільний. Головне, щоб методика розрахунку показників, що порівнюються, була однаковою).

7. Порівняння зі стандартом (певним еталоном) – нормативом, стандартом, оптимальним рівнем. Такими відносними величинами порівняння є виконання договірних зобов'язань, використання виробничих потужностей, додержання норм витрат електроенергії тощо. Будь-яке відхилення відносної величини від І чи 100% свідчить про порушення оптимальності процесу. Для показників, які не мають визначеного еталона (захворюваність, злочинність тощо), базою порівняння може бути максимальне чи мінімальне значення або середня по сукупності в цілому.

8. Інтенсивності – характеризують ступінь поширення досліджуваного явища у первинному середовищі, розвиток явища в певному просторі. Відносні величини інтенсивності завжди є відношенням двох різнойменних величин, а саме у чисельнику – величина явища (показник), поширення якого вивчають, а у знаменнику – величина того середовища, в якому розвивається (поширюється) це явище. Показує скільки одиниць однієї сукупності припадає на одиницю іншої сукупності. На відміну від інших відносна величина інтенсивності завжди є іменованою.

4.2.3. Середня величина – це узагальнюючий показник, який характеризує однорідну сукупність явищ за якою-небудь кількісною варіаційною ознакою в даних умовах місця і часу. Тільки за допомогою середньої можна охарактеризувати сукупність за кількісною варіаційною ознакою.

При обчисленні середніх у соціально-економічних дослідженнях необхідно чітко усвідомити визначальну властивість сукупності та логіко-математичну суть – логічну формулу – показника. Наприклад, логічна формула середнього вкладу в банк:

.

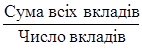Чисельник логічної формули середньої являє собою обсяг значень (визначальну властивість) ознаки, що варіює, а знаменник – обсяг сукупності. Як правило, визначальна властивість – це реальна абсолютна чи відносна величина, яка має самостійне значення в аналізі.

У кожному конкретному випадку для реалізації логічної формули використовується певний вид середньої, зокрема:

а) середня арифметична;

б) середня гармонійна;

в) середня геометрична;

г) середня квадратична і т. д.

Залежно від характеру первинної інформації середня будь-якого виду може бути:

– простою;

– зваженою.

Позначається середня символом (риска над символом означає осереднення індивідуальних значень) і вимірюється в тих самих одиницях, що й ознака.

Розглянемо найбільш поширені на практиці види середньої:

1. Середня арифметична

Оскільки для більшості соціально-економічних явищ характерна адитивність обсягів (виробництво цукру, витрати палива тощо), то найпоширенішою є арифметична середня, яка обчислюється діленням загального обсягу значень ознаки на обсяг сукупності. За первинними, не згрупованими даними обчислюється середня арифметична проста:

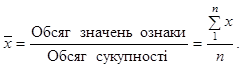
Моментні показники замінюються середніми як півсума значень на початок і кінець періоду. Якщо моментів більш ніж два, а інтервали часу між ними рівні, то в чисельнику до півсуми крайніх значень додають усі проміжні, а знаменником є число інтервалів, яке на одиницю менше від числа значень ознаки. Таку формулу називають середньою хронологічною:

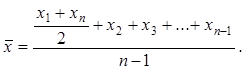
Наприклад, на фірмі залишки обігових коштів на початок кожного місяця І кварталу становили, млн грн.: січень – 70, лютий – 82, березень – 77, квітень – 80. Середньомісячний залишок обігових коштів, млн грн.:

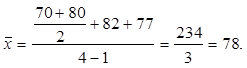
У великих за обсягом сукупностях окремі значення ознаки (варіанти) можуть повторюватись. У такому разі їх можна об’єднати в групи (j = 1, 2, ..., m), а обсяг значень ознаки визначити як суму добутків варіант х_j на відповідні їм частоти f_j, тобто як . Такий процес множення у статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами – вагами. Сама назва «ваги» відбиває факт різновагомості окремих варіант. Значення ознаки осереднюються за формулою середньої арифметичної зваженої:

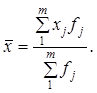
Середня може не збігатись з жодним значенням ознаки, але це типовий рівень значення ознаки в сукупності.

2. Середня гармонійна

При розрахунку середньої з обернених показників використовують середню гармонійну. Припустимо, що придбано товару в двох продавців на одну й ту саму суму — на 1 грн., але за різною ціною: по 3 грн. за 1 кг у першого продавця і по 2 грн. — у другого. Як визначити середню ціну покупки? Середня арифметична (3 + 2) : 2 = 2,5 грн. за 1 кг нереальна, оскільки за такою ціною на 2 грн. можна придбати 2 : 2,5 = 0,8 кг товару. Насправді придбано товару в першого продавця (1 : 3) = 0,33 кг, у другого — (1 : 2) = 0,50 кг, тобто разом 0,33 + 0,50 = 0,83 кг, а середня ціна становить 2 : 0,83 = 2,4 грн.

Описаний порядок розрахунку називають середньою гармонійною простою. У нашому прикладі

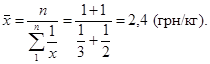
За умови, що в першого продавця придбано товару на 150 грн., а в другого – на 300 грн., середня ціна 1 кг, грн.:

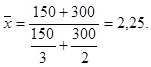
Цей розрахунок зроблено за формулою середньої гармонійної зваженої:

,

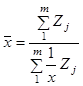де Z_j = x_j f_j — обсяг значень ознаки (у нашому прикладі – вартість).

У разі, коли осереднювана ознака є відношенням між логічно пов’язаними величинами (наприклад, відносна величина інтенсивності, структури тощо), постає питання про вибір виду середньої. Основою вибору є логічна формула показника. Так, рентабельність реалізації обчислюється відношенням:

Нехай рентабельність реалізації двох видів продукції малого підприємства становить, %: виробу А — 12, виробу В — 7. Прибуток від реалізації цих виробів дорівнює відповідно 240 і 210 тис. грн. Спроба визначити середню рентабельність як арифметичну не відповідає логічній формулі, така середня позбавлена реального економічного змісту. Для того щоб зберегти зміст, треба передусім визначити обсяг реалізації кожного виду продукції:

У цьому разі розрахунок середнього рівня рентабельності обох видів продукції відповідає формулі середньої гармонічної:

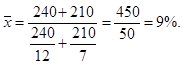
Отже, формула середньої – це лише математична модель логічної формули показника. Основний методологічний принцип вибору виду середньої – забезпечити логіко-змістовну суть показника.

4.3. Ми познайомились з найбільш простими узагальненими показниками і можемо зробити такі висновки:

1) абсолютні величини необхідні для керівництва, управління та планування видів економічної діяльності національної економіки;

2) абсолютні величини доцільно застосовувати разом з відносними, оскільки останні з найбільшою чіткістю та наочністю характеризують міру змін явищ;

3) засвоєння використання абсолютних та відносних величин дає змогу значно збагатити та поглибити аналіз тих чи інших економічних явищ;

4) дані лише про абсолютні розміри суспільних явищ, не дивлячись на колосальне їх наукове і практичне значення, не дозволяють у багатьох випадках охарактеризувати всі сторони досліджуваного об'єкта. Так, лише відомості про обсяг промислового виробництва в абсолютних вимірах не дають ще достатньої уяви про рівень економічного розвитку тієї чи іншої країни, бо, як відомо, останній визначається не самим обсягом виробництва, а обсягом виробництва в розрахунку на душу населення. Тому для визначення рівня економічного розвитку країни необхідно обсяг річної промислової продукції порівняти з чисельністю населення (з територією);

5) майстерність економіста-дослідника полягає у творчому взаємному доповненні показників двох систем. Так, наприклад, якщо торгова площа першого магазину збільшена зі 100 м² до 200 м², то це означає, що вона зросла в два рази, але коли торгова площа другого магазину зросла з 600 м²до 900 м², то її загальне збільшення складає 1,5 рази. Може виникнути справедливе питання: який з магазинів працював краще в напрямку нарощування виробничих площ?

Відносний приріст виробничої площі в першому магазині складає 100%, другому – 50%. Однак за кожним відсотком приросту стоять різні абсолютні обсяги приросту: в першому – 100 м², другому – 300 м² торгової площі. Допомогти тут може такий показник, як абсолютне значення одного відсотка приросту. В першому магазині він склав 1 м², а в другому – 6 м². Таким чином, хоч нарощування виробничих площ в першому магазині відбувалось швидше, внесок другого магазину в розширення торгівлі був вагомішим;

6) розрахунок відносних величин на основі абсолютних даних не є складним. Вимагає дотримування певних послідовностей розрахунок відносних величин виконання плану, коли саме планове завдання виражене у відносних величинах;

7) головна умова наукового використання середньої полягає в тому, що середні характеристики повинні вираховуватись на основі масового узагальнення фактів. Тільки тоді вони відображають суть явища, на значення якого не впливають одиничні фактори. Ця умова пов’язує статистичні середні із законом великих чисел;

8) важливою умовою застосування середніх в статистиці є якісна однорідність всіх одиниць сукупності. Не можна обчислювати середню з неоднорідної сукупності, окремі елементи якої підпорядковані різним законам розвитку по відношенню до осереднюванї ознаки.

9) середня величина тільки тоді відобразить типовий розмір ознаки та її загальні риси, якщо це загальне реально існує, всі елементи якого якісно однорідні і типові;

10) при використанні середніх потрібно пам’ятати, що середні величини не можуть і не повинні підміняти індивідуальні показники, а доповнюватись вивченням кращих і гірших одиниць сукупності.

Отже, статистичні методи в економічних дослідженнях потребують їх комплексного і творчого використання.

Питання для самоперевірки знань

1. До якого виду вимірників абсолютних величин належить показник обсягу виробництва валової продукції по підприємству ?

трудових;

натуральних;

умовно-натуральних;

вартісних.

2. До якого виду відносних величин належить показник виходу телят на 100 корів ?

інтенсивності;

структури;

порівняння;

координації.

3. У яких одиницях виражаються відносні показники, коли базова величина приймається за 1000 ?

відсотках;

коефіцієнтах;

проміле;

продециміле.

4. Які з перелічених величин характеризують відношення між однойменними показниками ?

відносні величини інтенсивності;

відносні величини координації;

відносні величини структури;

інтегровані відносні величини.

5. Які з перелічених величин характеризують підношення між різнойменними показниками ?

відносні величини виконання плану;

відносні величини структури;

відносні величини динаміки;

відносні величини інтенсивності.

6. Яка відносна величина характеризує відношення планового показника до іншої величини, прийнятої за базу порівняння?

відносна величина виконання плану;

відносна величина порівняння;

відносна величина координації;

відносна величина планового завдання.

7. Яка відносна величина характеризує зміну явищ і процесів у часі?

відносна величина структури;

відносна величина порівняння;

відносна величина динаміки;

відносна величина інтенсивності.

8. Яка відносна величина характеризує співвідношення між складовими частинами цілого?

відносна величина координації;

відносна величина структури;

відносна величина порівняння;

відносна величина інтенсивності.

9. Яка величина характеризує склад того чи іншого суспільного явища ?

відносна величина порівняння;

відносна величина структури;

відносна величина координації;

відносна величина динаміки.

10. У якому з наведених прикладів обчислена відносна величина координації?

кількість автомобілів на початок року в одному підприємстві у відношенні до іншого підприємства становить 86 %;

щільність поголів’я корів на 100 га сільськогосподарських угідь у становить 27 голів;

на 100 робітників підприємства припадає 70 жінок;

частка зернових культур у загальній площі посіву становить 36 %.