Тема 2. Основи фінансових розрахунків

2.1. Основні поняття фінансових розрахунків

2.2. Нарахування по простих процентних ставках

2.3. Особливості нарахування складних процентів

2.1. Фінансові операції, що складають основу комерційних обчислень, мають давню історію. Саме в цих операціях і виявляється насамперед необхідність врахування часової цінності грошей. Незважаючи на те, що в основі розрахунків при аналізі ефективності позичково-кредитних операцій закладені найпростіші, на перший погляд, схеми нарахування відсотків, ці розрахунки різноманітні через різноманітність умов фінансових контрактів стосовно частоти і способів нарахування, а також варіантів надання і погашення позичок.

Проценти – абсолютна величина доходу від надання грошей в борг в будь-якій формі: видача позики, продаж товару в кредит, розміщення грошей на депозитному рахунку, облік векселя, покупка облігації і т.д.

Процентна ставка – відносна величина доходу за фіксований проміжок часу або відношення процентних грошей до суми боргу. Вона вимірюється у вигляді десяткового або звичайного дробу (з точністю до 1/16 або 1/32), або в %.

Період нарахування – часовий інтервал, до якого приурочена процентна ставка.

Нарощування – процес збільшення суми грошей в часі у зв’язку з додаванням процентів.

Дисконтування – визначення суми грошей від майбутнього до сучасного періоду, скидка.

Процентні ставки поділяють на декілька видів:

-          прості (при постійній базі нарахування);

-        складні (за базу приймають суму, отриману на попередньому етапі нарощування або дисконтування);

-        рекурсивні (проценти по ставці нарощування);

-        антисипативні (проценти по ставці дисконтування);

-        фіксовані (з вказаними розмірами в контракті);

-        плаваючі (база змінюється в часі);

Одним з найважливіших властивостей грошових потоків є їх розподіленість у часі. При аналізі щодо короткострокових періодів (до 1 року) в умовах стабільної економіки дана властивість робить відносно незначний вплив, яким часто зневажають. Визначаючи річний обсяг реалізації по підприємству, просто складають суми виторгу за кожний з місяців звітного року. Аналогічно надходять із усіма іншими грошовими потоками, що дозволяє оперувати їхніми підсумковими значеннями. Однак у випадку більше тривалих періодів або в умовах сильної інфляції виникає серйозна проблема забезпечення порівнянності даних. Та сама номінальна сума грошей, отримана підприємством з інтервалом в 1 і більше рік, у таких умовах буде мати для нього неоднакову цінність. Очевидно, що 1 млн. грн. на початку 2015 року був значно більше мільйона «зразка» 2017 і більше пізнього років. Як правило, у таких випадках роблять коректування звітних даних з урахуванням інфляції. Але проблема не зводиться тільки до обліку інфляції. Одним з основних принципів фінансової грамотності є визнання тимчасової цінності грошей, тобто залежності їхньої реальної вартості від величини проміжку часу, що залишається до їхнього одержання або витрати. В економічній теорії ця властивість називається позитивною тимчасовою перевагою.

Поряд з інфляційним знецінюванням грошей існує ще як мінімум три найважливіші причини даного економічного феномена. По-перше, «сьогоднішні» гроші завжди будуть цінніші «завтрашніх» через ризик неотримання останніх, і цей ризик буде тим вище, чим більше проміжок часу, що відокремлює одержувача грошей від цього «завтра». По-друге, маючи у своєму розпорядженні грошові засоби «сьогодні», економічний суб'єкт може вкласти їх у яке-небудь дохідне підприємство й заробити прибуток, у той час як одержувач майбутніх грошей позбавлений цієї можливості. Розстаючись із грішми «сьогодні» на певний період часу (допустимо, даючи їх у борг на 1 місяць), власник не тільки піддає себе ризику їхнього неповернення, але й несе реальні економічні втрати у формі неодержаних доходів від інвестування. Крім того знижується його платоспроможність, тому що будь-які зобов'язання, одержувані їм замість грошей, мають більше низьку ліквідність, чим «живі» гроші. Тобто в кредитора зростає ризик втрати ліквідності, і це третя причина позитивної тимчасової переваги. Природно, більшість власників грошей не згодні безкоштовно приймати на себе настільки істотні додаткові ризики. Тому, надаючи кредит, вони встановлюють такі умови його повернення, які на їхню думку повністю відшкодують їм всі моральні й матеріальні незручності, що виникають у людини, що розстається (нехай навіть і тимчасово) із грошовими знаками.

Необхідність врахування фактора часу слідує із суті фінансування, кредитування та інвестування і виражається в принципі нерівноцінності грошей, які відносяться до різних моментів часу. Вплив фактора часу особливо посилюється в період інфляції. Не менш важливим є і принцип фінансової еквівалентності – рівності фінансових зобов’язань сторін, які беруть участь в операції. Він дозволяє змінити умови контракту без порушення прийнятих зобов’язань. Вищезгадані два принципи не можуть бути реалізовані без того чи іншого способу нарощування процентів або їх дисконтування.

Для подальшого вивчення теми введемо такі позначення:

I – проценти за весь термін позики;

P – початкова сума боргу;

S – кінцева сума (нарощувана)

i – ставка нарощування процентів (десятковий дріб);

n – термін позики (в роках);

d – облікова процентна ставка;

j – номінальна процентна ставка;

ν_n – множник нарощування по складних процентах;

p – ціна одиниці продукції.

2.2. Нарощування по простих процентах використовують при наданні короткострокової позики (до 1 року), або у випадку, коли проценти не додаються до суми боргу, а періодично виплачуються. Під нарощуваною сумою позики розуміють її початкову суму з нарахованими процентами до кінця терміну нарахування. Користуючись вищенаведеними позначеннями:

Вираз (1+ni) називають множником нарощування по простих процентах. Збільшення процентної ставки або терміну в k разів однаково впливає на множник нарощування. Він збільшується в разів.

Оскільки процентна ставка, як правило, встановлюється в розрахунку за рік, то при терміні позики менше року:

де t – кількість днів позики;

K – часова база нарахування процентів (360 днів – 12 місяців по 30 днів, або 365 чи 366 днів).

У залежності від сполучення кількості днів позики та виду часової бази, існують такі способи розрахунків:

1) Англійська практика: t і K виміряні точно. Метод називається вирахуванням точних відсотків з фактичним терміном операції;

2)    Французька практика: t виміряна точно, а K – наближено. Метод називається нарахуванням звичайних (комерційних) процентів з фактичним терміном операції. У цьому випадку проценти виходять більшими, ніж у першому, тому що знаменник дробу дорівнює 360, а не 365 (366). Зазвичай по такому принципу ведуться банківські операції;

3)    Німецька практика: t і K виміряні приблизно. Метод називається нарахуванням звичайних (комерційних) процентів з наближеним терміном операції. Застосовується для деяких розрахунків з населенням.

Короткострокові зобов’язання можуть погашатись і з допомогою часткових платежів. При цьому використовують два методи:

ü актуарний (термін позики більше 1 року):

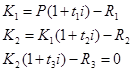
ü правило торговця (термін менше 1 року):

де Rj – часткові платежі;

tj – часові інтервали;

Kj – суми боргу.

Якщо загальний термін позики охоплює два суміжних календарних роки, і є необхідність в поділі суми процентів між ними, то загальна сума нарахованих простих процентів складе:

де n1,n2 – частини терміну позики, що припадають на кожен календарний рік.

Якщо сума, на яку нараховують проценти, змінюється у часі (поповнення рахунку, або зняття грошей), то використовують формулу:

де Rj - залишок грошей на рахунку в момент j після чергової зміни;

nj – термін зберігання грошей (в роках) до нової зміни залишку засобів.

2.3. З позицій фінансового менеджменту використання складних відсотків є більше кращим, тому що визнання можливості власника в будь-який момент інвестувати свої засоби з метою одержання доходу є наріжним каменем всієї фінансової теорії. При використанні простих відсотків ця можливість часто не враховується, тому результати обчислень виходять менш коректними. Проте при короткострокових фінансових операціях як і раніше широко застосовуються обчислення простих відсотків. Деякі математики вважають це прикрим пережитком, що залишився з тих пір, коли у фінансистів не було під рукою калькуляторів і вони були змушені прибігати до більш простих, хоча й менш точних способів розрахунку. Але можливе інше пояснення цього факту. При тривалості операції менш 1 року (n < 1) нарахування простих відсотків забезпечує одержання результатів навіть більше вигідних для кредитора, ніж використання складних відсотків. Вище вже відзначалася закономірність вибору банками саме таких, більше вигідних для кредитора, способів. Тому було б наївно недооцінювати обчислювальні потужності сучасних банків та інтелектуальний потенціал їхніх співробітників, думаючи, що вони використають грубі методи розрахунків тільки через їхню низьку трудомісткість. Важко уявити собі банкіра, хоча б на секунду забуваючого про власну вигоду.

В середньо і довгострокових фінансово-кредитних операціях, якщо проценти не виплачуються зразу, а додаються до суми боргу, застосовують складні проценти. База для їх нарахування не залишається постійною, а весь час збільшується. Якщо проценти на борг нараховуються і додаються до основної суми боргу лише 1 раз на рік, то:

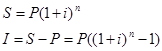
Якщо термін позики не дорівнює цілому числу років, то використовують змішаний метод нарахування процентів:

де n = a + b – термін позики;

a – ціле число років;

b – дробова частина року.

Для того, щоб співставити результати нарощування по різних процентних ставках, достатньо порівняти відповідні множники нарощування:

- для терміну менше року прості проценти більші за складні;

- для терміну більше року прості проценти менші за складні;

- для терміну 1 рік множники нарощування рівні між собою.

Важливою особливістю складних відсотків є залежність кінцевого результату від кількості нарахувань протягом року. Тут знову позначається вплив реінвестування нарахованих відсотків: база нарахування зростає з кожним новим нарахуванням, а не залишається незмінною, як у випадку простих відсотків.

Теоретично можна уявити ситуацію, коли нарахування складних відсотків відбувається настільки часто, що загальне його число в році прагне до нескінченості, тоді величина проміжку між окремими нарахуваннями буде наближатися до нуля, тобто нарахування стане практично безперервним. Така, на перший погляд гіпотетична ситуація, має важливе значення для фінансів і при побудові складних аналітичних моделей (наприклад при розробці масштабних інвестиційних проектів) часто застосовують безперервні відсотки. Безперервна процентна ставка (очевидно, що при безперервному нарахуванні мова може йти тільки про складні відсотки) позначається буквою δ (читається "дельта"), часто цей показник називають "сила росту".

Для безперервних відсотків не існує розходжень між процентною й дисконтною ставками – сила росту є універсальним показником. Однак, поряд з постійною силою росту може використатися змінна процентна ставка, величина якої міняється за заданим законом (математичної функції). У цьому випадку можна будувати дуже потужні імітаційні моделі, однак математичний апарат розрахунку таких моделей досить складний і не розглядається в конспекті лекцій, так само як і нарахування відсотків по змінній безперервній процентній ставці. 

Питання для самоперевірки знань

1. Англійська практика нарахування процентів – це

метод нарахування звичайних процентів з фактичним терміном операції;

метод нарахування звичайних процентів з подвійним терміном операції;

метод нарахування звичайних процентів з наближеним терміном операції;

метод нарахування точних процентів з фактичним терміном операції;

метод нарахування подвійних процентів з наближеним терміном операції;

2. Німецька практика нарахування процентів – це

метод нарахування звичайних процентів з фактичним терміном операції;

метод нарахування звичайних процентів з подвійним терміном операції;

метод нарахування звичайних процентів з наближеним терміном операції;

метод нарахування точних процентів з фактичним терміном операції;

метод нарахування подвійних процентів з наближеним терміном операції;

3. Французька практика нарахування процентів – це

метод нарахування звичайних процентів з фактичним терміном операції;

метод нарахування звичайних процентів з подвійним терміном операції;

метод нарахування звичайних процентів з наближеним терміном операції;

метод нарахування точних процентів з фактичним терміном операції;

метод нарахування подвійних процентів з наближеним терміном операції;

4. Проценти у фінансових розрахунках – це:

дохід, виражений у вигляді десяткового дробу;

абсолютна величина доходу від надання грошей у борг;

дохід, виражений у вигляді звичайного дробу;

втрати, виражені у вигляді звичайного дробу;

це – число у процентному форматі.

5. Види процентних ставок в залежності від бази нарахування:

постійна, складна;

проста, змінна;

проста, складна;

змінна, складна;

постійна, змінна.

6. Чим більше періодів нарахування процентів:

тим повільніше іде процес нарощування;

тим швидше іде процес нарощування;

процес нарощування не змінюється;

процес нарощування не починається;

процес нарощування передбачити не можна.

7. Реальна дохідність фінансової операції визначається:

з використанням реальної ставки процентів;

з використанням номінальної ставки процентів;

доходи мінус витрати;

з використанням ефективної ставки;

методом торговця.