ТЕМА 3.
ПОБУДОВА ТА ДОСЛІДЖЕННЯ ВИРОБНИЧОЇ ФУНКЦІЇ.
1. Поняття про
виробничу функцію.
2. Приклади виробничих функцій.
3.
Побудова та аналіз регресії попиту.
1. Поняття про виробничу функцію.
Виробнича функція – це функція, незалежна змінна якої набуває значення обсягу
ресурсу, який використовується для виробництва, а залежна змінна – значення
обсягів виготовленої продукції.
Виробничі функції охоплюють моделювання залежностей між
показниками виробничої діяльності, такими як обсяг випущеної продукції,
собівартість одиниці продукції, капітальні витрати, фондовіддача,
продуктивність праці та ін. При цьому в якості факторів можуть виступати
затрати праці, засобів виробництва та ін., а в якості показника – обсяг випуску
продукції, чистий дохід, ВВП та ін.
Залежно від кількості факторів, які включених в модель,
розрізняють однофакторні та багатофакторні виробничі функції (ВФ).
Загальний вигляд однофакторної виробничої функції :
![]() , (3.1)
, (3.1)
де а – вектор параметрів виробничої
функції;
![]() – незалежна змінна
(певний фактор виробництва);
– незалежна змінна
(певний фактор виробництва);
![]() – залежна змінна.
– залежна змінна.
Загальний вигляд багатофакторної виробничої функції:
![]() , (3.2)
, (3.2)
де а – вектор
параметрів виробничої функції;
![]() – незалежні змінні
(різні фактори виробництва);
– незалежні змінні
(різні фактори виробництва);
![]() – залежна змінна.
– залежна змінна.
Виробничі функції широко застосовується для аналізу і
прогнозування економічних явищ як на мікроекономічному, так і на
макроекономічному рівні.
Виробничі функції можуть бути як статичними (якщо параметри і
значення показника не залежать від часу), так і динамічними (якщо параметри і
значення показника залежать від часу, який як самостійна величина включається у
модель).
2. Приклади виробничих функцій.
Розглянемо приклади найбільш поширених виробничих функцій.
1. Логістична регресія
– використовується для прогнозування попиту на товари тривалого користування:
![]() , (3.3)
, (3.3)
де ![]() – забезпеченість
товаром;
– забезпеченість
товаром;
t – час;
![]() – насиченість ринку
товаром.
– насиченість ринку
товаром.
Попит на товари тривалого користування має таку тенденцію до
зміни: спочатку деякий час попит зростає, а потім коливається навколо сталої
величини.
2. Крива Енгеля –
використовується для
аналізу залежності між витратами на споживання та доходом:
![]() (3.4)
(3.4)
де ![]() – витрати на
споживання;
– витрати на
споживання;
![]() – дохід;
– дохід;
![]() ,
, ![]() .
.
Критична точка ![]() визначає рівень доходу,
нижче якого товар не буде куплений. Якщо дохід збільшується, то і збільшуються
витрати на споживання, але до певної межі
визначає рівень доходу,
нижче якого товар не буде куплений. Якщо дохід збільшується, то і збільшуються
витрати на споживання, але до певної межі ![]() , яка називається «межею насичення».
, яка називається «межею насичення».
3. Функція Лаффера –
використовується для характеристики залежності між податковою ставкою та
обсягом податкових надходжень:
![]() ,
, ![]() (3.5)
(3.5)
де ![]() – обсяг податкових
надходжень;
– обсяг податкових
надходжень;
![]() – податкова ставка.
– податкова ставка.
Існує оптимальний розмір податкової ставки (![]() ), якому відповідає максимальне значення обсягу податкових
надходжень. При відхиленні податкової ставки від оптимального значення в
сторону як збільшення, так і зменшення обсяг податкових надходжень різко
зменшується.
), якому відповідає максимальне значення обсягу податкових
надходжень. При відхиленні податкової ставки від оптимального значення в
сторону як збільшення, так і зменшення обсяг податкових надходжень різко
зменшується.
4. Виробнича функція
Кобба-Дугласа – використовується для аналізу залежності між затратами праці
і затратами капіталу на обсяг виробництва продукції:
![]() , (3.6)
, (3.6)
де ![]() – випуск валової продукції;
– випуск валової продукції;
![]() – затрати праці;
– затрати праці;
![]() – затрати капіталу
(вартість основних фондів);
– затрати капіталу
(вартість основних фондів);
![]() – параметри виробничої
функції.
– параметри виробничої
функції.
3. Побудова
та аналіз моделі регресії попиту.
3.1. Знаходження параметрів
регресії попиту
Нехай між ціною P та величиною попиту D існує
стохастична залежність у вигляді многочлена
другого порядку:
![]() , (3.7)
, (3.7)
де ![]() - невідомі параметри
регресії.
- невідомі параметри
регресії.
Для регресії у вигляді многочлена другого степеня система
нормальних рівнянь має такий вигляд:
![]()
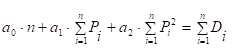 ,
,
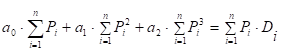 , (3.8)
, (3.8)
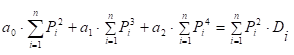 .
.
Розв’язавши систему рівнянь (3.8), отримаємо
оцінки параметрів регресії попиту.
3.2. Перевірка адекватності моделі
експериментальним даним
Для
перевірки адекватності прийнятої економетричної моделі експериментальним даним
скористаємось ![]() -критерієм Фішера, який полягає в наступному.
-критерієм Фішера, який полягає в наступному.
Розраховуємо
значення критерію за формулою:
![]() . (3.9)
. (3.9)
Знаходимо
табличне значення ![]() за заданою ймовірністю
за заданою ймовірністю
![]() та числом ступенів вільності
та числом ступенів вільності ![]() і
і ![]() , які визначаються за формулами:
, які визначаються за формулами:
![]() ,
, ![]() ,
(3.10)
,
(3.10)
де ![]() - кількість проведених спостережень;
- кількість проведених спостережень;
![]() - кількість факторів, які мають суттєвий вплив на показник.
- кількість факторів, які мають суттєвий вплив на показник.
Якщо виконується нерівність:
![]() >
>![]() , (3.11)
, (3.11)
то прийнята
економетрична модель вважається адекватною експериментальним даним і для неї
справедливі всі закономірності функціонування і розвитку, які характерні для
реального економічного явища. Тобто її можна використовувати для аналізу та
прогнозування індивідуальних ринків.
3.3. Вплив еластичності попиту на ринкові
обороти
Нехай відома
регресія попиту ![]() на певний вид товару
як функція від ціни товару
на певний вид товару
як функція від ціни товару ![]() :
: ![]() . Тоді товарообіг
. Тоді товарообіг ![]() у грошовому виразі
дорівнює добутку реалізованого попиту на ціну товару:
у грошовому виразі
дорівнює добутку реалізованого попиту на ціну товару:
![]() . (3.12)
. (3.12)
Дослідимо
зміни товарообігу в грошовому виразі залежно від зміни ціни на товар. Проведемо
дослідження зміни товарообігу ![]() залежно від значень
залежно від значень ![]() , тобто знайдемо проміжки зростання, спадання і точку
екстремуму товарообігу
, тобто знайдемо проміжки зростання, спадання і точку
екстремуму товарообігу ![]() . Для цього знайдемо похідну від
. Для цього знайдемо похідну від ![]() по
по ![]() :
:
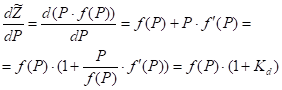 (3.13)
(3.13)
де ![]() - коефіцієнт
еластичності попиту.
- коефіцієнт
еластичності попиту.
Отже, товарообіг ![]() є функцією від коефіцієнта еластичності попиту
є функцією від коефіцієнта еластичності попиту
![]() . Залежно від знака
. Залежно від знака ![]() розрізняють три різних
варіанти еластичності попиту:
розрізняють три різних
варіанти еластичності попиту:
1. Якщо похідна
від товарообігу за ціною додатна ![]() >0, то при зростанні ціни Р зростає товарообіг
>0, то при зростанні ціни Р зростає товарообіг ![]() . Оскільки з економічного змісту f(P)>0, то
. Оскільки з економічного змісту f(P)>0, то ![]() буде більше нуля,
якщо
буде більше нуля,
якщо ![]() >0. Звідки випливає, що на проміжку, де товарообіг
зростає, коефіцієнт еластичності попиту
>0. Звідки випливає, що на проміжку, де товарообіг
зростає, коефіцієнт еластичності попиту ![]() >-1. З іншого боку, регресія попиту спадна і тому
>-1. З іншого боку, регресія попиту спадна і тому ![]() <0. Звідки випливає, що
<0. Звідки випливає, що ![]() <0.
<0.
Таким чином, на проміжку, де
товарообіг зростає, коефіцієнт еластичності попиту змінюється в межах від -1до
0.
В економіці прийнято називати попит нееластичним, якщо
коефіцієнт еластичності попиту змінюється в межах від -1 до 0.
Економічна інтерпретація. Зміна ціни на 1% викликає зміну попиту в
зворотному напрямку на ![]() %, де -1<
%, де -1<![]() <0, при цьому товарообіг у грошовому виразі зростає.
<0, при цьому товарообіг у грошовому виразі зростає.
2. Якщо ![]() <0, то з підвищенням ціни на товар відбувається
зниження товарообігу в грошовому виразі. Оскільки
<0, то з підвищенням ціни на товар відбувається
зниження товарообігу в грошовому виразі. Оскільки ![]() [
[![]() ] < 0, а
] < 0, а ![]() >0, то
>0, то ![]() <0. Звідки випливає, що
<0. Звідки випливає, що ![]() <-1.
<-1.
Якщо значення_коефіцієнта еластичності попиту для даної
ціни P менше –1, то попит при цій ціні
еластичний.
Економічна інтерпретація. При еластичному попиті зміна ціни товару
на 1% викликає зміну попиту в зворотному напрямку на ![]() %, де
%, де ![]() <-1. При цьому товарообіг у грошовому виразі зі зростанням
ціни спадає.
<-1. При цьому товарообіг у грошовому виразі зі зростанням
ціни спадає.
3. Якщо ![]() =0 для деякого проміжку цін, то на цьому проміжку
товарообіг залишається сталим.
=0 для деякого проміжку цін, то на цьому проміжку
товарообіг залишається сталим.
Якщо в деякій точці ![]() =0, то ця точка називається критичною. Причому, якщо при
переході через цю точку похідна
=0, то ця точка називається критичною. Причому, якщо при
переході через цю точку похідна ![]() змінює знак з
плюса на мінус, то при цій ціні товарообіг у грошовому виразі буде
максимальним. Коефіцієнт еластичності в цій точці дорівнює -1.
змінює знак з
плюса на мінус, то при цій ціні товарообіг у грошовому виразі буде
максимальним. Коефіцієнт еластичності в цій точці дорівнює -1.
3.4. Обґрунтування
оптимальної ціни за критерієм максимізації доходу
Визначимо проміжки зростання та спадання товарообігу.
Оскільки регресія попиту має вигляд многочлена другого порядку ![]() , то товарообіг для цієї регресії знаходиться за формулою:
, то товарообіг для цієї регресії знаходиться за формулою:
![]() .
(3.14)
.
(3.14)
Знайдемо похідну від товарообігу по ціні:
![]() . (3.15)
. (3.15)
З необхідної умови екстремуму ![]() =0 знайдемо критичні точки:
=0 знайдемо критичні точки:
![]() . (3.16)
. (3.16)
Наведене рівняння можна отримати також з умови:
![]() . (3.17)
. (3.17)
Знайдемо залежність коефіцієнта еластичності попиту від
ціни:
![]() (3.18)
(3.18)
3.5. Обґрунтування оптимальної ціни за критерієм
максимізації прибутку
Нехай собівартість продукції складається із
сталих затрат С та змінних затрат,
пропорційних обсягу випуску продукції VD (тут V – витрати
на одиницю продукції). У цьому випадку прибуток підприємства буде дорівнювати
різниці між товарообігом у грошовому виразі і собівартістю продукції, тобто:
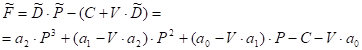 (3.19)
(3.19)
Знайдемо оцінку ціни, за якої прибуток буде максимальним.
Якщо в деякій точці F досягає екстремуму, то в цій точці похідна
дорівнює нулю.
Знайдемо критичні точки:
![]() , (3.20)
, (3.20)
тобто одержимо квадратне рівняння:
![]() . (3.21)
. (3.21)
Розв’язавши його, отримаємо два розв’язки:
![]() (3.22)
(3.22)
де дискримінант![]() . (3.23)
. (3.23)
Точку екстремуму знаходимо, дослідивши регресію
товарообігу. Припустимо, що це буде значення ![]() , тоді оптимальна кількість продукції, що випускається,
визначається за формулою:
, тоді оптимальна кількість продукції, що випускається,
визначається за формулою:
![]() ,
(3.24)
,
(3.24)
а максимальний прибуток:
![]() (3.25)
(3.25)
3.6. Прогнозування
на основі регресії попиту.
Підставивши у
відповідні рівняння прогнозне значення ціни, можна визначити прогнозні значення
обсягу попиту, товарообігу і прибутку.