ТЕМА 5. ВИРОБНИЧІ ФУНКЦІЇ.

1.   Поняття про виробничу функцію.

2.   Приклади виробничих функцій.

3.   Виробнича функція Кобба-Дугласа.

4.   Побудова та аналіз моделі виробничої функції Кобба-Дугласа.

5.   Основні характеристики виробничої функції Кобба-Дугласа.

6.   Геометрична інтерпретація основних характеристик виробничої функції Кобба-Дугласа.

1.   Поняття про виробничу функцію.

Виробнича функція – це функція, незалежна змінна якої набуває значення обсягу ресурсу, який використовується для виробництва, а залежна змінна – значення обсягів виготовленої продукції.

Виробничі функції охоплюють моделювання залежностей між показниками виробничої діяльності, такими як обсяг випущеної продукції, собівартість одиниці продукції, капітальні витрати, фондовіддача, продуктивність праці та ін. При цьому в якості факторів можуть виступати затрати праці, засобів виробництва та ін., а в якості показника – обсяг випуску продукції, чистий дохід, ВВП та ін.

Залежно від кількості факторів, які включених в модель, розрізняють однофакторні та багатофакторні виробничі функції (ВФ).

Загальний вигляд однофакторної виробничої функції :

, (5.1)

де а – вектор параметрів виробничої функції;

– незалежна змінна (певний фактор виробництва);

– залежна змінна.

Загальний вигляд багатофакторної виробничої функції:

, (5.2)

де а – вектор параметрів виробничої функції;

– незалежні змінні (різні фактори виробництва);

– залежна змінна.

Виробничі функції широко застосовується для аналізу і прогнозування економічних явищ як на мікроекономічному, так і на макроекономічному рівні.

Виробничі функції можуть бути як статичними (якщо параметри і значення показника не залежать від часу), так і динамічними (якщо параметри і значення показника залежать від часу, який як самостійна величина включається у модель).

2.   Приклади виробничих функцій.

Розглянемо приклади найбільш поширених виробничих функцій.

1. Логістична регресія – використовується для прогнозування попиту на товари тривалого користування:

, (5.3)

де – забезпеченість товаром;

t – час;

– насиченість ринку товаром.

Попит на товари тривалого користування має таку тенденцію до зміни: спочатку деякий час попит зростає, а потім коливається навколо сталої величини.

2. Крива Енгеля – використовується для аналізу залежності між витратами на споживання та доходом:

(5.4)

де – витрати на споживання;

– дохід;

, .

Критична точка визначає рівень доходу, нижче якого товар не буде куплений. Якщо дохід збільшується, то і збільшуються витрати на споживання, але до певної межі , яка називається «межею насичення».

3. Функція Лаффера – використовується для характеристики залежності між податковою ставкою та обсягом податкових надходжень:

, (5.5)

де – обсяг податкових надходжень;

– податкова ставка.

Існує оптимальний розмір податкової ставки (), якому відповідає максимальне значення обсягу податкових надходжень. При відхиленні податкової ставки від оптимального значення в сторону як збільшення, так і зменшення обсяг податкових надходжень різко зменшується.

4. Регресія попиту – використовується для аналізу індивідуального ринку:

, (5.6)

де – ціна продукції;

– попит на цю продукцію.

Якщо відомі параметри виробничої функції попиту, то можна розглянути функцію товарообігу:

, (5.7)

Досліджуючи дані функції, можна знайти ціну, яка забезпечує максимальний попит, та ціну, яка забезпечує максимальний прибуток.

3.   Виробнича функція Кобба-Дугласа.

Виробнича функція Кобба-Дугласа задається формулою:

, (5.8)

де – випуск валової продукції;

– затрати праці;

– затрати капіталу (вартість основних фондів);

– параметри виробничої функції.

4.   Побудова та аналіз моделі виробничої функції Кобба-Дугласа.

Оцінка параметрів виробничої функції Кобба-Дугласа здійснюється за допомогою методу найменших квадратів.

Виведемо формули для знаходження параметрів виробничої функції Кобба-Дугласа. Прологарифмуємо вираз (5.8) :

. (5.9)

Введемо замінну змінних:

; ; ; . (5.10)

Отримаємо множинну лінійну регресію:

. (5.11)

Запишемо систему нормальних рівнянь:

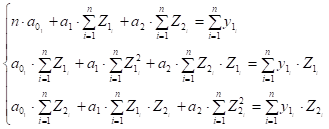(5.12)

Розв’язавши систему, наприклад, методом оберненої матриці або методом Крамера, знайдемо параметри виробничої функції Кобба-Дугласа.

За критерієм Фішера проводять перевірку на адекватність побудованої моделі статистичним даним. Алгоритм описаний у попередній темі.

5.   Основні характеристики виробничої функції Кобба-Дугласа.

Основні характеристики виробничої функції Кобба-Дугласа:

1. Середня продуктивність праці – показує середню кількість випущеної продукції на одиницю затраченої праці:

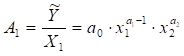. (5.13)

2. Гранична продуктивність праці – показує, скільки додаткових одиниць випущеної продукції приносить додаткова одиниця затраченої праці.

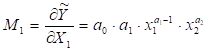. (5.14)

3.   Еластичність випуску продукції за затратами праці – показує, на скільки відсотків збільшується випуск продукції при збільшенні затрат праці на 1%.

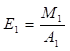; ; . (5.15)

4. Середня капіталовіддача (фондовіддача) – показує середню кількість випущеної продукції на одиницю затраченого капіталу:

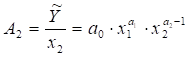. (5.16)

5. Гранична капіталовіддача (фондовіддача) – показує, скільки додаткових одиниць випущеної продукції приносить додаткова одиниця затраченого капіталу:

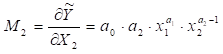. (5.17)

6. Еластичність випуску продукції за обсягом капіталу, яка показує на скільки відсотків збільшується обсяг випуску продукції при збільшенні затрат капіталу на 1%:

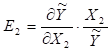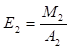; ; . (5.18)

7. Сумарна еластичність за витратами (праці і капіталу), яка показує, на скільки відсотків збільшується обсяг випуску продукції при одночасному пропорційному збільшення обсягів затраченої праці на 1% і капіталу на 1%:

. (5.19)

8. Капіталоозброєність праці :

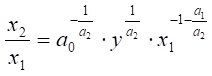. (5.20)

Виробнича функція дозволяє розраховувати потребу в одному з ресурсів при заданому обсягу виробництва та величині другого ресурсу.

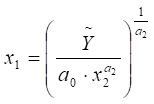(5.21)

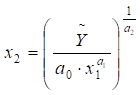(5.22)

Гранична норма заміни i-ого ресурсу j-им ресурсом:

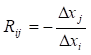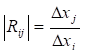; . (5.23)

Гранична норма заміни ресурсів Rij показує, на скільки одиниць збільшились затрати j-ого ресурсу (при незмінному випуску продукції), якщо затрати і-ого ресурсу зменшаться на одну одиницю.

Для двохфакторної виробничої функції Кобба-Дугласа:

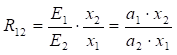. (5.24)

Еластичність заміщення ресурсів має вигляд :

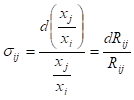. (5.25)

Еластичність заміщення ресурсів показує, на скільки відсотків повинно змінитись відношення ресурсів (при фіксованому випуску продукції), щоб гранична норма заміщення Rij змінилася на 1%.

6.   Геометрична інтерпретація основних характеристик виробничої функції Кобба-Дугласа.

1)  Ізокванта.

Виробничу функцію Кобба-Дугласа геометрично можна зобразити як поверхню в тримірному просторі з координатами Х₁, Х₂, У.

Для даної регресії геометричне місце точок з координатами (Х₁; Х₂), для яких показник виробництва обсягу продукції У є сталим (У=У₀=const), називається ізоквантою.

Запишемо рівняння ізокванти для фіксованого значення обсягу виробництва (У=У₀=const), для чого виразимо х₁ з формули (5.8):

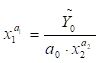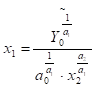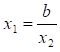; ; (якщо a₁=a₂). (5.26)

Відповідно до формули (5.26), ізокванта є спадною функцією (рис. 5.1).

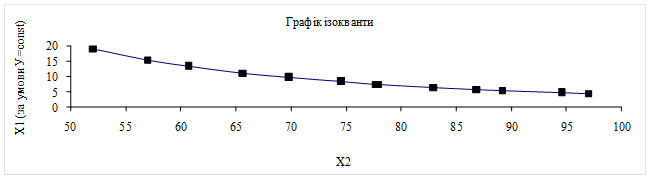
Рис. 5.1 – Графік ізокванти

2)  Виробнича функція Кобба-Дугласа при сталих затратах капіталу.

Розглянемо виробничу функцію Кобба-Дугласа при сталих затратах капіталу (х₂=х_{2 0}=const) і отримаємо:

. (5.27)

Відповідно до формули (5.27), виробничу функцію Кобба-Дугласа при сталих затратах капіталу є зростаючою функцією (рис. 5.2).

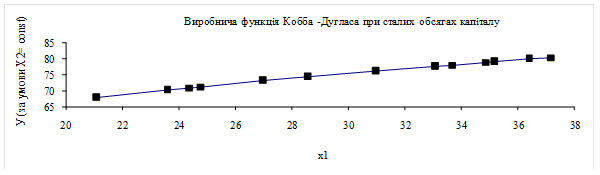
Рис. 5.2 – Виробнича функція Кобба-Дугласа при сталих затратах капіталу

3)  Виробнича функція Кобба-Дугласа при сталих затратах праці.

Розглянемо виробничу функцію Кобба-Дугласа при сталих затратах праці (х₁=х_{1 0}=const) і отримаємо:

. (5.28)

Відповідно до формули (5.28), виробничу функцію Кобба-Дугласа при сталих затратах праці є зростаючою функцією (рис. 5.3).

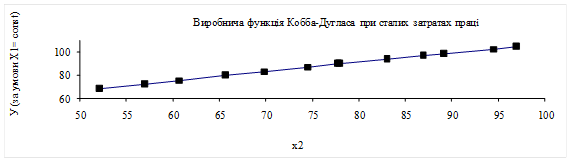
Рис. 5.3 – Виробнича функція Кобба-Дугласа при сталих затратах праці

4)  Гранична продуктивність праці при сталих обсягах капіталу.

Визначимо граничну продуктивність праці при сталих затратах капіталу (х₂=х_{2 0}=const):

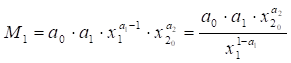. (5.29)

Відповідно до формули (5.29), гранична продуктивність праці при сталих затратах капіталу є спадною функцією (рис. 5.4).

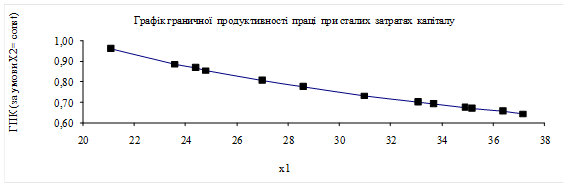
Рис. 5.4 – Графік граничної продуктивності праці при сталих затратах капіталу

5)  Гранична продуктивність капіталу при сталих обсягах праці.

Визначимо граничну продуктивність капіталу при сталих затратах праці (х₁=х_{1 0}=const):

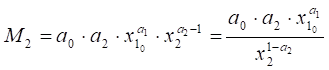. (5.30)

Відповідно до формули (5.29), гранична продуктивність капіталу при сталих затратах праці є спадною функцією (рис. 5.5).

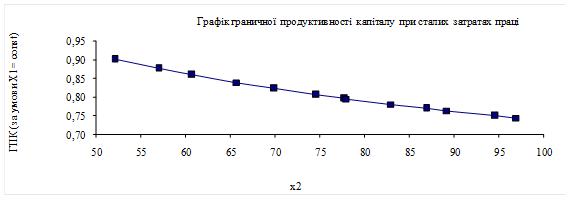
Рис. 5.4 – Графік граничної продуктивності капіталу при сталих затратах праці

Рекомендована література: [3; 6; 7; 8; 9].