Тема. Кореляційно-регресійний аналіз в
дослідженні соціально-економічних систем.
Мета:
Закріплення теоретичного матеріалу за темою «Статистичні методи перевірки гіпотез. Моделі кореляційно-регресійного аналізу розвитку соціально-економічних
систем». Набуття практичних навичок економетричного моделювання з використанням можливостей
табличного процесора MS Excel.
Завдання:
1.
Сформулювати гіпотезу про існування зв’язку між економічними величинами,
вибрати фактор (фактори) і показник.
2.
На основі статистичних даних побудувати
економетричні моделі для визначення впливу фактора
(факторів) на досліджуваний показник:
- на
мікрорівні – застосувати метод парної кореляції;
- на
макрорівні – застосувати метод множинної кореляції.
3.
Побудовані економетричні моделі перевірити на адекватність статистичним даним.
4. Провести
аналіз побудованих економетричних моделей.
5.
Розрахувати прогнозне значення показника та його довірчий інтвервал.
6. Зробити висновки.
Хід роботи.
Частина 1. Однофакторний кореляційний аналіз.
1)
Вибрати економічні показники діяльності і визначити, який з
них є фактором або незалежною змінною (Х),
а який результативним показником або залежною змінною (У).
2)
На основі даних статистики вибрати необхідні для дослідження
значення обраних економічних показників за 6-12 років і сформувати в програмі MS Excel масив
статистичних даних.
3)
Побудувати графік статистичних даних (поле кореляції) у такій
послідовності: виділити діапазон даних, вибрати на панелі інструментів вкладку
«вставлення», вибрати тип діаграми («точкова»), зазначити параметри діаграми
(назви осей, легенда).
Отримати
точкову діаграму – поле кореляції (рис. 1).
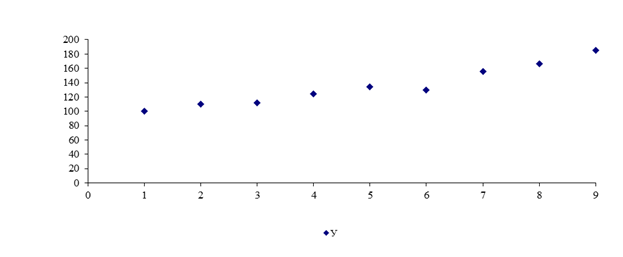
Рис. 1.
Поле кореляції
4)
Додати всі можливі лінії тренду (рис. 2, 3, 4, 5, 6).
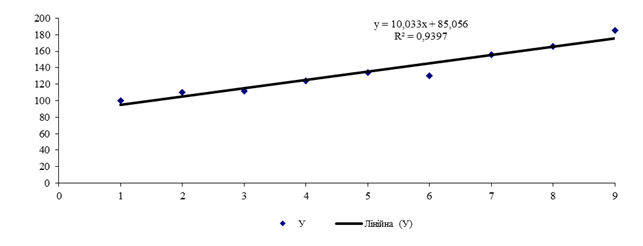
Рис. 2.
Поле кореляції та лінія тренду «лінійна»
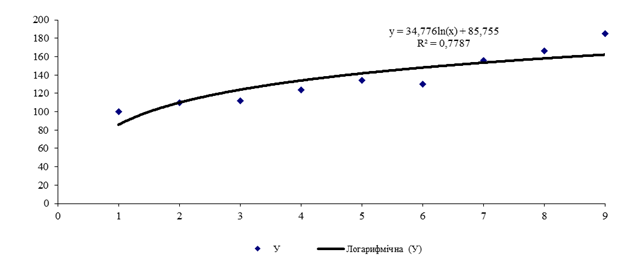
Рис. 3.
Поле кореляції та лінія тренду «логарифмічна»
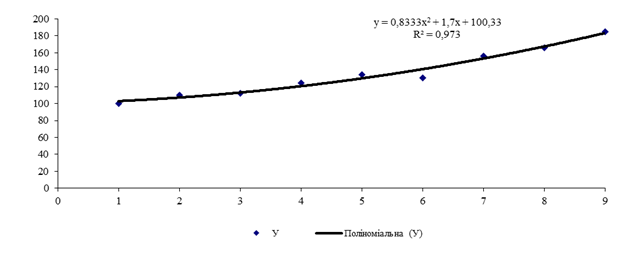
Рис. 4.
Поле кореляції та лінія тренду «поліноміальна» степеня 2
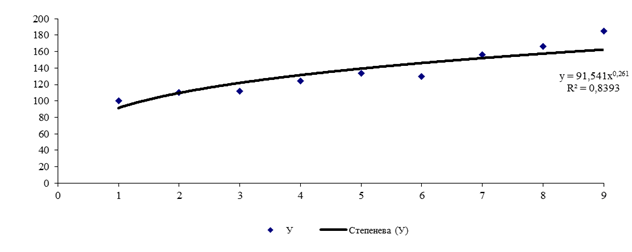
Рис. 5.
Поле кореляції та лінія тренду «степенева»
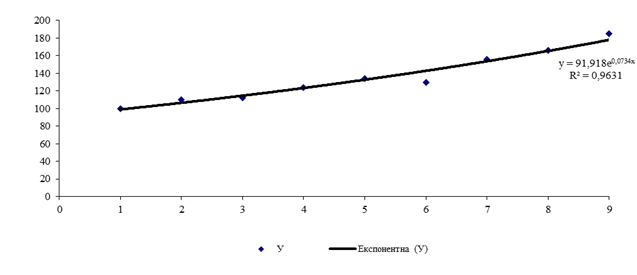
Рис. 6.
Поле кореляції та лінія тренду «експонентна»
ВАЖЛИВО. У
вкладці відкритого вікна «параметри» поставити позначки біля команд «показувати
рівняння на діаграмі» і «помістити на діаграму величину достовірності
апроксімації (R2)».
5)
Визначити аналітичну залежність, яка «найкраще» описує
статистичні дані. Критерієм вибору форми залежності (виду функції) вибрати
значення величини достовірності апроксімації R2. Чим ближче значення цього показника наближається до
одиниці, тим краще задана функція описує статистичні дані. Як видно, найбільш
оптимальна форма залежності подана на рис. 4, оскільки величини достовірності
апроксімації R2=0,973 є
найбільшою із розглянутих варіантів залежностей. Тому в розглянутому прикладі
будувати залежність між фактором і показником варто саме у вигляді полінома
другого степеня.
6)
Оцінити ступінь варіації показника У під впливом фактора Х
на основі значення коефіцієнт детермінації.
Кроки 7, 8,
9 виконувати лише для випадку лінійної залежності.
7)
Дати характеристику тісноти та напрямку зв’язку між фактором
і показником на основі значення коефіцієнта кореляції. Для цього розрахувати
коефіцієнт кореляції як квадратний корінь із коефіцієнта детермінації, оскільки
для парної лінійної регресії коефіцієнт детермінації дорівнює квадрату
коефіцієнта кореляції.
8)
Перевірити гіпотезу про значущість коефіцієнта кореляції,
розрахувавши значення статистики Стьюдента. Для цього розрахункове значення
статистики Стьюдента порівняти з табличним. Якщо ǀtрозǀ>ǀtpkǀ,
то із заданою надійністю відкинути гіпотезу про відсутність зв’язку між Х та У
і прийняти альтернативну їй гіпотезу про наявність залежності між випадковими величинами
фактора і показника.
9)
Провести аналіз якості існуючої залежності між величинами
фактора і показника, розрахувавши індекс кореляції як квадратний корінь із
коефіцієнта детермінації. Розрахувати надійні межі індексу кореляції і записати
надійний інтервал індексу кореляції.
10) Перевірити
побудовану модель на адекватність експериментальним даним за критерієм Фішера.
Для цього розрахункове значення критерію Фішера порівняти з табличним. Якщо Fроз>Fтабл, то побудовану економетричну модель вважати
адекватною експериментальним даним і придатною для подальшого аналізу та
прогнозування.
11) Розрахувати
прогнозне значення показника, підставивши прогнозне значення фактора у рівняння
регресії.
12) Розрахувати
коефіцієнт еластичності показника за фактором для заданих значень фактора і
прогнозного значення фактора.
13) На основі
проведених розрахунків побудувати графік коефіцієнта еластичності (рис. 7).
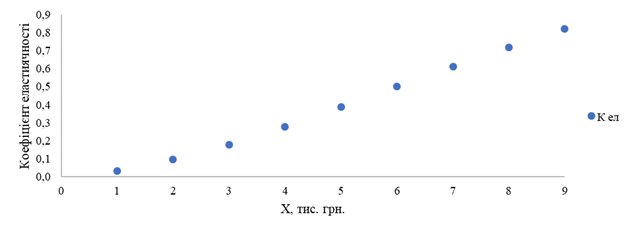
Рис. 7.
Графік коефіцієнта еластичності показника за фактором
Частина 2. Багатофакторний кореляційний аналіз.
1)
Вибрати економічні показники діяльності економіки країни або
галузі і визначити, які з них є факторами або незалежними змінними (Х1, Х2, і т.д.), а який є результативним показником або
залежною змінною (У).
2)
З даних Державної служби статистики України або обласних
управлінь статистики, інших джерел вибрати необхідні для дослідження значення
обраних економічних показників за 10-20 років і сформувати в програмі MS Excel масив статистичних даних (рис.
8).
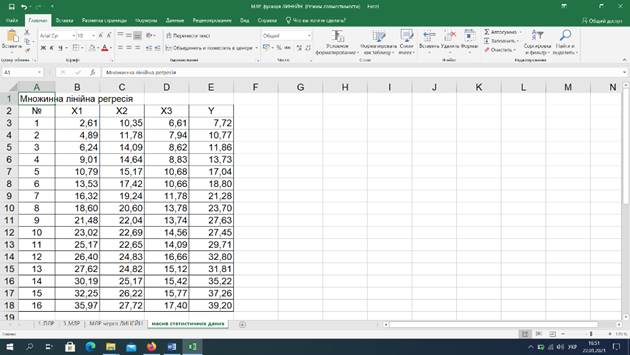
Рис. 8.
Масив статистичних даних для економетричного аналізу
3)
Використовуючи вбудовану функцію LINEST (ЛИНЕЙН) програми електронних таблиць MS Excel, отримати
параметри множинної лінійної регресії та статистичні характеристики отриманих
результатів (рис. 9).
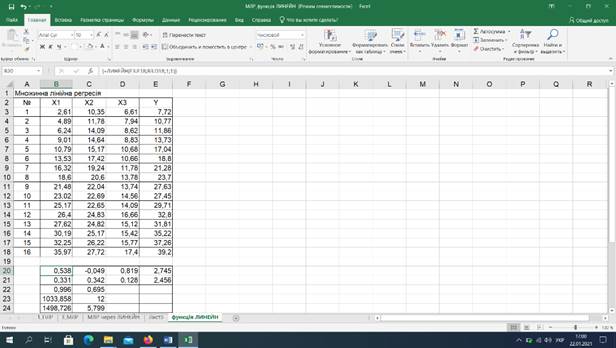
Рис. 9.
Результати застосування функції LINEST (ЛИНЕЙН)
4)
Записати отриману формулу множинної лінійної регресії та
пояснити зміст її коефіцієнтів.
5)
Обчислити розрахункові значення показника і переконатись, що
вони є близькими до відповідних статистичних значень показника (рис. 10).
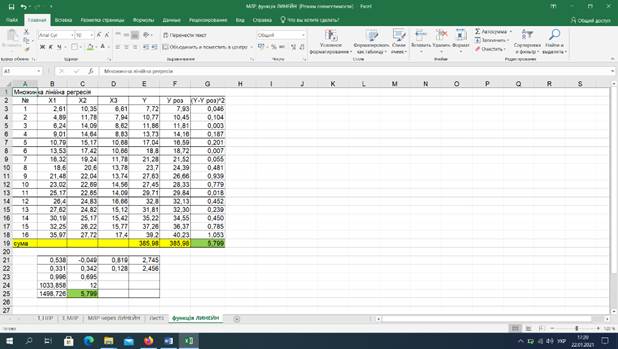
Рис. 10.
Порівняння статистичних і розрахункових значень показника
6)
Перевірити побудовану модель на адекватність
експериментальним даним за критерієм Фішера. Для цього отримане розрахункове
значення критерію Фішера порівняти з табличним. Якщо Fроз>Fтабл,
то побудовану економетричну модель вважати адекватною експериментальним даним і
придатною для подальшого аналізу та прогнозування.
7)
Оцінити ступінь варіації показника У під впливом факторів на основі значення коефіцієнт детермінації.
8)
Розрахувати прогнозне значення показника, підставивши
прогнозне значення фактора у рівняння регресії.
Література: [3; 7; 8; 11; 15; 26; 27; 29; 33].