Тема. Модель міжгалузевого балансу народного господарства.
Мета:
Закріплення теоретичного матеріалу за темою «Балансові моделі в економіці».
Набуття практичних навичок побудови та дослідження міжгалузевого балансу народного
господарства.
Завдання:
1. Скласти
міжгалузевий баланс народного господарства для трьох галузей виробництва і
споживання.
2.
Перевірити виконання основних балансових співвідношень.
2. Зробити висновки про
спрямованість кожної галузі щодо виробництва продукції – на кінцевих споживачів
чи на забезпечення діяльності інших галузей.
Хід роботи.
1)
Ознайомитись із теоретичними відомостями про матричні моделі загалом
і, зокрема, міжгалузевий баланс народного господарства.
2)
Вибрати варіант з додатка 1, який відповідає порядковому
номеру здобувача в списку групи (далі приклад з конкретними даними):
Вихідні дані до лабораторної роботи №1
|
Матриця коефіцієнтів прямих матеріальних затрат |
Кінцева продукція галузей |
Частка заробітної плати в чистій продукції |
Загальна рентабельність, % |
Питома вага ОВФ, % |
|||
|
0,30 |
0,25 |
0,20 |
56 |
0,42 |
18 |
80 |
|
|
0,15 |
0,12 |
0,03 |
20 |
0,71 |
14 |
44 |
|
|
0,10 |
0,05 |
0,08 |
12 |
0,36 |
22 |
52 |
|
3)
Скласти
основну систему рівнянь МГБ:
Х1 = 0,30 Х1 + 0,25 Х2
+ 0,20 Х3 + 56,
Х2 = 0,15 Х1 + 0,12 Х2
+ 0,03 Х3 + 20, (1)
Х3 = 0,10 Х1 + 0,05 Х2 +
0,08 Х3 + 12.
4)
Перенести
в ліву частину всі складові, які містять невідомі величини:
0,70 Х1 - 0,25 Х2 -
0,20 Х3 = 56,
-0,15 Х1+ 0,88 Х2 -
0,03 Х3 = 20, (2)
-0,10 Х1 - 0,05 Х2+ 0,92 Х3
= 12.
5) Розв’язати
систему лінійних рінянь (2) двома методами: методом оберненої матриці і методом
Крамера.
5.1. Метод
оберненої матриці
Скласти матрицю А з коефіцієнтів при змінних Х1, Х2, Х3 у лівій частині системи рівнянь (2) і вектор-стовпчик В з правих
частин рівнянь цієї системи:
А =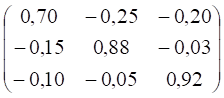
В =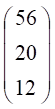
Побудувати матрицю А-1, обернену до матриці А,
використовуючи вбудовану функцію МОБР (MINVERSE) категорії «математичні»
програми MS Excel:
А-1 =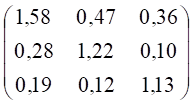
Виконати множення отриманої матриці А-1 на вектор В,
використовуючи вбудовану функцію МУМНОЖ (MMULT) категорії «математичні»
програми MS Excel:
А-1*В =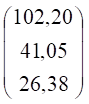
Отримані значення відповідають шуканим обсягам валової продукції
трьох галузей: Х1 = 102,20; Х2 = 41,05; Х3 = 26,38.
5.2. Метод Крамера
Використовуючи вбудовану функцію МОПРЕД (MDETERM) категорії «математичні»
програми MS Excel, розрахувати визначник системи (2):
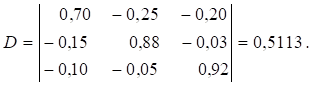
Обчислити визначники 
, які отримуємо
з 
заміною
j-го стовпчика на стовпчик
вільних членів Уі:
;
;
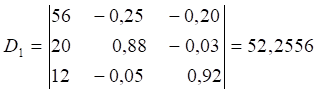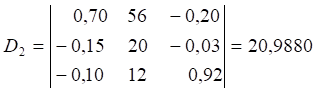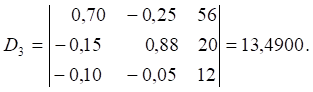
Розв’язок системи рівнянь (2) виражається формулами Крамера:
;
;
.
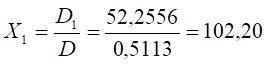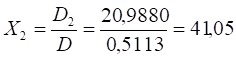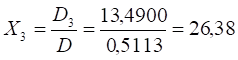Переконатись, що отримані результати співпадають із знайденими вище.
6)
Сформувати таблицю МГБ для трьох галузей народного
господарства (таблиця 1).
Таблиця 1
Міжгалузевий баланс народного господарства (загальна схема)
|
|
Сукупний суспільний продукт |
ВАЛОВА ПРОДУКЦІЯ |
|||||
|
|
Поточні виробничі потреби |
Кінцева продукція |
|||||
|
Галузі-виробники |
1 |
2 |
3 |
||||
|
Сукупний суспільний продукт |
Поточні матеріальні затрати |
1 |
X11 |
X12 |
X13 |
Y1 |
Х1 |
|
2 |
X21 |
X22 |
X23 |
Y2 |
Х2 |
||
|
3 |
X31 |
X32 |
X33 |
Y3 |
Х3 |
||
|
Чиста продукція |
Оплата праці |
V1 |
V2 |
V3 |
V+m |
- |
|
|
Чистий прибуток |
m1 |
m2 |
m3 |
- |
|||
|
ВАЛОВА ПРОДУКЦІЯ |
Х1 |
Х2 |
Х3 |
- |
|
||
7) Заповнити
другий квадрант таблиці МГБ даними в умові задачі значеннями кінцевої продукції
галузей: У1 = 56; У2 = 20; У3 = 12.
8) Заповнити останній
стовпчик і останній рядок таблиці МГБ розрахованими значеннями валової
продукції галузей: Х1 = 102,20; Х2 = 41,05; Х3 =
26,38.
9) Розрахувати
елементи другого квадранта (проміжну продукцію галузей або міжгалузеві потоки)
за формулою:
, (5)
де aij – коефіцієнти прямих
матеріальних затрат, які характеризують витрати продукції і-ої галузі на одиницю продукції j-ої
галузі. Ці коефіцієнти утворюють квадратну матрицю а=(аij) розмірності пхп і в задачі
відомі.
;
;
.
;
;
.
;
;
.
10)
Розрахувати чисту продукцію галузей за формулою:
.
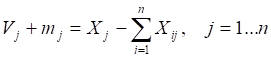(6)
V1+m1 = X1 - (X11+X21+X31) = 102,20 - (30,66+15,33+10,22) = 45,99;
V2+m2 = X2 - (X12+X22+X32) = 41,05 - (10,26+4,93+2,05) = 23,81;
V3+m3 = X3 - (X13+X23+X33) = 26,38 - (5,28+0,79+2,11) = 18,20.
11)
Знаючи частку заробітної плати в чистій продукції, визначити
заробітну плату для кожної галузі:
V1 = 0,42 ∙ (V1+m1) = 0,42 ∙ 45,99 = 19,32;
V2 = 0,42 ∙ (V2+m2) = 0,71 ∙ 23,81 = 16,91;
V3 = 0,42 ∙ (V3+m3) = 0,36 ∙ 18,20 = 6,55.
12)
Визначити чистий прибуток як різницю між чистою продукцією і
заробітною платою:
m1 = (V1+m1) - V1 = 45,99 - 19,32 = 26,67;
m2 = (V2+m2) - V2 = 23,81 - 16,91 = 6,9;
m3 = (V3+m3) - V3 = 18,20 - 6,55 = 11,65.
13)
Заповнити третій квадрант таблиці МГБ знайденими значеннями
заробітної плати і чистого прибутку.
14)
Розрахувати національний дохід (четвертий квадрант) як суму
елементів третього квадранта:
V+m = (V1+m1) + (V2+m2) + (V3+m3) = 45,99+28,81+18,20 = 88.
15)
Розрахувати суму валової продукції всіх галузей і записати її
в праву нижню комірку таблиці МГБ:
=
= 102,20 + 41,05 + 26,38 = 169,63.
16)
Заповнити всю матрицю МГБ:
Міжгалузевий баланс народного господарства
|
Галузі-споживачі |
Сукупний суспільний продукт |
ВАЛОВА ПРОДУКЦІЯ |
|||||
|
|
Поточні виробничі потреби |
Кінцева продукція |
|||||
|
Галузі-виробники |
1 |
2 |
3 |
||||
|
Сукупний суспільний продукт |
Поточні матеріальні затрати |
1 |
30,66 |
10,26 |
5,28 |
56 |
102,20 |
|
2 |
15,33 |
4,93 |
0,79 |
20 |
41,05 |
||
|
3 |
10,22 |
2,05 |
2,11 |
12 |
26,38 |
||
|
Чиста продукція |
Оплата праці |
19,32 |
16,91 |
6,55 |
88 |
- |
|
|
Чистий прибуток |
26,67 |
6,9 |
11,65 |
- |
|||
|
ВАЛОВА ПРОДУКЦІЯ |
102,20 |
41,05 |
26,38 |
- |
169,63 |
||
17)
Переконатись, чи виконується рівність чистої і кінцевої
продукції для всіх галузей наодного господарства:
У1
+ У2 + У3 = 56 + 20 + 12 = 88.
18)
Визначити, до якої галузі (умовно – важкої чи легкої
промисловості) можна віднести три досліджувані галузі народного господарства,
порівнявши для кожної з них чисту і кінцеву продукцію:
Порівняння чистої і кінцевої продукції галузей
|
Галузь |
Кінцева продукція (КП) |
Чиста продукція (ЧП) |
Умова |
Висновок |
|
1 |
56 |
45,99 |
КП>ЧП |
Легка промисловість |
|
2 |
20 |
23,81 |
КП<ЧП |
Важка промисловість |
|
3 |
12 |
18,20 |
КП<ЧП |
Важка промисловість |
Література: [3; 7; 8; 11; 15; 27].
Додаток 1
Дані для виконання лабораторної роботи №1
|
№ з/п |
Матриця коефіцієнтів прямих матеріальних затрат |
Кінцева продукція галузей |
Частка з/п в чистій продукції |
|||
|
1 |
0,41 |
0,32 |
0,25 |
80 |
0,42 |
|
|
0,18 |
0,20 |
0,10 |
30 |
0,71 |
||
|
0,15 |
0,11 |
0,13 |
25 |
0,36 |
||
|
2 |
0,35 |
0,29 |
0,21 |
200 |
0,48 |
|
|
0,20 |
0,16 |
0,12 |
80 |
0,63 |
||
|
0,12 |
0,08 |
0,15 |
55 |
0,37 |
||
|
3 |
0,32 |
0,22 |
0,18 |
150 |
0,38 |
|
|
0,14 |
0,20 |
0,08 |
60 |
0,65 |
||
|
0,10 |
0,08 |
0,12 |
40 |
0,32 |
||
|
4 |
0,28 |
0,22 |
0,16 |
500 |
0,44 |
|
|
0,14 |
0,16 |
0,06 |
200 |
0,68 |
||
|
0,12 |
0,07 |
0,10 |
150 |
0,27 |
||
|
5 |
0,36 |
0,30 |
0,25 |
100 |
0,40 |
|
|
0,17 |
0,15 |
0,07 |
40 |
0,74 |
||
|
0,13 |
0,09 |
0,11 |
28 |
0,32 |
||
|
6 |
0,32 |
0,25 |
0,21 |
360 |
0,36 |
|
|
0,20 |
0,15 |
0,10 |
150 |
0,60 |
||
|
0,17 |
0,11 |
0,14 |
110 |
0,25 |
||
|
7 |
0,41 |
0,32 |
0,25 |
200 |
0,38 |
|
|
0,18 |
0,20 |
0,10 |
80 |
0,65 |
||
|
0,15 |
0,11 |
0,13 |
55 |
0,32 |
||
|
8 |
0,35 |
0,29 |
0,21 |
150 |
0,44 |
|
|
0,20 |
0,16 |
0,12 |
60 |
0,68 |
||
|
0,12 |
0,08 |
0,15 |
40 |
0,27 |
||
|
9 |
0,32 |
0,22 |
0,18 |
500 |
0,40 |
|
|
0,14 |
0,20 |
0,08 |
200 |
0,74 |
||
|
0,10 |
0,08 |
0,12 |
150 |
0,32 |
||
|
10 |
0,28 |
0,22 |
0,16 |
100 |
0,36 |
|
|
0,14 |
0,16 |
0,06 |
40 |
0,60 |
||
|
0,12 |
0,07 |
0,10 |
28 |
0,25 |
||
