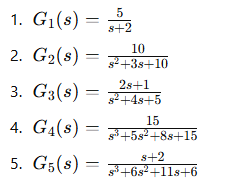Лабораторна робота 14

Тема. Вивчення методів підвищення точності регулювання в сталих режимах

Мета роботи: Ознайомлення з методами підвищення точності регулювання в сталих режимах роботи систем автоматичного керування (САК), дослідження впливу різних підходів на покращення якості регулювання.

Точність регулювання визначається відхиленням вихідної величини від заданого значення у сталому режимі. Основними методами підвищення точності регулювання є:

1.      Застосування регуляторів з інтегральною складовою

o    ПІ, ПІД-регулятори дозволяють зменшити статичну похибку завдяки інтегральному ефекту.

2.      Збільшення коефіцієнта підсилення системи

o    Підвищення підсилення зменшує похибку, але може знизити стійкість системи.

3.      Застосування зворотного зв'язку

o    Використання негативного зворотного зв'язку покращує точність та стабільність роботи системи.

4.      Використання компенсаційних пристроїв

o    Введення додаткових коригуючих ланок дозволяє покращити характеристики системи.

5.      Адаптивне регулювання

o    Автоматичне налаштування параметрів регулятора для оптимальної роботи при змінних умовах.

Приклад: Розглянемо лінійну систему другого порядку, що описується рівнянням:

1.      Для цієї системи проведемо дослідження в MATLAB без покращення та з використанням ПІ та ПІД регуляторів з передавальною функцією:

(ПІ)

+(ПІД)

та оцінимо їх вплив на точність

2.      Побудуємо її перехідний процес у MATLAB та визначимо статичну похибку

3.      Змінюємо коефіцієнт підсилення K та аналізуємо ефект на вихідну похибку та стійкість.

4.      Впроваджуємо негативний зворотний зв'язок та оцінюємо покращення стабільності.

5.      Використаємо адаптивне регулювання та порівняємо отримані результати.

Побудова графіків для аналізу поведінки системи використаємо MATLAB. Відкриємо MATLAB і виконаємо наступний код, лістинг 1.

Лістинг 1 – Код програми

s = tf('s');

G = 10 / (s^2 + 3*s + 10);

figure;

step(G);

grid on;

title('Перехідний процес без регулятора');

% ПІ-регулятор

Kp = 2;

Ki = 5;

PI_controller = Kp + Ki/s;

G_PI = feedback(G * PI_controller, 1)

% ПІД-регулятор

Kd = 1;

PID_controller = Kp + Ki/s + Kd*s;

G_PID = feedback(G * PID_controller, 1);

% Аналіз стійкості

figure;

rlocus(G_PID);

title('Корені характеристичного рівняння (Root Locus)');

grid on;

figure;

margin(G_PID);

title('Діаграма Боде для аналізу запасу стійкості');

grid on;

figure;

nyquist(G_PID);

title('Годограф Найквіста');

grid on;

figure;

hold on;

step(G, 'k');

step(G_PI, 'b');

step(G_PID, 'r');

grid on;

xlabel('Час, с');

ylabel('Вихідна величина');

title('Порівняння регулювання: без регулятора, ПІ та ПІД');

legend('Без регулятора', 'ПІ-регулятор', 'ПІД-регулятор');

hold off;

Кінець лістингу 1

Під проведених розрахунків та моделювання з використання Matlab, отримуємо наступні характеристики, що подані в таблиці 1

Таблиця 1 – Результати дослідження

Назва характеристики	Графічне відображення
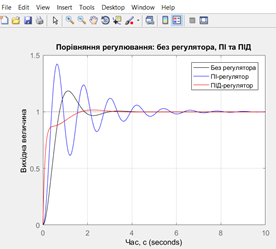
Перехідні характеристики без регулятора та з ПІ і ПІД
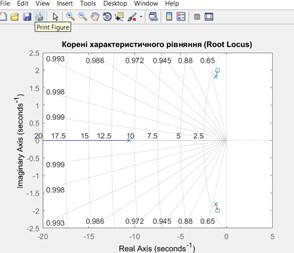
Розміщення коренів на комплексній площині
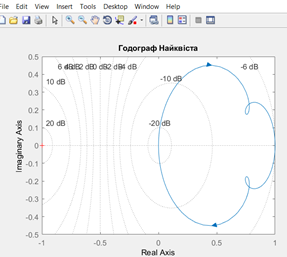
Характеристика за критерієм Найквіста
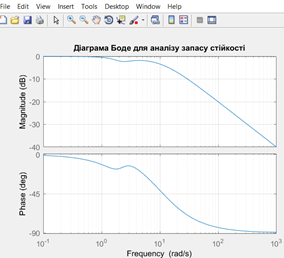
Діаграма Боде

За результатами проведених досліджень можна зробити наступні висновки, щодо точності та стійкості системи:

1.     Додавання ПІ-регулятора дозволило значно зменшити статичну похибку, оскільки інтегральна складова компенсувала стале відхилення. Подальше впровадження ПІД-регулятора додатково покращило динамічні характеристики системи, зменшуючи перерегулювання та скорочуючи час перехідного процесу.

2.     Аналіз зміни коефіцієнта підсилення показав, що його збільшення дозволяє зменшити похибку, але водночас може призвести до втрати стійкості. Впровадження негативного зворотного зв’язку дозволило покращити стабільність системи та зменшити вплив збурень.

3.     Дослідження запасу стійкості за допомогою кореневого годографа, діаграми Боде та годографа Найквіста підтвердило, що використання ПІД-регулятора з правильно підібраними параметрами значно покращує як точність регулювання, так і стабільність системи.

Таким чином, комбіноване використання ПІД-регулятора та зворотного зв’язку є ефективним методом покращення точності регулювання, зменшення статичної похибки та забезпечення стійкості системи.

Завдання для виконання

Проведіть дослідження систем керування, передаточні функції яких подані в таблиці 2. Коефіцієнти передаточних змінити згідно порядкового номера академічної групи, н-д а0 та k+№(порядковий номер)

Таблиця 1 – Варіанти завдань

	1	Визначте статичну похибку регулювання для одиничного східчастого входу для кожної передаточної функції.
	2	Побудуйте перехідну характеристику кожної системи та визначте основні параметри: 1.     Час встановлення 2.     Перерегулювання 3.     Статичну похибку
	3	Додайте П-регулятор (пропорційне регулювання) та оцініть зміни у точності регулювання.
	4	Додайте інтегральну складову (ПІ-регулятор) та проаналізуйте, як вона впливає на статичну похибку та якість регулювання
	5	Впровадьте ПІД-регулятор та оцініть його вплив на швидкодію та точність регулювання.
	6	Для кожної передаточної функції змініть коефіцієнт підсилення від 1 до 20 та оцініть, як це впливає на статичну похибку.

Додаткове завдання:

1. Побудуйте годограф Найквіста для кожної системи та визначте, чи є вона стійкою.

2. Побудуйте діаграми Боде та оцініть запас стійкості.

3. Використайте кореневий годограф, щоб дослідити, як змінюється стійкість при збільшенні коефіцієнта підсилення.