ЛЕКЦІЯ 7. «Автокореляція
залишків»
Анотація
Поняття автокореляції. Автокореляція залишків. Лагові затримки.
Природа автокореляції та її наслідки. Методи усунення автокореляції. Тестування наявності
автокореляції. Критерій Дарбіна-Уотсона. Критерій фон
Неймана. Коефіцієнти автокореляції та їх
застосування. Автокореляційна функція та корелограма. Оцінка параметрів моделі з автокорельованими
залишками. Метод Ейткена. Метод Кочрена-Оркатта.
Прогноз на основі моделі з автокорельованими
залишками.
7.1 Природа автокореляції та її наслідки
Автокореляція – це взаємозв’язок
послідовних елементів часового чи просторового ряду даних.
В економетричних
дослідженнях часто зустрічаються такі випадки, коли дисперсія залишків є постійною,
але спостерігається їх коваріація. Це явище має назву
автокореляції залишків. В економетричних моделях автокореляція залишків має особливе
значення, оскільки при її наявності порушується одна з умов, що висуваються при оцінці параметрів моделі за методом 1МНК.
Автокореляція залишків виникає найчастіше тоді, коли економетрична модель будується на основі часових рядів.
Якщо існує кореляція між послідовними значеннями деякої незалежної змінної, то спостерігатиметься й кореляція послідовних значень залишків,
так звані лагові затримки
(запізнювання) в економічних процесах.
Тобто в цьому випадку також
порушується гіпотеза, згідно з якою ![]() але при гетероскедастичності змінюється дисперсія залишків при
відсутності їх коваріації, а при автокореляції –
існує коваріація залишків при незмінній дисперсії.
але при гетероскедастичності змінюється дисперсія залишків при
відсутності їх коваріації, а при автокореляції –
існує коваріація залишків при незмінній дисперсії.
При автокореляції залишків,
як і при гетероскедастичності дисперсія залишків
запишеться:
![]() (7.1)
(7.1)
але матриця ![]() матиме тут зовсім
інший вигляд. Запишемо цю матрицю:
матиме тут зовсім
інший вигляд. Запишемо цю матрицю:
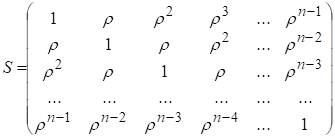 . (7.2)
. (7.2)
В даній матриці параметр r характеризує коваріацію кожного
наступного значення залишків із попереднім. Так, якщо для залишків записати авторегресійну модель першого порядку:
![]() , (7.3)
, (7.3)
то r характеризує силу зв’язку величини залишків у період t від величини залишків у період t – 1.
Якщо проігнорувати матрицю ![]() при визначенні
дисперсії залишків, і для оцінки параметрів моделі застосувати метод 1МНК, то можливі
такі наслідки:
при визначенні
дисперсії залишків, і для оцінки параметрів моделі застосувати метод 1МНК, то можливі
такі наслідки:
1) оцінки параметрів моделі можуть бути незміщеними, але
неефективними, тобто вибіркові дисперсії вектора
оцінок ![]() можуть бути
невиправдано великими;
можуть бути
невиправдано великими;
2) статистичні критерії t
і F- статистики, які отримані для класичної
лінійної моделі, практично не можуть бути використані для дисперсійного
аналізу, бо їх розрахунок не враховує наявності коваріації
залишків;
3) неефективність оцінок параметрів економетричної
моделі, як правило, призводить до неефективних прогнозів, тобто прогнозні
значення матимуть велику вибіркову дисперсію.
Автокореляція може виникати через інерційність і циклічність
багатьох економічних процесів. Провокувати автокореляцію також може неправильно
специфікована функціональна залежність у регресійних моделях. Наприклад, модель
може не включати істотній фактор, яким часто виступає фактор часу.
При чому важливо відрізняти від істинної автокореляції залишків
випадки неправильної специфікації моделі. Оскільки в останньому випадку
необхідно змінити форму моделі. При цьому можуть використовуватися різні методи усунення автокореляції, наприклад:
-
введення у модель фактору часу;
-
перехід до темпових чи відносних показників;
-
включення у модель неврахованих факторів;
-
побудова авто регресійних рівнянь.
У випадку ж істинної
автокореляції залишків застосовують спеціальні методи оцінки параметрів
регресії з автокорельованими залишками.
7.2 Методи визначення автокореляції
Тестування наявності
автокореляції, як правило, здійснюється за d-тестом
Дарбіна-Уотсона, хоча існують й інші не менш відомі
тести: критерій фон Неймана, нециклічний коефіцієнт
автокореляції, циклічний коефіцієнт автокореляції.
7.2.1 Критерій Дарбіна-Уотсона
Cкладається з кількох етапів і включає
зони невизначеності.
Крок 1. Розраховується
значення d-статистики за формулою
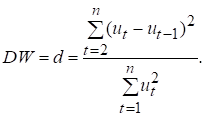 (7.4)
(7.4)
Доведено, що значення d-статистики Дарбіна-Уотсона
перебуває в межах 0 < DW < 4.
Крок 2. Задаємо рівень
значущості a. За таблицею Дарбіна-Уотсона при заданому рівні значущості a, кількості факторів m і
кількості спостережень n знаходимо
два значення DW1 і DW2:
-
якщо 0< DW<DW1, то наявна додатна автокореляція;
-
якщо DW1 <DW< DW2 або 4-DW2<
DW < 4-DW1, то ми не можемо зробити висновки ані про наявність,
ані про відсутність автокореляції (DW потрапляє в зону невизначеності);
-
якщо 4-DW1 < DW < 4, маємо від’ємну
автокореляцію;
-
якщо DW2 < DW < 4-DW2, то
автокореляція відсутня.
Графічне зображення розподілу ілюструє
рис. 7.1.
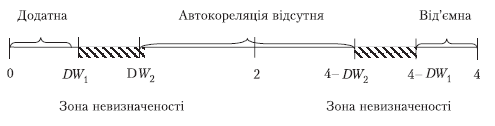
Рисунок 7.1 – Зони автокореляційного зв’язку за критерієм Дарбіна-Уотсона
Тест Дарбіна-Уотсона
можна застосовувати лише в тому випадку, якщо:
а) в регресійному
рівнянні присутній вільний член;
б) регрессори є нестохастичними;
в) в регресійному
рівнянні немає лагових значень залежної змінної.
7.2.2 Критерій фон Неймана
Для виявлення автокореляції
залишків використовується також критерій фон Неймана:
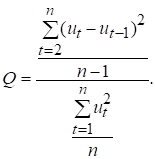 (7.5)
(7.5)
Звідси ![]() . При
. При ![]() . Фактичне значення критерію фон Неймана
порівнюється з табличним для вибраного рівня значущості і заданого числа
спостережень. Якщо
. Фактичне значення критерію фон Неймана
порівнюється з табличним для вибраного рівня значущості і заданого числа
спостережень. Якщо ![]() , то існує додатна автокореляція.
, то існує додатна автокореляція.
7.2.3 Коефіцієнти
автокореляції та їх застосування
Цей коефіцієнт виражає ступінь
взаємозв’язку залишків кожного наступного значення з попереднім, а саме:
I ряд – ![]() ;
;
II ряд – ![]() .
.
Він обчислюється за формулою:
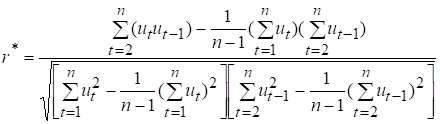 (7.6)
(7.6)
Коефіцієнт ![]() може набувати значень
в інтервалі (–1;+1). Від’ємні значення його свідчать про від’ємну
автокореляцію, додатні – про додатну. Значення, що містяться в деякій
критичній області біля нуля, свідчать про відсутність автокореляції, тобто стверджують
нульову гіпотезу про відсутність автокореляції залишків. Оскільки ймовірнісний
розподіл
може набувати значень
в інтервалі (–1;+1). Від’ємні значення його свідчать про від’ємну
автокореляцію, додатні – про додатну. Значення, що містяться в деякій
критичній області біля нуля, свідчать про відсутність автокореляції, тобто стверджують
нульову гіпотезу про відсутність автокореляції залишків. Оскільки ймовірнісний
розподіл ![]() встановити трудно, то
на практиці замість
встановити трудно, то
на практиці замість ![]() обчислюють циклічний
коефіцієнт автокореляції
обчислюють циклічний
коефіцієнт автокореляції ![]() .
.
Загалом, якщо часовий ряд має циклічний характер, тобто
припускається, що після значення ![]() загальний характер зміни членів ряду
повторюється, то автокореляцію визначають за допомогою коефіцієнта r0, запровадженого
Андерсоном.
загальний характер зміни членів ряду
повторюється, то автокореляцію визначають за допомогою коефіцієнта r0, запровадженого
Андерсоном.
У цьому разі автокореляція визначається між послідовностями,
зсунутими на період t:
![]()
Якщо період t=1, то маємо коефіцієнт циклічної автокореляції першого порядку,
який відбиває інтенсивність взаємозв’язку між послідовностями:
I ряд – ![]() ,
, ![]() ;
;
II ряд – ![]() ,
, ![]() .
.
Циклічний коефіцієнт
обчислюється за формулою:
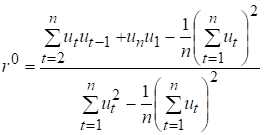 (7.7)
(7.7)
Для досить довгих рядів вплив
циклічних членів на величину коефіцієнта ![]() незначний, тому можна
вважати, що ймовірнісний розподіл
незначний, тому можна
вважати, що ймовірнісний розподіл ![]() наближається до
розподілу
наближається до
розподілу ![]() . Якщо останній член ряду дорівнює першому, тобто u1 = un, то нециклічний
коефіцієнт автокореляції дорівнює циклічному. Очевидно, що коли залишки не
містять тренду, то припущення про рівність u1 = un
недалеке від реальності і циклічний коефіцієнт автокореляції наближається до
нециклічного.
. Якщо останній член ряду дорівнює першому, тобто u1 = un, то нециклічний
коефіцієнт автокореляції дорівнює циклічному. Очевидно, що коли залишки не
містять тренду, то припущення про рівність u1 = un
недалеке від реальності і циклічний коефіцієнт автокореляції наближається до
нециклічного.
Фактично обчислене значення
циклічного коефіцієнта автокореляції порівнюється з табличним для вибраного
рівня значущості і довжини ряду n.
Якщо ![]() , то існує автокореляція. Припускаючи, що
, то існує автокореляція. Припускаючи, що 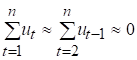 , циклічний коефіцієнт автокореляції можна записати у вигляді
, циклічний коефіцієнт автокореляції можна записати у вигляді
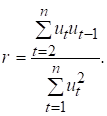 (7.8)
(7.8)
На практиці часто замість
(7.8) обчислюють
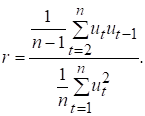 (7.9)
(7.9)
Аналогічно можна визначити
коефіцієнти другого та більш високого порядків (в формулах 7.6-7.9 замість ![]() використовують
використовують ![]() , а сумують починаючи не з 2, а з
, а сумують починаючи не з 2, а з ![]() ).
).
Число періодів, за якими
розраховується коефіцієнт автокореляції, називається лагом. Однак, зі збільшенням лагу число пар значень, по яким
розраховується коефіцієнт, зменшується. Вважається доцільним для забезпечення
статистичної достовірності коефіцієнтів використовувати правило, що
максимальний лаг не повинен перевищувати n/4.
Властивості коефіцієнта
автокореляції:
1) він характеризує тісноту лінійного зв’язку поточного та
попередніх рівнів ряду і при наявності сильного нелінійного зв’язку може
прямувати до 0;
2) по знаку коефіцієнта кореляції не можна робити висновок про
зростаючу чи спадну тенденцію в рівнях ряду; більшість часових рядів
економічних даних містять додатну автокореляцію рівнів, але при цьому можуть
мати спадну тенденцію.
Послідовність коефіцієнтів
автокореляції рівнів першого, другого та наступних порядків називають автокореляційною функцією часового ряду. Графік
залежності її значень від величини лагу називається корелограмою. За даними функцією
та графіком можна визначити структуру ряду.
Приклад.
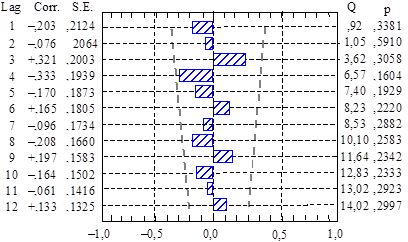
Рисунок
2 – Корелограма ряду залишків (побудовано в ПП Statistica)
На графіку точками позначено
дві симетричні прямі, які визначають 95 %-ві межі
значущості коефіцієнта автокореляції (± дві стандартні похибки, тобто ![]() = 0,417, де n = 24.
Точніше, n = 23 за k = 1 i n = 22 за k = 2 тощо).
Оскільки жоден із коефіцієнтів автокореляції не лежить за цими межами, а в зміні
значень коефіцієнтів відсутня певна закономірність, можна вважати, що в цьому
разі ряд залишків не містить систематичної складової.
= 0,417, де n = 24.
Точніше, n = 23 за k = 1 i n = 22 за k = 2 тощо).
Оскільки жоден із коефіцієнтів автокореляції не лежить за цими межами, а в зміні
значень коефіцієнтів відсутня певна закономірність, можна вважати, що в цьому
разі ряд залишків не містить систематичної складової.
7.3 Оцінка параметрів моделі з автокорельованими
залишками
Оцінку параметрів моделі з автокорельованими залишками можна виконувати на основі
чотирьох методів:
1) Ейткена;
2) перетворення вихідної інформації;
3) Кочрена-Оркатта;
4) Дарбіна.
Перші два методи доцільно
застосовувати тоді, коли залишки описуються авторегресійною
моделлю першого порядку (7.3).
Ітераційні методи Кочрена-Оркатта і Дарбіна можна
застосовувати для оцінки параметрів економетричної
моделі також і тоді, коли залишки описуються авторегресійною
моделлю вищого порядку:
![]() . (7.10)
. (7.10)
7.3.1 Метод Ейткена (УМНК)
Як зазначалося, оператор
оцінювання УМНК можна записати так:
![]() (7.11)
(7.11)
де ![]() – вектор оцінок параметрів економетричної
моделі;
– вектор оцінок параметрів економетричної
моделі;
![]()
![]() – матриця, обернена до матриці кореляції залишків;
– матриця, обернена до матриці кореляції залишків;
![]() – матриця, обернена до матриці V, де
– матриця, обернена до матриці V, де ![]() , а
, а ![]() – залишкова дисперсія.
– залишкова дисперсія.
Звідси
![]() (7.12)
(7.12)
Отже, щоб оцінити параметри
моделі на основі методу Ейткена, треба сформувати
матрицю S (7.2).
У цій симетричній матриці ![]() виражає коефіцієнт
автокореляції s-го порядку для
залишків
виражає коефіцієнт
автокореляції s-го порядку для
залишків ![]() . Очевидно, що коефіцієнт автокореляції нульового порядку дорівнює
1.
. Очевидно, що коефіцієнт автокореляції нульового порядку дорівнює
1.
Оскільки коваріація
залишків ![]() при s > 2
часто наближається до нуля, то матриця, обернена до матриці S, матиме такий вигляд:
при s > 2
часто наближається до нуля, то матриця, обернена до матриці S, матиме такий вигляд:
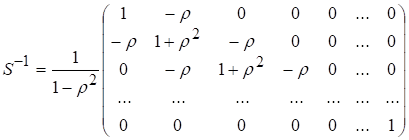 (7.13)
(7.13)
Таку матрицю іноді
пропонується використовувати при оцінюванні параметрів моделі з автокорельованими залишками за методом Ейткена.
При цьому для обчислення r
використовується циклічний коефіцієнт кореляції r, розрахований за формулою
(7.8) або (7.9).
Зауважимо, що параметр r (або ![]() ) має зміщення. Тому, використовуючи такий параметр для
формування матриці S, необхідно
скоригувати його на величину зміщення
) має зміщення. Тому, використовуючи такий параметр для
формування матриці S, необхідно
скоригувати його на величину зміщення
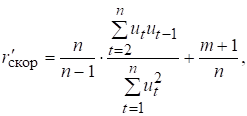 (7.14)
(7.14)
де ![]() – величина зміщення (m – кількість незалежних змінних).
– величина зміщення (m – кількість незалежних змінних).
7.3.2 Метод Кочрена-Оркатта
Нехай задано економетричну модель
![]() (7.15)
(7.15)
![]()
Перетворивши вихідну інформацію за допомогою ![]() , дістанемо:
, дістанемо:
![]() (7.16)
(7.16)
У цій моделі залишки ![]() мають
скалярну дисперсійну матрицю.
мають
скалярну дисперсійну матрицю.
Сума квадратів залишків
на основі (7.16) визначатиметься
співвідношенням
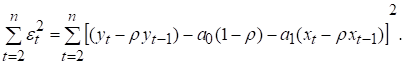 (7.17)
(7.17)
Безпосередня мінімізація функції (7.17) приводить до системи
нелінійних рівнянь, тому аналітичний вираз оцінок параметрів ![]() ,
, ![]() і
і ![]() дістати
важко.
дістати
важко.
Метод наближеного пошуку
параметрів ![]() ,
, ![]() і
і ![]() , які мінімізують
суму квадратів (7.17), дає ітеративний метод, запропонований
Кочреном і Оркаттом і
названий на їхню честь.
, які мінімізують
суму квадратів (7.17), дає ітеративний метод, запропонований
Кочреном і Оркаттом і
названий на їхню честь.
Опишемо його алгоритм.
Крок 1. Довільно вибирають значення параметра ![]() , наприклад
, наприклад ![]() Підставивши
його в (7.17), обчислюють
Підставивши
його в (7.17), обчислюють ![]() і
і ![]() .
.
Крок 2. Поклавши ![]() і
і ![]() , підставимо їх
у (7.17) і обчислимо
, підставимо їх
у (7.17) і обчислимо ![]()
Крок 3. Підставивши в співвідношення (7.17) значення ![]() , знайдемо
, знайдемо ![]() і
і ![]() .
.
Крок 4. Використаємо ![]() і
і ![]() для мінімізації суми квадратів залишків (7.17) за невідомим параметром
для мінімізації суми квадратів залишків (7.17) за невідомим параметром ![]() . Процедура триває доти, доки наступні значення параметрів
. Процедура триває доти, доки наступні значення параметрів ![]() ,
, ![]() і
і ![]() не будуть
відрізнятись менш як на задану величину.
не будуть
відрізнятись менш як на задану величину.
Проведені дослідження
показали, що в результаті застосування методу Кочрена-Оркатта
завжди знаходимо глобальний оптимум і алгоритм забезпечує
порівняно добру збіжність.
7.4 Прогноз результативного показника
Нехай маємо модель: ![]() де
де ![]() і
і ![]() яка побудована для n спостережень.
яка побудована для n спостережень.
Використаємо цю модель для визначення прогнозу залежної змінної ![]() для періоду n +1 коли для цього
періоду задано незалежну змінну
для періоду n +1 коли для цього
періоду задано незалежну змінну ![]() . Формула дає найкращий незміщений прогноз:
. Формула дає найкращий незміщений прогноз:
![]()
де ![]() – оцінка параметрів
моделі згідно з методом Ейткена,
– оцінка параметрів
моделі згідно з методом Ейткена,
![]() і
і 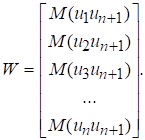
Якщо залишки описуються авторегресійною моделлю першого порядку, то з урахуванням рівності ![]() можна
записати:
можна
записати:
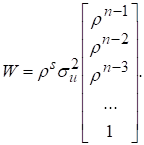
Отже, вектор W
можна дістати, помноживши ![]() на останній
стовпець матриці V. Але оскільки
на останній
стовпець матриці V. Але оскільки
![]() , то добуток
, то добуток ![]() являє
собою останній рядок матриці
E, помножений
на
являє
собою останній рядок матриці
E, помножений
на ![]() .
.
Звідси ![]() .
.
Формула прогнозу має вигляд
![]() (7.16)
(7.16)