ЛЕКЦІЯ 6. «Гетероскедастичність залишків»

Анотація

Поняття гомоскедастичності та гетероскедастичності залишків. Наслідки порушень припущення про гомоскедастичність. Методи виявлення гетероскедастичності. Тест Голдфельда-Квандта. Тест рангової кореляції Спірмена. Перевірка гетероскедастичності на основі критерію m. Тест Глейсера. Трансформування початкової моделі з гетероскедастичністю. Зважений метод найменших квадратів. Оцінювання параметрів регресії за допомогою узагальненого методу найменших квадратів (методу Ейткена).

6.1 Поняття гетероскедастичності

Передумови, які висуваються при оцінці параметрів моделі за методом 1МНК на практиці часто можуть порушуватись. Однією з таких передумов є незмінність дисперсії залишків для всіх спостережень вихідної сукупності (гомоскедастичність). В практичних дослідженнях вона часто порушується. Наприклад, в економетричній моделі, що характеризує залежність витрат на споживання від доходу, дисперcія залишків може змінюватись для спостережень, які відносяться до різних груп населення за розміром доходів.

Якщо дисперсія залишків в економетричному моделюванні змінюється для кожного спостереження або для груп спостережень, то це явище називається гетероскедастичністю.

Сутність припущення про гомоскедастичність полягає в тому, що варіація кожної випадкової складової навколо її математичного сподівання не залежить від значення факторів :

(6.1)

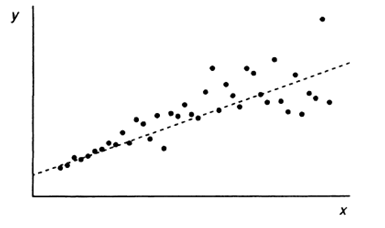
Рисунок 6.1 – Модель з гетероскедастичним випадковим членом

Форма гетероскедастичності залежить від знаків і значень пояснюючих факторів.

(6.2)

Оскільки  – не спостережувана випадкова величина, то ми не знаємо справжньої форми гетероскедастичності. У прикладних дослідженнях, як правило, використовують зручне припущення, а саме в разі простої лінійної регресії гетероскедастичність має форму

, (6.3)

(, яку необхідно оцінити).

Наслідки порушень припущення про гомоскедастичність:

1) неможливо знайти середньоквадратичне відхилення параметрів регресії, а отже, неможливо оцінити значущість параметрів;

2) неможливо побудувати довірчий інтервал для прогнозних значень результуючої змінної;

3) отримані за 1МНК оцінки параметрів регресії будуть незміщеними, обгрунтованими, але неефективними. Тобто наявність гетероскедастичності спричиняє порушення властивостей оцінок параметрів моделі при розрахунку їх за методом 1МНК. А отже, при використанні звичайних процедур перевірки гіпотез висновки можуть бути неправильними.

Тому завжди виникає необхідність вивчати це явище, і, якщо воно існує, для оцінки параметрів моделі використовувати узагальнений метод найменших квадратів (метод Ейткена).

Як і в разі мультиколінеарності, єдиних правил виявлення гетероскедастичності немає, а є різноманітні тести (критерії). Для виявлення гетероскедастичності зазвичай використовують тести, в яких робляться різні припущення про залежність між дисперсією вільного члену та пояснюючою змінною, наприклад:

1) критерій m;

2) параметричний та непараметричний тести Голдфельда-Квандта;

3) тест рангової кореляції Спірмена;

4) двосторонній критерій Фішера;

5) тест Глейсера.

Варто відмітити, що умова означає, що дисперсія істинної похибки є постійною величиною на будь-якому з відрізків інтервалу, що розглядається. У зв’язку з цим перевірка даної умови може бути ідентичною перевірці гіпотези про постійність дисперсії фактичної похибки на різних відрізках інтервалу.

6.2 Методи визначення гетероскедастичності

В ході проведення дослідження гетероскедастичність або вгадується інтуїтивно, або висувається як абсолютне припущення. Отже, перший крок до виявлення гетероскедастичності – глибокий аналіз змісту проблеми, що досліджується. Крім того, існує графічний метод тестування наявності гетероскедастичності, що ґрунтується на встановленні наявності систематичного зв’язку квадратів залишків регресійної моделі , побудованої на основі припущення про відсутність гетероскедастичності (графічний аналіз).

6.2.1 Тест Голдфельда-Квандта

Для оцінки гетероскедастичності може використовуватися параметричний тест Голдфельда-Квандта. Даний тест використовується для перевірки такого типу гетероскедастичності, коли дисперсія залишків збільшується пропорційно квадрату фактора. При цьому робиться припущення, що випадкова складова розподілена нормально.

Основні кроки тесту:

1) упорядкувати спостережень по мірі збільшення змінної , залежність залишків з якою припускається;

2) виключити середніх спостережень ( повинно приблизно дорівнювати чверті (1/4) загальної кількості спостережень);

3) розділити сукупність на дві групи (відповідно з малими та великими значеннями фактору ) та визначити по кожній з груп рівняння регресії;

4) визначити залишкову суму квадратів для першої регресії 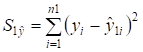та другої регресії ;

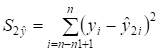5) вирахувати відношення (або ). В чисельнику повинна бути більша сума квадратів;

6) отримане відношення має F-розподіл зі ступенями вільності і (де  – число параметрів в рівнянні регресії, що оцінюється;  – число спостережень в першій групі).

Якщо 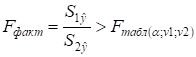, то гетероскедастичність має місце.

Приклад.

Застосуємо тест Голдфельда-Квандта для перевірки наявності гетероскедастичності залишків. Тестом перевіряється за критерієм Фішера основна гіпотеза H₀: при альтернативній гіпотезі H_α: не H₀. Для цього упорядкуємо вхідні дані, що відображають прибутки банків України (Y, млн.грн.) та величини їх статутного фонду (X, млн.грн.) в порядку спадання значень пояснюючої змінної X (табл. 6.1).

Таблиця 6.1

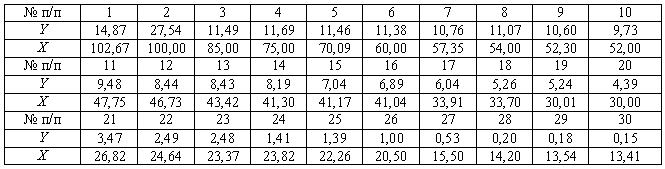
Відкинемо () середніх спостережень (друга підвибірка), вважаючи, що дисперсія залишків для них постійна. За методом найменших квадратів знайдемо оцінки параметрів спочатку для першої моделі (підвибірка 1) з найбільшими значеннями регресора X, потім для другої – з найменшими значеннями X ( третя підвибірка).

Знайдемо значення та (табл. 6.2) для першої та другої моделей та перевіримо наявність гетероскедастичності залишків на основі тесту Гольдфельда-Квандта.

Таблиця 6.2

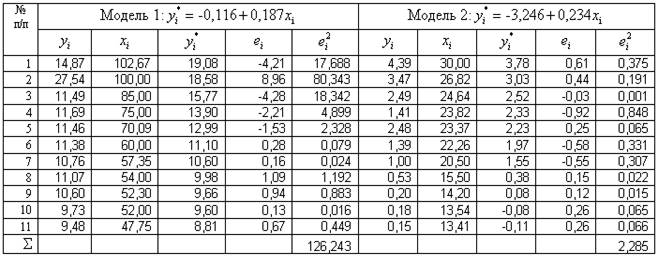
Для цього обчислимо суми квадратів залишків 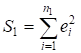і 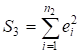та розрахуємо значення .

Розраховане значення 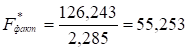порівняємо з табличним значенням =3,18 із ступенями свободи k₁=11-1-1=9 і k₂=11-1-1=9 при рівні значущості α=0,05. Так як >, гіпотезу H₀ про відсутність гетероскедастичності залишків відхиляємо.

6.2.2 Тест рангової кореляції Спірмена

У випадку гетероскедастичності абсолютні залишки корельовано зі значенням фактору . Цю кореляцію можна виміряти за допомогою коефіцієнта рангової кореляції Спірмена:

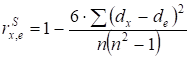, (6.4)

де  – ранги показників ;

 – число пар, що корелюють.

6.2.3 Тест Глейсера

Ще один тест для перевірки гетероскедастичності склав Глейсер. Він запропонував розглядати регресію абсолютних значень залишків , що відповідають регресії найменших квадратів, як певну функцію від , де  – та незалежна змінна, яка відповідає зміні дисперсії . Для цього використовуються такі види функцій:

1)

2)

3) і т.ін.

Рішення про відсутність гетероскедастичності залишків приймається на підставі статистичної значущості коефіцієнтів і .

Переваги цього тесту визначаються можливістю розрізняти випадок чистої і замішаної гетероскедастичності. Чистій гетероскедастичності відповідають значення параметрів , а змішаній — . Залежно від цього треба користуватись різними матрицями S. Нагадаємо, що .

6.3 Трансформування початкової моделі

Розглянемо питання усунення гетероскедастичності трансформуванням початкової моделі.

Припустимо. що за статистичними даними побудовано початкову регресійну модель

і на базі будь-якого тесту встановлено наявність гетероскедастичності.

Трансформація моделі зводиться до зміни початкової форми моделі методом, який залежить від специфічної форми гетероскедастичності. тобто від форми залежності між дисперсіями залишків і значеннями незалежних змінних

.

Приклад. Нехай початкова модель має вигляд

.

Припустимо, що гетероскедастичність має форму

,

де (тобто дисперсія залишків зростає пропорційно до ).

Із припущення випливає, що .

Це означає, що допустима трансформація полягає в діленні початкової моделі на .

Отже, трансформована модель має вигляд

.

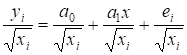Розглянемо

.

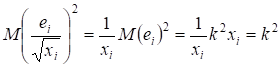Отже, для трансформованої моделі випадкова величина гомоскедастична зі сталою дисперсією . Це означає, що, виконавши зазначене вище перетворення, ми виключили гетероскедастичність.

Загальний випадок.

Припустимо, що гетероскедастичність має форму:

.

Трансформація початкової моделі здійснюється діленням іі на .

Зазначимо, що така трансформація еквівалентна застосуванню зваженого методу найменших квадратів (ЗМНК), який є особливим випадком узагальненого методу найменших квадратів (УМНК). Суть ЗМНК полягає в мінімізації зваженої суми квадратичних відхилень:

.

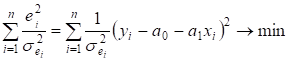ЗМНК, застосований до початкової моделі дає такі ж результати, що і застосування МНК до трансформованої моделі.

Оцінки трансформованої модлеі мають меншу дисперсію (ефективніші) ніж оцінки, отримані із застосуванням МНК до початкової моделі.

Також потрібно пам’ятати, що гетероскедастичність може існувати за рахунок неврахованих в моделі факторів. У цьому разі можливим рішенням є їх включення. Застосування трансформації без аналізу причин гетероскедастичності зробить гомоскедастичною випадкову змінну , однак оцінки параметрів можуть залишитися неправильними.

6.4 Узагальнений метод найменших квадратів (метод Ейткена)

За наявності гетероскедастичності для оцінювання параметрів моделі доцільно застосовувати узагальнений метод найменших квадратів (метод Ейткена), вектор оцінювання якого має вигляд:

.

Вектор а містить незміщену лінійну оцінку параметрів моделі, яка має найменшу дисперсію і матрицю коваріацій:

.

Для отримання УМНК-оцінок необхідно знати коваріаційну матрицю S вектора похибок, яка на практиці дуже рідко відома. Тому природно спершу оцінити матрицю S, а потім застосувати її оцінку у формулах. Цей підхід є суттю УМНК.

Оскільки явище гетероскедастичності пов’язане лише з тим, що змінюються дисперсії залишків, а коваріація між ними відсутня, то матриця S має бути діагональною, а саме:

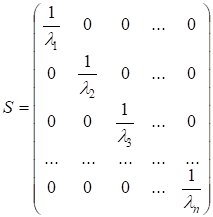
Щоб пояснити, чому саме такий вигляд має ця матриця, потрібно ще раз наголосити: за наявності гетероскедастичності для певних вихідних даних одна (або кілька) пояснювальних змінних можуть різко змінюватись від одного спостереження до іншого, тоді як залежна змінна має такі самі коливання, як і для попередніх спостережень.

Але це означає, що дисперсія залишків, яка змінюватиметься від одного спостереження до іншого (чи для групи спостережень), може бути пропорційною до величини пояснювальної змінної X (або до її квадрата), яка зумовлює гетероскедастичність, або пропорційною до квадрата залишків.

Звідси в матриці S значення можна обчислити, користуючись гіпотезами:

а) , тобто дисперсія залишків пропорційна до зміни пояснювальної змінної ;

б) , тобто зміна дисперсії пропорційна до зміни квадрата пояснювальної змінної ();

в) , тобто дисперсія залишків пропорційна до зміни квадрата залишків за модулем.

Для першої гіпотези: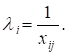

Для другої гіпотези: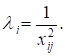

Для третьої гіпотези: або , або .

Оскільки матриця S – симетрична і додатньо визначена, то при , матриця P має вигляд:

.

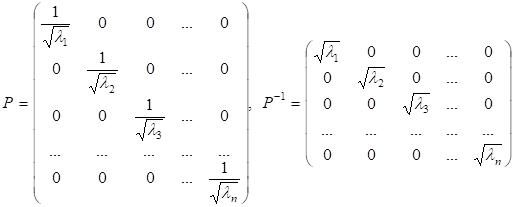При цьому коефіцієнт детермінації не може бути задовільною мірою якості моделі у випадку застосування УМНК. У загальному випадку його значення навіть не повинно перебувати в межах , а додавання чи вилучення незалежної змінної не обов’язково зумовлює його збільшення чи зменшення.

7.1 Природа автокореляції та її наслідки

Автокореляція – це взаємозв’язок послідовних елементів часового чи просторового ряду даних.

В економетричних дослідженнях часто зустрічаються такі випадки, коли дисперсія залишків є постійною, але спостерігається їх коваріація. Це явище має назву автокореляції залишків. В економетричних моделях автокореляція залишків має особливе значення, оскільки при її наявності порушується одна з умов, що висуваються при оцінці параметрів моделі за методом 1МНК.

Автокореляція залишків виникає найчастіше тоді, коли економетрична модель будується на основі часових рядів. Якщо існує кореляція між послідовними значеннями деякої незалежної змінної, то спостерігатиметься й кореляція послідовних значень залишків, так звані лагові затримки (запізнювання) в економічних процесах.

Тобто в цьому випадку також порушується гіпотеза, згідно з якою але при гетероскедастичності змінюється дисперсія залишків при відсутності їх коваріації, а при автокореляції – існує коваріація залишків при незмінній дисперсії.

При автокореляції залишків, як і при гетероскедастичності дисперсія залишків запишеться:

(7.1)

але матриця матиме тут зовсім інший вигляд. Запишемо цю матрицю:

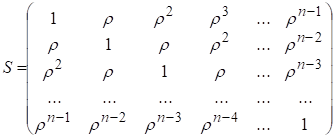. (7.2)

В даній матриці параметр r характеризує коваріацію кожного наступного значення залишків із попереднім. Так, якщо для залишків записати авторегресійну модель першого порядку:

, (7.3)

то r характеризує силу зв’язку величини залишків у період t від величини залишків у період t – 1.

Якщо проігнорувати матрицю при визначенні дисперсії залишків, і для оцінки параметрів моделі застосувати метод 1МНК, то можливі такі наслідки:

1) оцінки параметрів моделі можуть бути незміщеними, але неефективними, тобто вибіркові дисперсії вектора оцінок можуть бути невиправдано великими;

2) статистичні критерії t і F- статистики, які отримані для класичної лінійної моделі, практично не можуть бути використані для дисперсійного аналізу, бо їх розрахунок не враховує наявності коваріації залишків;

3) неефективність оцінок параметрів економетричної моделі, як правило, призводить до неефективних прогнозів, тобто прогнозні значення матимуть велику вибіркову дисперсію.

Автокореляція може виникати через інерційність і циклічність багатьох економічних процесів. Провокувати автокореляцію також може неправильно специфікована функціональна залежність у регресійних моделях. Наприклад, модель може не включати істотній фактор, яким часто виступає фактор часу.

При чому важливо відрізняти від істинної автокореляції залишків випадки неправильної специфікації моделі. Оскільки в останньому випадку необхідно змінити форму моделі. При цьому можуть використовуватися різні методи усунення автокореляції, наприклад:

-        введення у модель фактору часу;

-        перехід до темпових чи відносних показників;

-        включення у модель неврахованих факторів;

-        побудова авто регресійних рівнянь.

У випадку ж істинної автокореляції залишків застосовують спеціальні методи оцінки параметрів регресії з автокорельованими залишками.

7.2 Методи визначення автокореляції

Тестування наявності автокореляції, як правило, здійснюється за d-тестом Дарбіна-Уотсона, хоча існують й інші не менш відомі тести: критерій фон Неймана, нециклічний коефіцієнт автокореляції, циклічний коефіцієнт автокореляції.

7.2.1 Критерій Дарбіна-Уотсона

Cкладається з кількох етапів і включає зони невизначеності.

Крок 1. Розраховується значення d-статистики за формулою

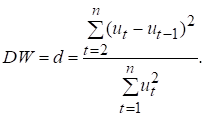(7.4)

Доведено, що значення d-статистики Дарбіна-Уотсона перебуває в межах 0 < DW < 4.

Крок 2. Задаємо рівень значущості a. За таблицею Дарбіна-Уотсона при заданому рівні значущості a, кількості факторів m і кількості спостережень n знаходимо два значення DW₁ і DW₂:

-        якщо 0< DW<DW₁, то наявна додатна автокореляція;

-        якщо DW₁ <DW< DW₂ або 4-DW₂< DW < 4-DW₁, то ми не можемо зробити висновки ані про наявність, ані про відсутність автокореляції (DW потрапляє в зону невизначеності);

-        якщо 4-DW₁ < DW < 4, маємо від’ємну автокореляцію;

-        якщо DW₂ < DW < 4-DW₂, то автокореляція відсутня.

Графічне зображення розподілу ілюструє рис. 7.1.

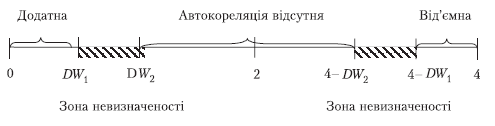
Рисунок 7.1 – Зони автокореляційного зв’язку за критерієм Дарбіна-Уотсона

Тест Дарбіна-Уотсона можна застосовувати лише в тому випадку, якщо:

а)      в регресійному рівнянні присутній вільний член;

б)      регрессори є нестохастичними;

в)      в регресійному рівнянні немає лагових значень залежної змінної.

7.2.2 Критерій фон Неймана

Для виявлення автокореляції залишків використовується також критерій фон Неймана:

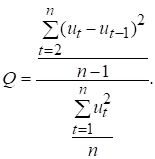(7.5)

Звідси . При . Фактичне значення критерію фон Неймана порівнюється з табличним для вибраного рівня значущості і заданого числа спостережень. Якщо , то існує додатна автокореляція.

7.2.3 Коефіцієнти автокореляції та їх застосування

Цей коефіцієнт виражає ступінь взаємозв’язку залишків кожного наступного значення з попереднім, а саме:

I ряд – ;

II ряд – .

Він обчислюється за формулою:

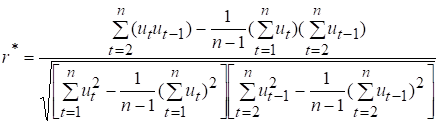(7.6)

Коефіцієнт може набувати значень в інтервалі (–1;+1). Від’ємні значення його свідчать про від’ємну автокореляцію, додатні – про додатну. Значення, що містяться в деякій критичній області біля нуля, свідчать про відсутність автокореляції, тобто стверджують нульову гіпотезу про відсутність автокореляції залишків. Оскільки ймовірнісний розподіл встановити трудно, то на практиці замість обчислюють циклічний коефіцієнт автокореляції .

Загалом, якщо часовий ряд має циклічний характер, тобто припускається, що після значення загальний характер зміни членів ряду повторюється, то автокореляцію визначають за допомогою коефіцієнта r⁰, запровадженого Андерсоном.

У цьому разі автокореляція визначається між послідовностями, зсунутими на період t:

Якщо період t=1, то маємо коефіцієнт циклічної автокореляції першого порядку, який відбиває інтенсивність взаємозв’язку між послідовностями:

I ряд – , ;

II ряд – , .

Циклічний коефіцієнт обчислюється за формулою:

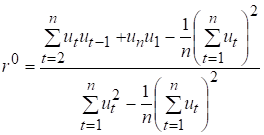(7.7)

Для досить довгих рядів вплив циклічних членів на величину коефіцієнта незначний, тому можна вважати, що ймовірнісний розподіл наближається до розподілу . Якщо останній член ряду дорівнює першому, тобто u₁ = u_n, то нециклічний коефіцієнт автокореляції дорівнює циклічному. Очевидно, що коли залишки не містять тренду, то припущення про рівність u₁ = u_n недалеке від реальності і циклічний коефіцієнт автокореляції наближається до нециклічного.

Фактично обчислене значення циклічного коефіцієнта автокореляції порівнюється з табличним для вибраного рівня значущості і довжини ряду n. Якщо , то існує автокореляція. Припускаючи, що 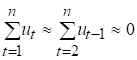, циклічний коефіцієнт автокореляції можна записати у вигляді

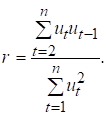(7.8)

На практиці часто замість (7.8) обчислюють

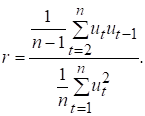(7.9)

Аналогічно можна визначити коефіцієнти другого та більш високого порядків (в формулах 7.6-7.9 замість використовують , а сумують починаючи не з 2, а з ).

Число періодів, за якими розраховується коефіцієнт автокореляції, називається лагом. Однак, зі збільшенням лагу число пар значень, по яким розраховується коефіцієнт, зменшується. Вважається доцільним для забезпечення статистичної достовірності коефіцієнтів використовувати правило, що максимальний лаг не повинен перевищувати n/4.

Властивості коефіцієнта автокореляції:

1) він характеризує тісноту лінійного зв’язку поточного та попередніх рівнів ряду і при наявності сильного нелінійного зв’язку може прямувати до 0;

2) по знаку коефіцієнта кореляції не можна робити висновок про зростаючу чи спадну тенденцію в рівнях ряду; більшість часових рядів економічних даних містять додатну автокореляцію рівнів, але при цьому можуть мати спадну тенденцію.

Послідовність коефіцієнтів автокореляції рівнів першого, другого та наступних порядків називають автокореляційною функцією часового ряду. Графік залежності її значень від величини лагу називається корелограмою. За даними функцією та графіком можна визначити структуру ряду.

Приклад.

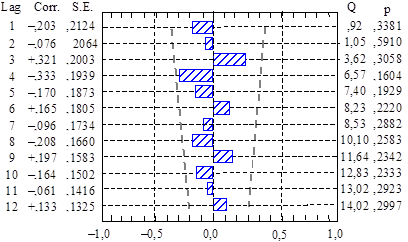
Рисунок 2 – Корелограма ряду залишків (побудовано в ПП Statistica)

На графіку точками позначено дві симетричні прямі, які визначають 95 %-ві межі значущості коефіцієнта автокореляції (± дві стандартні похибки, тобто = 0,417, де n = 24. Точніше, n = 23 за k = 1 i n = 22 за k = 2 тощо). Оскільки жоден із коефіцієнтів автокореляції не лежить за цими межами, а в зміні значень коефіцієнтів відсутня певна закономірність, можна вважати, що в цьому разі ряд залишків не містить систематичної складової.

7.3 Оцінка параметрів моделі з автокорельованими залишками

Оцінку параметрів моделі з автокорельованими залишками можна виконувати на основі чотирьох методів:

1) Ейткена;

2) перетворення вихідної інформації;

3) Кочрена-Оркатта;

4) Дарбіна.

Перші два методи доцільно застосовувати тоді, коли залишки описуються авторегресійною моделлю першого порядку (7.3).

Ітераційні методи Кочрена-Оркатта і Дарбіна можна застосовувати для оцінки параметрів економетричної моделі також і тоді, коли залишки описуються авторегресійною моделлю вищого порядку:

. (7.10)

7.3.1 Метод Ейткена (УМНК)

Як зазначалося, оператор оцінювання УМНК можна записати так:

(7.11)

де  – вектор оцінок параметрів економетричної моделі;

 – матриця, обернена до матриці кореляції залишків;

 – матриця, обернена до матриці V, де , а  – залишкова дисперсія.

Звідси

(7.12)

Отже, щоб оцінити параметри моделі на основі методу Ейткена, треба сформувати матрицю S (7.2).

У цій симетричній матриці виражає коефіцієнт автокореляції s-го порядку для залишків . Очевидно, що коефіцієнт автокореляції нульового порядку дорівнює 1.

Оскільки коваріація залишків при s > 2 часто наближається до нуля, то матриця, обернена до матриці S, матиме такий вигляд:

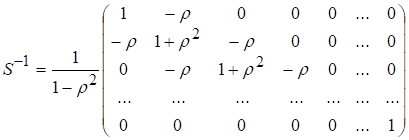(7.13)

Таку матрицю іноді пропонується використовувати при оцінюванні параметрів моделі з автокорельованими залишками за методом Ейткена.

При цьому для обчислення r використовується циклічний коефіцієнт кореляції r, розрахований за формулою (7.8) або (7.9).

Зауважимо, що параметр r (або ) має зміщення. Тому, використовуючи такий параметр для формування матриці S, необхідно скоригувати його на величину зміщення

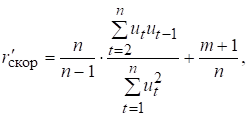(7.14)

де  – величина зміщення (m – кількість незалежних змінних).