ПРАКТИЧНА
РОБОТА №6
Тема:
ЗАСТОСУВАННЯ
ТЕОРІЇ ЧАСОВИХ РЯДІВ ДЛЯ АНАЛІЗУ ТА ПРОГНОЗУ ЕКОНОМІЧНИХ ПРОЦЕСІВ
Мета роботи: аналіз
поведінки часового ряду та розробка на його основі прогнозу реальних
економічних процесів та систем.
Зміст роботи: провести
попередній аналіз рядів динаміки та їх ідентифікацію. Здійснити аналітичне
вирівнювання ряду адаптивними методами, побудувати модель часового ряду та
зробити на її основі прогноз даних.
Вимоги до звіту: назва, тема, мета, завдання, вихідні дані варіанту. Результати
аналітичного розв’язання задачі та комп’ютерного у вигляді таблиці MS Excel з
вихідними умовами експерименту, таблиці MS Excel з результатами обчислень,
висновок про отримані результати. Опис інструментів та функцій MS Excel, що
використовувались при вирішенні задачі. Короткий опис технології вирішення
задачі в MS Excel.
ТЕОРЕТИЧНІ АСПЕКТИ
Адаптивні методи
прогнозування застосовуються в ситуації зміни зовнішніх умов,
коли найбільш важливими стають останні реалізації досліджуваного процесу.
Загальна схема побудови адаптивних методів може бути подана так:
1) за
кількома першими рівнями ряду будується модель і оцінюються її параметри;
2) на
основі побудованої моделі розраховується прогноз на один крок вперед, причому
його відхилення від фактичного рівня ряду розцінюється як помилка
прогнозування, яка враховується відповідно до прийнятої схеми коригування
моделі;
3) за
моделлю з відкоригованими параметрами розраховується прогнозна оцінка на
наступний момент часу тощо.
Схему такого
процесу представлено на рис. 5.3.
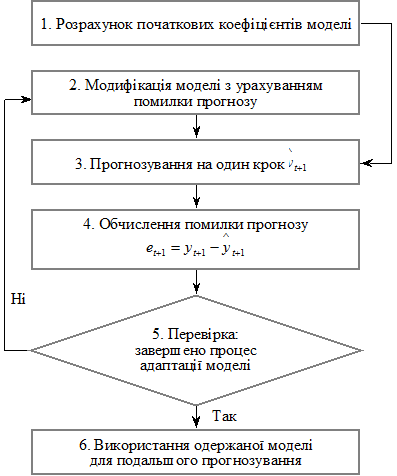
Рисунок
5.3 – Схема побудови адаптивних моделей
Після
надходження фактичного значення обчислюється помилка, розбіжність між фактичним
і прогнозованим рівнем (довготермінова функція моделі): ![]() .
.
У моделі
передбачається, що зміна фактичного рівня є деякою часткою (![]() ) від очікуваної зміни
) від очікуваної зміни ![]() . Параметр
. Параметр ![]() називається
коригувальним коефіцієнтом або параметром адаптації. За критерій оптимальності
під час вибору параметра адаптації можна взяти мінімум середнього квадрата
помилок прогнозування. Чим ближчий
називається
коригувальним коефіцієнтом або параметром адаптації. За критерій оптимальності
під час вибору параметра адаптації можна взяти мінімум середнього квадрата
помилок прогнозування. Чим ближчий ![]() до одиниці, тим більше
сподівання економічних суб’єктів відповідають реальній динаміці часового ряду,
і навпаки, чим ближче до нуля – тим менше володіємо ситуацією, тому треба
вносити корективи.
до одиниці, тим більше
сподівання економічних суб’єктів відповідають реальній динаміці часового ряду,
і навпаки, чим ближче до нуля – тим менше володіємо ситуацією, тому треба
вносити корективи.
Таким чином,
модель постійно вбирає в себе нову інформацію і до кінця періоду навчання
відбиває тенденцію розвитку процесу, що існує на даний момент. Прогноз
отримується як екстраполяція останньої тенденції. Численні адаптивні методи
відрізняються один від одного лише способами числової оцінки параметрів моделі
і визначення параметрів адаптації. Базовими адаптивними методами вважаються
методи Хольта, Брауна і Хольта-Уїнтерса.
Модель Брауна
Якщо є часовий
ряд спостережень ![]() , то прогноз в момент часу t на
, то прогноз в момент часу t на ![]() кроків вперед можна
здійснити за формулою
кроків вперед можна
здійснити за формулою
![]() (5.19)
(5.19)
де ![]() – поточні оцінки коефіцієнтів адаптивного поліному.
– поточні оцінки коефіцієнтів адаптивного поліному.
В моделі Брауна
модифікація (адаптація) коефіцієнтів лінійної моделі здійснюється наступним
чином
![]() ,
, ![]() (5.20)
(5.20)
де ![]() – коефіцієнт дисконтування даних,
– коефіцієнт дисконтування даних,
![]() – похибка прогнозу (
– похибка прогнозу (![]() ).
).
Початкові
значення параметрів моделі можна визначити за методом МНК на основі декількох
перших спостережень. Оптимальне значення параметра дисконтування знаходиться в
межах [0;1], визначається методом чисельної оптимізації і є постійним для
всього періоду спостережень. За рахунок оператору В можна зрушувати всю
послідовність на один крок назад: ![]() . Застосування оператору В до спостережень і до коефіцієнтів
адаптивного поліному дозволяє виразити модель Брауна у вигляді
. Застосування оператору В до спостережень і до коефіцієнтів
адаптивного поліному дозволяє виразити модель Брауна у вигляді
![]() . (5.21)
. (5.21)
Тоді модель
Брауна можна трактувати як модель авторегресії ARIMA (0, 2, 2)-моделлю: ![]() з коефіцієнтами
ковзної середньої –
з коефіцієнтами
ковзної середньої – ![]() та
та ![]() .
.
Точковий прогноз
розраховують після підстановки значення ![]() в оцінювану модель.
Межі інтервалу надійності прогнозу можна визначити за формулою:
в оцінювану модель.
Межі інтервалу надійності прогнозу можна визначити за формулою:
![]() , (5.22)
, (5.22)
де величини ![]() .
.
ПРАКТИЧНІ
ЗАВДАННЯ
Дати характеристику структури
часового ряду, використовуючи графічне зображення.
2. Здійснити аналітичне вирівнювання ряду адаптивними методами та
розрахувати трендову складову. З цією метою застосувати
модель Брауна для ex post прогнозу на 6
періодів вперед. Початкові значення параметрів моделі визначити за методом МНК
на основі 100 (180) перших спостережень. Параметр дисконтування початковий
встановити на рівні 0,5.
3. Провести операції по розрахунку сезонної складової. Для цього
здійснити фільтрацію сезонної компоненти за допомогою індексу сезонності,
використавши значення періоду сезонності 12 та адитивну тренд-сезонну модель.
4. Оцінити якість прогнозу
Початкові дані:
Згідно порядкового номеру студента в списку групи вибрати
початкові дані для подальшої обробки з файлу Варіанти завдань до ПР.06.xlsx.
КОНТРОЛЬНІ
ПИТАННЯ
1.
Яку структуру може
мати часовий ряд?
2.
Які особливості має
часовий ряд на відміну від ряду просторових даних?
3.
Який ряд
називається стаціонарним?
4.
Яким чином
здійснюється фільтрація компонент часового ряду?
5.
Що означає ідентифікувати часовий ряд за допомогою автокореляційного аналізу?
6.
Як визначається
трендова компонента часового ряду?
7.
В чому полягає суть
адаптивних методів вирівнювання ряду?
8.
Яким чином
визначається параметр дисконтування в моделі Брауна?
9.
Якими методами
визначається сезонна компонента часового ряду?
10.
Чи наявна в
часовому ряді сезонна компонента? Обґрунтуйте.
11.
Класифікуйте
побудовану модель часового ряду.
12.
Яким чином
здійснюється перевірка якості та точності побудованої моделі?
13.
Якими методами може
оцінюватися якість прогнозів за розробленою моделлю часового ряду?

