1.3.3. Фрикційні властивості одиничних матеріалів
При
спробі зсунути рослинний матеріал відносно поверхні, до якої він притискається,
або відносно іншого матеріалу, необхідно перебороти силу тертя. При переміщенні
майже усіх видів рослинних матеріалах по поверхнях може мати місце тертя
ковзання, в окремих матеріалів, таких, як плоди, ягоди, насінневі коробочки,
зерно, насіння, при переміщенні можлива наявність тертя кочення, у ряді
випадків при переміщенні матеріалів можливе тертя гнучких тіл.
Тертя
ковзання може мати місце, якщо на матеріал, що лежить, наприклад, на
горизонтальній площині, діють сила ваги G
(рис. 1.7) і горизонтально прикладена рушійна сила P. Тут можливо кілька випадків, розглянемо їх.
Нехай
матеріал спочатку перебуває у спокої (рис. 1.7, а). Дія вертикально спрямованої сили G, прикладеної в центрі мас С,
викликає рівну їй і протилежно спрямовану (тобто вверх) реакцію N
опорної площини. Таким чином, N=G.
Прикладемо тепер до матеріалу ліворуч рушійну силу P; якщо ця сила мала, то вона не зможе зрушити матеріал вправо.
Перебування матеріалу на площині в спокої означає, що площина діє на матеріал
із силою, що врівноважує дію сили P .
Позначимо цю силу F . Це сила тертя,
вона діє на матеріал у місцях його контакту з площиною. Оскільки сила F
врівноважує силу P, це можна
записати: F=P. Склавши геометрично
сили реакцій N (нормальна) і F (дотична), одержимо рівнодійну R, рівну![]() і відхилену від сили N на кут α, тангенс якого
рівний:
і відхилену від сили N на кут α, тангенс якого
рівний: ![]() .
.
Будемо
тепер збільшувати силу P і домагатися
такого положення, щоб матеріал почав рухатися. Позначимо силу P, при дії якої матеріал починає
рухатися, через ![]() (рис. 1.7, б), а
рівну їй і протилежно спрямовану силу
тертя через
(рис. 1.7, б), а
рівну їй і протилежно спрямовану силу
тертя через ![]() . Ця сила називається силою тертя спокою, це максимально
можлива сила тертя в зоні контакту матеріалу з площиною. З викладеного випливає, що
. Ця сила називається силою тертя спокою, це максимально
можлива сила тертя в зоні контакту матеріалу з площиною. З викладеного випливає, що ![]() . Склавши геометрично сили реакцій N і
. Склавши геометрично сили реакцій N і ![]() , одержимо рівнодійну R,
рівну
, одержимо рівнодійну R,
рівну![]() і відхилену від сили N на кут
і відхилену від сили N на кут ![]() , тангенс якого рівний:
, тангенс якого рівний: ![]() , де
, де ![]() – кут тертя спокою. З
представленої рівності випливає, що
– кут тертя спокою. З
представленої рівності випливає, що ![]() . Позначимо
. Позначимо ![]() через
через ![]() , ця величина називається коефіцієнтом тертя спокою. Таким
чином
, ця величина називається коефіцієнтом тертя спокою. Таким
чином
![]() . (1.4)
. (1.4)
Кут ![]() більший кута
більший кута ![]() , зображеного на рис. 1.7, а.
, зображеного на рис. 1.7, а.
Як
показують досліди, для підтримки подальшого рівномірного руху матеріалу (по
площині) потрібна сила Р, трохи
менша, ніж ![]() . Позначимо її
. Позначимо її ![]() . Ми можемо тепер
записати, що при рівномірному русі матеріалу
. Ми можемо тепер
записати, що при рівномірному русі матеріалу ![]() . Позначимо силу тертя, що
врівноважує дію сили
. Позначимо силу тертя, що
врівноважує дію сили![]() , через
, через ![]() . Це сила тертя ковзання. Вона, як бачимо, трохи
менша, ніж
. Це сила тертя ковзання. Вона, як бачимо, трохи
менша, ніж ![]() . Сили
. Сили ![]() і
і ![]() показані на
рис. 1.7, в. На основі
викладеного приходимо до наступної рівності:
показані на
рис. 1.7, в. На основі
викладеного приходимо до наступної рівності: ![]() . Склавши геометрично сили реакцій N і
. Склавши геометрично сили реакцій N і ![]() , отримаємо рівнодіючу R,
рівну
, отримаємо рівнодіючу R,
рівну![]() і відхилену від сили N на кут
і відхилену від сили N на кут ![]() , тангенс якого рівний:
, тангенс якого рівний: ![]() , де
, де ![]() - кут тертя ковзання. З представленої рівності випливає, що
- кут тертя ковзання. З представленої рівності випливає, що ![]() . Позначимо
. Позначимо ![]() через
через ![]() , ця величина називається коефіцієнтом тертя ковзання. Тоді
, ця величина називається коефіцієнтом тертя ковзання. Тоді
![]() . (1.5)
. (1.5)
Кут ![]() трохи менший кута
трохи менший кута ![]() , а коефіцієнт
, а коефіцієнт ![]() також трохи менший
коефіцієнта
також трохи менший
коефіцієнта ![]() .
.
Якщо ж
сила Р більша сили ![]() (рис. 1.7, г), то матеріал буде рухатися з
прискоренням, рівним
(рис. 1.7, г), то матеріал буде рухатися з
прискоренням, рівним ![]() , де
, де ![]() - маса
- маса
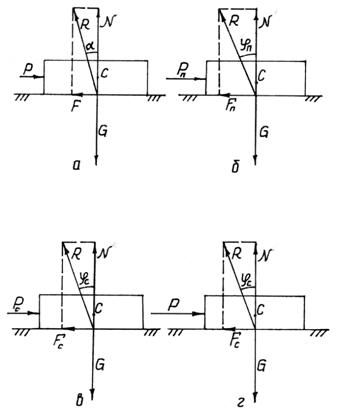
Рис. 1.7. Схеми, що пояснюють виникнення тертя при дії рушійної сили на матеріал, що знаходиться на нерухомій площині: а - матеріал не рухається; б - матеріал почав рухатися, переборюючи тертя спокою; в - матеріал рухається рівномірно і ковзає по площині; г - матеріал рухається прискорено і ковзає по площині
Кут ![]() трохи менший кута
трохи менший кута ![]() , а коефіцієнт
, а коефіцієнт ![]() також трохи менший
коефіцієнта
також трохи менший
коефіцієнта ![]() .
.
Якщо ж сила Р
більша сили ![]() (рис. 1.7, г), то матеріал буде рухатися з
прискоренням, рівним
(рис. 1.7, г), то матеріал буде рухатися з
прискоренням, рівним ![]() , де
, де ![]() - маса матеріалу. І в даному випадку, крім нормальної
реакції
- маса матеріалу. І в даному випадку, крім нормальної
реакції ![]() , на матеріал діє сила тертя
, на матеріал діє сила тертя ![]() , про яку вище говориться, значить рівнодійна
, про яку вище говориться, значить рівнодійна ![]() визначається за наведеним
вище виразом
визначається за наведеним
вище виразом![]() і відхилена на кут
і відхилена на кут ![]() від сили
від сили ![]() .
.
Тертя спокою називається ще статичним тертям, а тертя
ковзання називається динамічним тертям. Через невелику різницю у величинах ![]() і
і ![]() на практиці часто не роблять розходження між ними і пишуть
на практиці часто не роблять розходження між ними і пишуть ![]() (замість
(замість ![]() або
або![]() ), однак є багато
випадків, де ці розходження повинні бути враховані.
), однак є багато
випадків, де ці розходження повинні бути враховані.
Слід зазначити, що параметри ![]() і
і ![]() не є постійними величинами, вони залежать від розмірів
дотичних поверхонь, чистоти їхньої обробки, швидкості руху однієї поверхні
відносно іншої, наявності шару змащення між поверхнями й іншими факторами.
Незважаючи на це, залежності (1.4) і (1.5) набули значного застосування в
інженерних розрахунках.
не є постійними величинами, вони залежать від розмірів
дотичних поверхонь, чистоти їхньої обробки, швидкості руху однієї поверхні
відносно іншої, наявності шару змащення між поверхнями й іншими факторами.
Незважаючи на це, залежності (1.4) і (1.5) набули значного застосування в
інженерних розрахунках.
Значення коефіцієнта тертя визначають за допомогою наступних приладів:
«похила площина»; конструкції акад. В. А. Желиговского; ПСТ, ДПТ і ПТСМ
конструкції ВИСХОМа й ін.
Прилад «похила площина» (рис. 1.8) містить основу 1, похилу площину 2, що повертається відносно основи,
і кутомір 4. Досліди з даним приладом проводять у наступному порядку.
Спочатку прилад установлюють горизонтально, до похилої площини зверху кріплять
один з досліджуваних матеріалів 3, а інший досліджуваний матеріал кріплять до
спеціального повзуна 5 або ж залишають у звичному стані. Повзун з матеріалом
або цей матеріал без повзуна розміщують на матеріалі похилої площини, після
чого площину плавно повертають однією
стороною вверх до початку ковзання по ній повзуна з матеріалом (або власне
матеріалу без повзуна). Зафіксований при цьому кут нахилу площини буде кутом
тертя спокою.

Рис. 1.8. Прилад «похила площина» для визначення
коефіцієнта тертя: 1 – основа; 2 – поворотна дошка; 3 – матеріал, що прикріплюється до дошки; 4 -
кутомір; 5 - повзун
Для визначення кута тертя ковзання відновлюють положення похилої площини,
при якому повзун з матеріалом (або безпосередньо матеріал без повзуна) ковзають
вниз, і одночасно плавно опускають похилу площину до зупинки на ній повзуна
(або другого матеріалу). Зафіксований при цьому кут буде кутом тертя ковзання.
Значення коефіцієнтів тертя ряду рослинних матеріалів по різних поверхнях
приведені в табл. 1.3. У таблиці приведені межі коливань коефіцієнтів
тертя, в основному, для матеріалів у повітряно-сухому стані. Конкретні значення
коефіцієнтів залежать від умов
виростання матеріалів, їхнього сорту, вологості, термінів збирання
й інших факторів. Зі збільшенням вологості матеріалів коефіцієнти
тертя зростають.
Різновидом тертя ковзання є тертя кручення, при якому розташовані в площині
дотику двох тіл точки одного тіла рухаються щодо іншого тіла по концентричних
колах з центром на осі, перпендикулярній площині дотику.
Табл. 1.3. Коефіцієнти тертя спокою і ковзання
ряду рослинних матеріалів
|
Назва рослинного матеріалу |
Поверхня
тертя |
Значення коефіцієнта тертя |
|
|
спокою (статичний) |
ковзання (динамічний) |
||
|
Пшениця, жито, ячмінь, рис,
кукурудза, овес, соняшник |
сталь |
0,36...0,58 |
0,33...0,48 |
|
дерево |
0,33...0,62 |
0,28...0,52 |
|
|
гума |
0,47...0,66 |
0,47...0,62 |
|
|
Просо, горох, вика, чечевиця,
насіння льону і коноплі |
сталь |
0,31...0,38 |
0,30...0,36 |
|
дерево |
0,33...0,41 |
0,33...0,40 |
|
|
гума |
0,36...0,44 |
0,38...0,48 |
|
|
Картопля, цибуля, буряк,
морква, ріпа |
сталь |
0,50...0,70 |
0,45...0,70 |
|
дерево |
0,55...0,78 |
0,48...0,75 |
|
|
гума |
0,60...0,90 |
0,57...0,90 |
|
|
Сіно і солома непресовані |
сталь |
0,25...0,35 |
0,24...0,39 |
|
дерево |
0,30…0,37 |
0,30...0,36 |
|
|
гума |
0,38...0,42 |
0,36...0,41 |
|
|
Свіжозібрані стебла льону |
сталь |
0,40...1,00 |
0,35...0,96 |
|
дерево |
0,50...0,60 |
0,48...0,59 |
|
|
гума |
0,60...0,90 |
0,56...0,90 |
|
|
Сухі стебла льону |
сталь |
0,20...0,40 |
0,20...0,38 |
|
дерево |
0,20...0,60 |
0,20...0,57 |
|
|
гума |
0,20...0,50 |
0,20...0,50 |
|
|
Листя |
сталь |
0,40...0,80 |
0,38...0,80 |
|
дерево |
0,50...1,00 |
0,47...0,98 |
|
|
гума |
0,80...1,20 |
0,80...1,20 |
|
|
Бавовна |
сталь |
0,45...0,55 |
0,45...0,53 |
|
дерево |
0,50...0,70 |
0,48...0,70 |
|
|
гума |
0,80...0,85 |
0,75...0,84 |
|
|
Плоди яблук |
сталь |
0,36...0,44 |
0,24...0,36 |
|
дерево |
0,38...0,48 |
0,25...0,40 |
|
|
гума |
0,55...0,70 |
0,40...0,60 |
|
|
Полова |
сталь |
0,31...0,57 |
0,30...0,55 |
|
дерево |
0,32...0,68 |
0,32...0,66 |
|
|
гума |
0,46...0,54 |
0,44...0,53 |
|
Тертя
кочення має місце, якщо на матеріал, що лежить на площині і має циліндричну
форму, діє сила таким чином, що викликає його кочення.
Схема
цього явища показана на рис. 1.9. На цій схемі на матеріал діє вертикально сила
ваги G, прикладена в центрі C кола, а по горизонталі також через
центр C діє сила P. Під дією зазначених сил у зоні контакту матеріалу з площиною
відбувається його деформація на ділянці DABE.
На цій ділянці площина тисне на матеріал, епюра тиску приблизно має вигляд,
представлений на схемі. Позначимо через R
результуючу цих сил тисків, вона прикладена в деякій точці В на відстані k від осі АС матеріалу. Відстань k називається коефіцієнтом тертя кочення
і вимірюється в одиницях довжини.
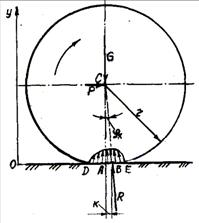
Рис. 1.9.
Сили, що діють на циліндр при його коченні по площині
При
рівномірному русі центру С матеріалу
сила R діє по лінії ВС, а діючі сили знаходяться в
рівновазі, тоді для визначення невідомих сил можна скласти рівняння рівноваги.
Проведемо вертикальну вісь Оу і
складемо рівняння проекцій сил на цю вісь і рівняння моментів сил відносно
точки А:
![]() ;
;
![]() ,
,
де ![]() – проекція сили R на вісь у, а СА – відстань від
точки С до точки А.
– проекція сили R на вісь у, а СА – відстань від
точки С до точки А.
Відстань СА
через деформацію циліндра трохи менша радіуса r циліндра, але ця різниця дуже мала і з метою спрощення
розрахунків будемо вважати,
що ![]() . Тоді, розв’язуючи рівняння
з урахуванням цієї наближеної рівності, отримаємо:
. Тоді, розв’язуючи рівняння
з урахуванням цієї наближеної рівності, отримаємо:
![]() . (1.6)
. (1.6)
Відношення  менше коефіцієнтів
тертя
менше коефіцієнтів
тертя  і
і  .
.
Якщо кут АСВ
позначити ![]() , то зі схеми видно, що
, то зі схеми видно, що ![]() . Кут
. Кут ![]() називається кутом
кочення. Цей показник застосовується для характеристики матеріалів, що мають
кулясту, циліндричну або еліпсоїдну форму. Кут jк рівний: jк=arcsin(k/r), де
r – радіус кривизни частини поверхні
матеріалу в точці її контакту з площиною, по якій він котиться. У бульб
картоплі jк = 16° при коченні по сталі і jк = 13° при коченні по гумі. У качанів кукурудзи при коченні по сталі jк = 15...18°, при коченні по дереву jк = 13...17°, а при коченні по гумі jк = 14...18.° У коренів редиски jк = 16°...18° по сталі і jк = 15...18° по дереву і гумі. У плодів помідорів jк = 12° по сталі і jк = 12...24° по гумі. У кавунів jк = 4...12° по сталі і дереву, а по гумі jк = 5...2.° У плодів яблук по сталі jк = 4...13°, коли яблуко котиться на боці, і jк = 9°...26°, коли яблуко котиться, знаходячись на чашечці або лійці.
називається кутом
кочення. Цей показник застосовується для характеристики матеріалів, що мають
кулясту, циліндричну або еліпсоїдну форму. Кут jк рівний: jк=arcsin(k/r), де
r – радіус кривизни частини поверхні
матеріалу в точці її контакту з площиною, по якій він котиться. У бульб
картоплі jк = 16° при коченні по сталі і jк = 13° при коченні по гумі. У качанів кукурудзи при коченні по сталі jк = 15...18°, при коченні по дереву jк = 13...17°, а при коченні по гумі jк = 14...18.° У коренів редиски jк = 16°...18° по сталі і jк = 15...18° по дереву і гумі. У плодів помідорів jк = 12° по сталі і jк = 12...24° по гумі. У кавунів jк = 4...12° по сталі і дереву, а по гумі jк = 5...2.° У плодів яблук по сталі jк = 4...13°, коли яблуко котиться на боці, і jк = 9°...26°, коли яблуко котиться, знаходячись на чашечці або лійці.
Тонкі вологі стебла цілком можуть бути віднесені
до гнучких тіл. Ковзання гнучких тіл по нерухомих скривлених напрямних
супроводжується появою значних по величині сил тертя. Розглянемо це явище.
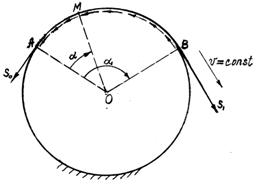
На рис. 1.10 представлена схема ділянки циліндричної
поверхні, по якій ковзає з постійною швидкістю ![]() гнучке тіло АВ, натягнуте з однієї сторони (у точці А) силою
гнучке тіло АВ, натягнуте з однієї сторони (у точці А) силою ![]() , а з іншого боку – силою
, а з іншого боку – силою ![]() . В міру руху тіла по циліндрі по дузі АМВ через подолання зображених невеликими дугами зі стрілками сил
тертя, спрямованих проти швидкості
. В міру руху тіла по циліндрі по дузі АМВ через подолання зображених невеликими дугами зі стрілками сил
тертя, спрямованих проти швидкості ![]() ковзання, сила натягу
гнучкого тіла збільшується. Відповідно до відомої формули Ейлера, виведеної за
умови, що гнучке тіло нерозтяжне, його твердість дорівнює нулю, швидкість
ковзання, сила натягу
гнучкого тіла збільшується. Відповідно до відомої формули Ейлера, виведеної за
умови, що гнучке тіло нерозтяжне, його твердість дорівнює нулю, швидкість ![]() постійна, а сили
інерції близькі до нуля, сила натягу тіла
постійна, а сили
інерції близькі до нуля, сила натягу тіла ![]() в точці М буде рівна:
в точці М буде рівна:
![]() (1.7)
(1.7)
де ![]() – основа
натуральних логарифмів;
– основа
натуральних логарифмів;
![]() – коефіцієнт тертя
ковзання;
– коефіцієнт тертя
ковзання;
![]() – кут АОМ.
– кут АОМ.
|
|
Рис. 1.10.
Ковзання натягнутого з двох сторін гнучкого тіла по поверхні циліндра |
У точці В сила натягу ![]() рівна:
рівна:
![]() (1.8)
(1.8)
де ![]() – кут АОВ.
– кут АОВ.
З викладеного випливає, що сила
тертя по дузі АМ рівна ![]() , а по дузі АМВ ця
сила тертя буде рівна
, а по дузі АМВ ця
сила тертя буде рівна ![]() .
.