3.1. Розтягування одиничних
матеріалів
Вище було сказано, що деформація розтягу
матеріалів має місце в багатьох процесах,
виконуваних сільськогосподар-
ськими машинами.
Дослідження закономірностей при
статичному розтягу рослин проводиться на экстензометрі (рис. 3.1). Можливе
застосування для цих досліджень інших приладів. Так, для дослідження розтягу
квітконіжок і відриву ягід були застосовані прилад і апаратура, представлені на
рис. 3.2. Для дослідження розтягу матеріалів при динамічних навантаженнях застосовуються
маятникові копри.
|
|
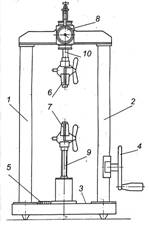
Рис. 3.1. Екстензометр
зі стеблом льону, що розтягується |
Екстензометр
(рис. 3.1 і 3.3) призначений для визначення міцності і відносних деформацій
частин рослин при розтягу (розриві), але може застосовуватися для дослідження
інших видів деформацій рослин.

Рис.
3.2. Вигляд приладу й апаратури для дослідження розтягу квітконіжок і відриву
ягід
Екстензометр
складається з двох стійок 1 і 2, панелі 3, маховика 4, лічильника 5, затискачів
6 і 7, індикатора 8, рухомого штока 9, нерухомого штока 10, зубчастої передачі
і плоскої силовимірювальної пружини.
|
|
Рис. 3.3. Екстензометр: 1 і 2 – стійки; 3 – панель; 4 – маховик; 5 – лічильник; 6
і 7 – затискачі; 8 – індикатор; 9 – рухливий шток; 10 – нерухомий шток |
Для дослідження розтягу рослини її кінці
затискаються в затискачах 6 і 7. Навантаження рослини відбувається за рахунок
передачі крутного моменту від маховика 4 через зубчасті передачі на шток 9, при
цьому шток із затискачем здійснює поступальний рух униз, впливаючи на зразок.
Деформація (переміщення рухомого штока з затискачем) фіксується лічильником,
причому зусилля, що впливає на зразок, передається на плоску силовимірювальну
пружину, деформація якої пропорційна зусиллю і фіксується індикатором годинникового
типу.
Використання плоских силовимірювальних пружин з різною
жорсткістю дозволяє змінювати зусилля навантаження в межах від 0 до 100 Н і від
20 до 200 Н. Похибка визначення деформацій досліджуваного зразка рослини
складає 0,01мм.
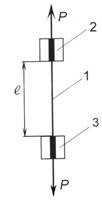
Схема навантаження стебла при його
розтягненні представлена на рис. 3.4, а.
Слід зазначити, що затиснення кінців стебла для його розтягу повинно бути
виконане в приладі так, щоб, з одного боку, одержати надійне затиснення цих
кінців, а з іншого боку, не пошкодити їх.
|
а |
б |
Рис. 3.4. Схема
навантаження (а) і діаграма розтягу
стебла (б): 1 – стебло; 2 і 3 – затискачі
При
проведенні досліджень визначається сила розтягу Р і відповідне їй видовження стебла Dl. За
цими даними, а також знаючи діаметр стебла d
і його початкову довжину l (точніше,
початкову відстань між затискачами), розраховуються відносні видовження стебла e і
умовне напруження s за формулами:
 (3.1)
(3.1)
Напруження
s називається умовним тому, що стебло має трубчасту будову і дійсна площа
поперечного перерізу менша ![]() . При конусній формі стебла параметр d буде являти собою діаметр найменшого січення в зоні розтягу.
Відносне видовження e може бути виражено не тільки у відносних величинах, але й у відсотках,
тоді
. При конусній формі стебла параметр d буде являти собою діаметр найменшого січення в зоні розтягу.
Відносне видовження e може бути виражено не тільки у відносних величинах, але й у відсотках,
тоді ![]() домножується на 100.
домножується на 100.
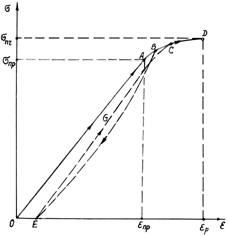
У
результаті дослідження була встановлена залежність напруження від відносної
деформації, представлена на рис. 3.4, б.
Діаграма в загальному випадку складається з прямолінійної ділянки ОА, на якій напруження пропорційне
подовженню (прямолінійна залежність), і ділянки ABCD, на якому деформація росте швидше, ніж напруження. Якщо на цій
ділянці в якій-небудь точці В
розвантажити стебло, то крива розвантаження буде мати вигляд BE, а повторне навантаження піде по
кривій EGC. В точці D стебло розривається. Ділянка ОА може на початку містити криволінійну
частину, якщо натягується скривлене стебло. Криволінійна ділянка ABCD для ряду культур дуже мала. У
крихких рослин він близький до нуля.
Відзначене
на діаграмі напруження sпр являє собою межу пропорційності, а величина eпр –
відповідне йому відносне видовження. Величини sпч і eр – це напруження і видовження, при якому відбувається розрив стебла.
Найбільше напруження sпч називається межею міцності (або тимчасовим опором). Оскільки стебло має
конічну форму, то при його розтягу розрив відбувається в зоні найменшого
діаметра, тобто там, де найбільш слабке січення. На прямолінійній ділянці ОА діаграми залежність s від e
підпорядковується закону Гука:
![]() , (3.2)
, (3.2)
де Е –
модуль деформації (відносно до металів це модуль пружності першого роду).
Обробкою
результатів дослідів і узагальненням результатів досліджень інших авторів
установлені значення Е і sпч, наведені в табл. 3.1. При
всіх інших рівних умовах модуль деформації тим більший, чим більший вік рослини
і її стиглість. Відносні видовження стебел при розриві eр незначні (0,01...0,05);sпр =(0,8...1,0)×sпр; eпр=(0,7...1,0)×eр. Слід зазначити, що розривне
зусилля стебел залежить від їхньої довжини. Із збільшенням довжини (а отже, і
їхнього діаметра) розривне зусилля істотно збільшується. З іншого боку, через
нерівномірне розташування пучків волокон по довжині стебла виходить, що чим
більша ця довжина, тим більше ослаблених місць і менша межа міцності.
Табл.3.1. Механічні характеристики ряду рослинних
матеріалів при статичному розтягу
|
Найменування
матеріалу |
Значення характеристик матеріалу |
Розривне зусилля однієї рослини, кН |
||
Е, кПа
|
sпч, кПа |
|||
|
Стебла |
Пшениці
і жита |
(5...20)×105 |
(1...4)×104 |
0,05...0,35 |
|
Рису |
(7...13)×104 |
(1...2)×103 |
0,10...0,50 |
|
|
Кукурудзи
і соняшника |
(5...15)×105 |
(1...2)×104 |
1...4 |
|
|
Льону-довгунця |
(3...6)×106 |
(2...8)×104 |
0,03...0,05 |
|
|
Коноплі |
(13...37)×104 |
(3...4)×104 |
0,42...0,80 |
|
|
Кенафу |
(1...2)×105 |
(3...4)×104 |
3...4 |
|
|
Бавовнику |
– |
200...500 |
– |
|
|
Бадилля |
Картопляна |
– |
100...200 |
0,20...0,49 |
|
Буряка |
– |
100...800 |
0,20...0,40 |
|
|
Моркви |
– |
10...30 |
0,12...0,23 |
|
|
Плодоніжки
яблук |
– |
40...80 |
0,15...0,25 |
|
Дослідженнями встановлено
також, що в рослин відношення залишкових деформацій до пружних зберігається
приблизно постійним, а межа пропорційності і межа міцності досить близькі одна
до одної. У рослин залишкові деформації виникають навіть при невеликих
навантаженнях і залежать від часу їхньої дії; у той же час рослини мають
відновну здатність аж до відновлення первісних розмірів з часом.
Межа міцності залежить від тривалості дії
навантаження; зі збільшенням цієї тривалості межа міцності зменшується.
Міцність стебел залежить від їхньої структури.
Модуль деформації більш зрілих стебел більший, ніж менш зрілих, а видовження –
навпаки. На ці фактори впливає і вміст вологи в стеблах – з його збільшенням
їхня міцність підвищується. Зусилля на розрив при динамічних навантаженнях
потрібно більше, ніж при статичних, міцність рослин менша при меншій їх
вологості.
Модуль деформації стебел льону і коноплі
зменшуються зі збільшенням їхньої вологості і зростає при їхньому дозріванні;
впливають на модуль і міцність стебел, а
також умови їхнього проростання. Стебла в міру свого розвитку спочатку
зміцнюються, а потім робляться більш слабкими. Розривне зусилля більше в стебел
більшого діаметра, а на самому стеблі руйнівне напруження більше у верхній його
частині.
Міцність прикріплення бульби картоплі до столона*
зменшується у процесі дозрівання рослин і по його висоті. Залежить вона від
сорту картоплі, грунтово-кліматичних умов і інших факторів. Найменш міцними
частинами куща є місця прикріплення
бульби до столона і столона до
стебла.
Розривне статичне
навантаження для плодоніжки кукурудзи складає 0,3...1,1 кН. Зі зменшенням
вологості плодоніжки кукурудзи зусилля на її розрив зменшується, а межа
міцності трохи зростає через те, що при її висиханні зменшується площа січення.
При динамічному навантаженні зусилля на відрив більше, ніж при статичному.
Найбільш слабкими місцями плодоніжки є вузли, обрив качана відбувається біля
його основи.
![]()
*Столон –
підземний пагін, за допомогою якого бульба кріпиться до кореня рослини
Зусилля на розрив зеленого
стебла кукурудзи менше, ніж у зрілого, а межа міцності більша в зрілого.
Для
розриву симподію бавовнику потрібно зусилля, рівне 33...367 Н, причому великі
значення цього зусилля отримані для симподіїв, що мають великі діаметри.
Зусилля відриву симподію від стебла знаходиться в межах 86...204 Н.
Зусилля відриву бульб картоплі від столонів рівне
6,8...19,0 Н, відрив столонів від коренів досягається при зусиллі 9,3...22,0 Н.
Зусилля розриву столонів картоплі рівне 12...19 Н.
Зусилля
розриву пучка пер цибулі складає 73 Н для пучка з зелених листків, 38 Н для
пучка з зів’ялих листів і 28 Н для пучка із сухих, відмерлих листків. Найменше
зусилля потрібно у верхній третині пучка (29…125Н), найбільше – у нижній
третині (44…168Н).
Відділення плодів і ягід від гілок під час збирання можливе разом з
плодоніжками, але можливе і таке відділення, коли плоди і ягоди відокремлюються
від плодоніжок, які залишаються прикріпленими до гілок дерев. При дослідженні
цього явища визначається сила, яка необхідна для відділення плодів і ягід від
гілок. Такими дослідженнями встановлено, що сила опору відриву яблук становить
6,0-36,0 Н, слив - 2,2-11,4 Н, вишень - 0,4-5,0 Н, черешень -
0,5-6,8 Н. Сила опору відриву ягід чорної смородини становить 0,6-1,5 Н,
ягід малини - 1,8-6,0 Н, ягід суниць - 0,8-2,2 Н, ягід аронії
чорноплідної (обліпихи) - 1,0-1,4 Н.
Зусилля відриву і поздовжнього розриву обгорткових листків, які покривають
качан кукурудзи, знаходиться в межах 0,07-0,18 кН. Плодоніжка качана
кукурудзи відривається від основи при зусиллі 0,3-0,8 кН (при діаметрі
ніжки до 18 мм) і 0,7-1,1 кН (при діаметрі ніжки більше 18 мм).
Зусилля відриву пучка гички від столового буряка знаходиться в межах
55-520 Н, а від моркви - в межах 30-520 Н. Відрив пучка листків від
редьки здійснюється при зусиллі 13,3-78,5 Н. Для відриву пучка гички від
кореня кормового буряка потрібне зусилля в межах 200-500 Н. Зусилля
відриву корзинки від стебла соняшника знаходиться в межах 0,25-0,30 кН при
повній стиглості зерна і 0,60-0,65 кН при восковій стиглості.
Під час відриву помідора від плодоніжки остання ніколи не розривається,
розділення відбувається в місці зчленування плодоніжки з помідором. Зусилля,
яке необхідне для відриву стиглого плоду, знаходиться в межах 0,5-20 Н, а
для відриву зелених плодів (помідора) необхідна сила, що рівна 0,5-21 Н.
Для дрібних плодів ця сила менша, ніж для великих.
Зусилля відриву плодів перцю знаходиться в межах 15-120 Н (в
зчленуванні плода з плодоніжкою) і 5-90 Н (на середині плодоніжки).
Зусилля, необхідне для розриву стебла кавунів у нижній його третині,
становить 69-254 Н, в середині 57-215 Н, при вершині 34-196 Н, у гілки першого
порядку 28-106 Н. Для відриву плодоніжки від стебла кавуна потрібне зусилля
2-83 Н.
Зусилля, необхідне для відриву коробочки від сімподія бавовника,
знаходиться в межах 52-113 Н; це зусилля тим більше, чим більший діаметр
сімподія. Для відриву насіннєвої коробочки льону від стебла необхідне зусилля,
яке знаходиться в межах 2-4 Н.
Властивості
рослин залежать від виду і кількості внесених добрив при обробленні і густоти
стеблостою. Так внесення кальцію дозволило підвищити динамічну міцність стебел
кормових бобів.
З
формул (3.1) і (3.2) випливає, що ![]() . З цієї рівності визначається абсолютне видовження стебла Dl, якщо
відомі величини Р, l,
. З цієї рівності визначається абсолютне видовження стебла Dl, якщо
відомі величини Р, l, ![]() і Е:
і Е:
![]() (3.3)
(3.3)
або
![]() , (3.4)
, (3.4)
де ![]() – площа поперечного перерізу стебла.
– площа поперечного перерізу стебла.
За
наведеною формулою (3.4) можна визначити видовження стебел при впливі на них
механізмів машин.
При висмикуванні
бральними апаратами з ґрунту стебла розтягуються і сила Р розтягу кожного з них
повинна бути достатньою для витягування стебла з ґрунту і менше сили, при якій
стебло розривається. Розрахунки за формулою (3.4) з метою визначення видовження
стебла ![]() за умови, що
за умови, що ![]() - довжина стебла від
землі до місця його затиснення в бральному апараті, показали, що при:
- довжина стебла від
землі до місця його затиснення в бральному апараті, показали, що при: ![]()
![]()
Якщо ж ![]() зменшиться до
зменшиться до ![]() , а
, а ![]() збільшиться до 0,4 м, то:
збільшиться до 0,4 м, то:
![]() .
.
Таке витягування
(висмикування) стебел має місце при збиранні льону, картоплі і ряду інших
культур, а також при витяганні з ґрунту підкопаних саджанців плодовоягідних
культур.
При
дослідженні операції висмикування стебел з грунту встановлено, що спочатку
стебло випрямляється і натягується, а потім при подальшому витягуванні стебла
настає обрив бокових корінців, після чого відривається головний корінь (цьому
моменту відповідає максимальне зусилля висмикування); а тоді відриваються
дрібні корінці, які залишилися. Під час групового висмикування (брання) стебел
зусилля висмикування, що припадає на одне стебло, зменшується на 20-40 %
порівняно з бранням окремих стебел. Чим більший діаметр стебла, тим більше
зусилля потрібне для його витягування з ґрунту.
Встановлені
дослідним шляхом основні види залежності між силою, що необхідна для
витягування стебел з ґрунту, і довжиною шляху дії цієї сили подані на
рис. 3.5. З цих графіків видно, що особливої закономірності в даному
процесі немає. У деяких випадках (криві 1, 2, 3) сила брання швидко зростає до
максимуму, в інших випадках (криві 4, 5, 6, 7, 8) сила висмикування росте
повільно, досягаючи максимуму в кінці витягування стебла. Площа, що є під
кривою - це в певному масштабі робота, що потрібна для висмикування стебла з ґрунту.
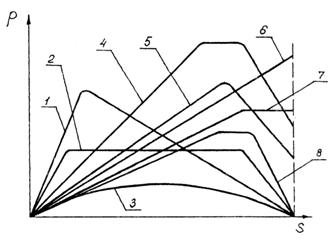
Рис. 3.5.
Основні види залежностей між силою р
висмикування рослин з ґрунту і довжиною шляху дії цієї сили s (пояснення в тексті)
Сила, необхідна для висмикування з ґрунту
стебла льону-довгунця, набуває значення 4 -
12 Н, бадилля картоплі 40 - 160Н, підкопаного коренеплоду буряка
150-290 Н, непідкопаного коренеплоду буряка 430-490 Н, підкопаного
саджанця малини 100-500 Н, непідкопаного саджанця малини 300-1400 Н,
непідкопаного саджанця смородини 115-640 Н, редьки 4-61 Н, цибулі 20-40 Н,
зеленого горошку 30-40 Н, квасолі 40-60 Н, озимого жита 30-80 Н, сої 60-80 Н,
льону олійного 10-110 Н, буряка столового 70-100 Н, моркви 70-110 Н,
буряків кормових 20-160 Н, баклажанів 90-240 Н, помідорів 180-200 Н,
коноплі 210-250 Н, перцю 300-600 Н, кавунів 300-400 Н, кенафу 340-540
Н, капусти 100-950 Н, соняшників 370-500 Н, джута 470-600 Н, бавовнику 230-710
Н, кукурудзи 700-800 Н, клещевини 700-900Н. Робота, що затрачається на
висмикування стебла льону-довгунця з ґрунту, рівна 0,10-0,25 Дж, робота
видалення підкопаного коренеплоду буряка рівна 15-16 Дж. Довжина, на яку
потрібно витягнути стебло льону-довгунця з ґрунту до повного видалення (довжина
шляху дії сили висмикування), набуває значення 2 - 6 см.
Сила,
необхідна для висмикування з ґрунту стебла льону-довгунця, зростає з ростом
числа насіннєвих коробочок на стеблі. На суглинистих ґрунтах ця сила більша,
ніж на супіщаних.
Розглянемо
ще реологічні властивості стебел при розтягу, а
саме – релаксацію і повзучість. Як уже вказувалося, релаксацією називається
процес поступового переходу пружної деформації тіла в пластичну (необоротну),
при якому має місце падіння напружень у матеріалі без зміни деформацій.
Повзучістю називається властивість матеріалу продовжувати деформуватися при дії
на нього навантаження, яке може бути постійним або збільшуватися. Раніше (п.
2.3) зазначалося, що явища релаксації і повзучості при деформації рослинних
матеріалів досить складні і для встановлення закономірностей, що мають при
цьому місце, проводяться експерименти з наступним аналізом і узагальненням
їхніх результатів.
Для
дослідження повзучості, під час дослідів, коли на стебла протягом тривалого
часу діє постійне навантаження, періодично замірюється їхнє видовження. Для
дослідження релаксації, стебла після розтягу залишають у такому стані (без
зміни деформації) тривалий час, поки напруження не падають до деякої постійної
величини, причому під час дослідів періодично реєструється сила розтягу стебла.
Розділивши силу на площу поперечного переріза стебла в середній його частині,
знаходять напруження.
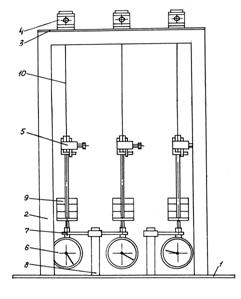
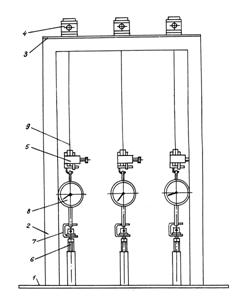
Дослідження
явища повзучості при розтягу рослини проводиться на приладі (рис. 3.6), що
містить такі основні частини: основа 1, стійки 2 (їх чотири), пластину 3,
верхні затискач 4 (їх три), нижні затискач 5 (їх три), індикатори 6 (їх три),
тримачі індикатора годинникового типу 7 (їх три), кронштейни 8 (їх два). Прилад
розрахований на дослідження відразу трьох різних зразків рослин.
Досліджуваний зразок рослини закріплюється
верхньою частиною в затискачі 4. До нижнього кінця рослини приєднується
затискач 5 з вантажем 9. Під дією сили ваги вантажу 9 рослина деформується і
деформація зразка фіксується індикатором 6.
.
|
|
Рис. 3.6. Прилад для дослідження повзучості при розтягу рослини: 1 –
основа; 2 – стійки; 3 – пластина; 4 – верхній затискач; 5 – нижній затискач;
6 – індикатор; 7 – тримач; 8 – кронштейн; 9 – вантаж; 10 – стебло |
Прилад для дослідження релаксації напружень у
навантажених рослинах (рис. 3.7) складається з основи 1, двох стійок 2,
пластини 3, нерухомих 4 і рухливих 5 затискачів, гвинта 6, скоб 7 і
динамометрів 8. Під час проведення досліду випробуваний зразок рослини 9
затискається в затискачах 4 і 5. Обертаючи гвинт 6, натягають через динамометр
8 рослину. Зусилля натягу фіксується динамометром
Релаксація напружень буде мати місце, якщо
натягнути стебло і залишити його на тривалий час у такому стані. Для визначення
напружень необхідно через визначений проміжок часу (наприклад, через секунду,
хвилину, годину) фіксувати покази динамометра, а потім, знаючи параметри січення
стебла, обчислити напруження.
Дослідження
релаксації напружень може проводитися також на екстензометрі при деформаціях
розтягу, стиску і зсуву.
Результати дослідження дослідним
методом реологічних властивостей
стебел при розтягу стебел пшениці представлені графічно
на рис. 3.8, з них на рис. 3.8, а
представлені криві релаксації напружень, а на рис. 3.8, б – криві повзучості. На цих кривих ділянки АВ і А1В1 отримані для вологих
стебел у процесі їхнього природного
висихання. З рис. 3.8, а
видно, що релаксація напружень відбувається
однаково як у вологого, так і в сухого стебла, а через 60…100 годин
напруження стабілізуються. У вологих стебел стабілізація напружень відбувається
трохи пізніше, ніж у сухих.
|
|
Рис. 3.7. Прилад для дослідження релаксації напружень у рослинах при
розтягу: 1 – основа; 2 – стійки; 3 – пластина; 4 – верхній затискач; 5 –
нижній затискач; 6 – гвинт; 7 – скоба; 8 – динамометр; 9 – стебло |
Явище
повзучості (див. рис. 3.8, б) має
місце і в сухих стебел (крива 2), і у вологих стебел (крива 1). У вологих
стебел воно починає виявлятися лише після їх висихання. Починається це на
графіку в точці В1 і
зростає по В1С, але вона (повзучість), мабуть, мала
місце і при висиханні стебел (на ділянці А1В1), проте їхнє видовження,
що повинне було б мати місце внаслідок повзучості, компенсувалося їх
укороченням під час висихання, тобто деформація стебла на цій ділянці не
мінялася і пряма А1В1 (рис. 3.8, б) виявилася паралельно осі абсцис.
Після зняття навантаження відбулося скорочення (часткове відновлення довжини)
стебел по вертикальних прямих СD і C1D1.
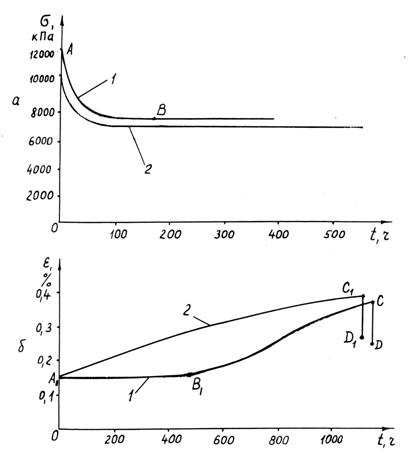
Рис. 3.8. Закономірності
релаксації напружень (а) і повзучості
при σ=4 МПа (б) у стебел пшениці
діаметром 2 мм при розтягу: 1 – стебла вологістю 28%; 2 – стебла вологістю –
16%; АВ і А1В1 –
ділянки, що відповідають висиханню стебел; СD
і С1D1 – вкорочення стебел при знятті навантаження
Якби
скорочення стебла під час сушіння не було рівним його видовженню внаслідок
повзучості, то лінія АВ на рис. 3.8, б виявилась би під кутом до осі абсцис і
трохи наблизилася б за своєю формою до кривої А1С1.
Такі особливості повзучості, коли стебло висихає протягом тривалого проміжку
часу (близько 500 годин), а дослід проводиться протягом ще більш тривалого
проміжку часу (порядку 1100…1150 годин). Якщо ж проведення досліду триває менше
8 годин, що характерно для кривих I-ої стадії повзучості (див. рис. 2.16), то
стебло в природних умовах не встигає
висохнути, і крива повзучості по довжині значно менша відстані АВ.
Більш
повний аналіз дослідних даних з релаксації і повзучості наводиться нижче.
Аналіз дослідних кривих релаксацій напружень при розтягу
одиничних матеріалів показує, що при невеликих коливаннях вологості матеріалу
під час дослідів усі криві однотипні, а саме, у всіх кривих напруження падають
з ростом часу t; це падіння
напруження відбувається плавно і має місце від початку релаксації (при t=0) до деякого значення часу tк, після якого напруження
стабілізуються і вже не змінюються. Графік, що ілюструє сказане, представлений
на рис. 3.9, а. Він містить
криволінійну частину О0ВК
і прямолінійну частину КК1,
паралельну осі абсцис. На графіку по осі абсцис відкладається час t, а по осі ординат – напруження s. Опишемо криволінійну частину графіка математично.
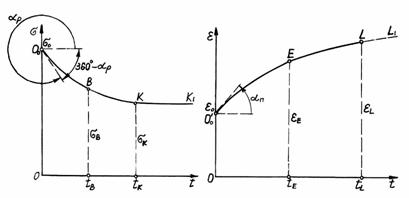
а б
Рис. 3.9. Криві релаксації
напружень (а) і І стадії повзучості (б) при розтягу рослин, побудовані з
метою їхньої апроксимації
Позначимо через s0 напруження s у точці О0,
тобто при t=0, а через sк напруження в точці К кривої,
тобто при t=tк. Позначимо
точку на кривій падіння напружень при t=0,5tк
через В; тоді напруження, що
відповідає цій точці, буде sВ, а час буде tВ,
рівний 0,5 tк.
Криву ОВК опишемо рівнянням:
![]() , (а)
, (а)
де a1 і b1 – постійні коефіцієнти,
обумовлені для кожного матеріалу за результатами дослідів.
Якщо підставити в рівняння наведені вище
значення часу і напруження, то одержимо два рівняння з двома невідомими: a1 і b1. Ці два рівняння мають вигляд:
![]() ;
; ![]() .
.
Розв’язавши їх, знаходимо такі
вирази для визначення коефіцієнтів a1 і b1:
 (3.5)
(3.5)
З урахуванням представлених рівностей
рівняння (а) набуде вигляду:
![]() . (3.6)
. (3.6)
Таке рівняння кривої релаксації напружень у рослинних матеріалах, причому
параметри s0, sК, sВ і tк
визначаються за результатами дослідів; також за результатами дослідів,
скориставшись формулами (3.5),
визначають параметри a1
і b1.
Диференціюванням залежності (3.6) за
часом t знаходять швидкість падіння
напружень при їхній релаксації ![]() :
:
![]() . (3.7)
. (3.7)
Початкова швидкість падіння напружень
при релаксації ![]() знаходиться з (3.7) при
t=0:
знаходиться з (3.7) при
t=0:
![]() .
(3.8)
.
(3.8)
З
порівняння рівностей (3.5) і (3.8) видно, що ![]() .
.
У
чисельнику правої частини рівності (3.8) ![]() ; це значить, що
; це значить, що ![]() являє собою негативну
величину. Як відомо, похідна є тангенсом кута між віссю абсцис і дотичної до
кривої в якій-небудь точці, наприклад, у точці О0 (рис. 3.9, а),
який відрахований від позитивного напрямку осі абсцис проти часової стрілки.
Цей кут на рис. 3.9 позначений aр, він знаходиться в межах від
2700 до 3600, тангенс цього кута негативний. Абсолютна
величина швидкості
являє собою негативну
величину. Як відомо, похідна є тангенсом кута між віссю абсцис і дотичної до
кривої в якій-небудь точці, наприклад, у точці О0 (рис. 3.9, а),
який відрахований від позитивного напрямку осі абсцис проти часової стрілки.
Цей кут на рис. 3.9 позначений aр, він знаходиться в межах від
2700 до 3600, тангенс цього кута негативний. Абсолютна
величина швидкості ![]() рівна з урахуванням
масштабних коефіцієнтів осей графіка тангенса кута 3600–aр на рис. 3.9, а. Чим більший цей
кут, тобто швидкість
рівна з урахуванням
масштабних коефіцієнтів осей графіка тангенса кута 3600–aр на рис. 3.9, а. Чим більший цей
кут, тобто швидкість ![]() по абсолютній
величині, тим сильніше падають напруження.
по абсолютній
величині, тим сильніше падають напруження.
Рівняння
прямолінійної частини КК1
графіка на
рис. 3.8, а, паралельній осі абсцис, буде:
![]() . (3.9)
. (3.9)
Рівність
справедлива при t ³ tк.
Час tк являє собою час падіння
напружень або час релаксації. Крім цього показника і швидкості ![]() , оцінити релаксуючі властивості матеріалу можна шляхом
визначення ступеня зменшення напружень за весь період tк релаксації. Цей показник cр дорівнює:
, оцінити релаксуючі властивості матеріалу можна шляхом
визначення ступеня зменшення напружень за весь період tк релаксації. Цей показник cр дорівнює:
![]() . (3.10)
. (3.10)
Аналіз
дослідних кривих першої стадії повзучості (про цю стадію згадується на с.76...77)
показує, що при невеликих коливаннях вологості матеріалу під час дослідів
зазначені криві, отримані після миттєвої деформації, що виникла відразу після
прикладення навантаження, однотипні, на кожній кривій деформація росте плавно
при збільшенні часу t, що значною
мірою відповідає характеру кривої АВ
на рис. 2.16. Графік, що ілюструє сказане, представлений на рис. 3.9, б. На цьому графіку крива 0EL характеризує першу стадію
повзучості, пряма LL1
представляє початок другої стадії повзучості, час t відкладається по осі абсцис, а по осі ординат відкладається
відносна деформація e.
Позначимо
через e0 відносну деформацію стебла в точці ![]() тобто при t=0, а
через eL – відносну деформацію в кінцевій точці L
кривої, тобто при t=tL.
Позначимо точку на кривій зростання деформації при t=0,5× tL через Е, тоді відносна
деформація, що відповідає цій точці, буде eE, а час буде tЕ,
рівний 0,5 tL.
тобто при t=0, а
через eL – відносну деформацію в кінцевій точці L
кривої, тобто при t=tL.
Позначимо точку на кривій зростання деформації при t=0,5× tL через Е, тоді відносна
деформація, що відповідає цій точці, буде eE, а час буде tЕ,
рівний 0,5 tL.
Криву О¢0ЕL можна
описати рівнянням:
![]() , (б)
, (б)
де a2 і b2
– постійні коефіцієнти, обумовлені для кожного матеріалу за результатами
дослідів.
Якщо
підставити в наведене рівняння значення часу і відносної деформації для точок Е та L, то одержимо два рівняння з двома невідомими: a2 і b2. Ці два рівняння мають вигляд: ![]() ;
; ![]() . Розв’язавши їх,
знаходимо наступні залежності для визначення коефіцієнтів a2 і b2:
. Розв’язавши їх,
знаходимо наступні залежності для визначення коефіцієнтів a2 і b2:
 (3.11)
(3.11)
В
останній рівності 2eЕ > eL + e0, через що b2
є величиною негативною.
З
урахуванням представлених рівностей рівняння (б) набуде вигляду:
![]() . (3.12)
. (3.12)
Таке
рівняння кривої першої стадії повзучості рослинних матеріалів, причому
параметри e0, eL, eЕ і tL
визначаються за результатами дослідів.
Наведені вище параметри a2
і b2 розраховуються за
формулами (3.11) на основі результатів дослідів.
Диференціюванням
залежності (3.12) знаходиться швидкість ![]() росту деформації
матеріалу при першій стадії повзучості:
росту деформації
матеріалу при першій стадії повзучості:
![]() . (3.13)
. (3.13)
Початкова
швидкість росту деформації матеріалу при повзучості ![]() знаходиться з ( 3.13)
при t=0:
знаходиться з ( 3.13)
при t=0:
![]() . (3.14)
. (3.14)
З
порівняння рівностей (3.11) і (3.14) видно, що ![]() =а2.
=а2.
Величина ![]() позитивна. Це тангенс
кута між віссю абсцис і дотичною до кривої повзучості в точці
позитивна. Це тангенс
кута між віссю абсцис і дотичною до кривої повзучості в точці ![]() , відлічуваного від позитивного напрямку осі абсцис проти
годинникової стрілки. Цей кут на рис. 3.9, б
позначений aп, він гострий. Чим більше цей кут, тим інтенсивніше
ростуть деформації.
, відлічуваного від позитивного напрямку осі абсцис проти
годинникової стрілки. Цей кут на рис. 3.9, б
позначений aп, він гострий. Чим більше цей кут, тим інтенсивніше
ростуть деформації.
Час ![]() є часом росту деформації при першій стадії повзучості. Крім
цього показника і швидкості
є часом росту деформації при першій стадії повзучості. Крім
цього показника і швидкості ![]() , при оцінці явища повзучості в першій стадії необхідно знати
ступінь зростання деформації при першій стадії повзучості cп, рівний
, при оцінці явища повзучості в першій стадії необхідно знати
ступінь зростання деформації при першій стадії повзучості cп, рівний
![]() . (3.15)
. (3.15)
За наведеними залежностями оброблені
результати раніше проведених дослідів по розтягу стебел; отримані дані
представлені в табл. 3.2. З таблиці видно, що при релаксації напружень
розтягнутих одиничних матеріалів час tк
був у пшениці і кукурудзи 40…100 год, у соняшника 30 год, у льону 2 години;
швидкість ![]() склала в пшениці, кукурудзи і соняшника (0,6...12,0)×104Па×год-1, у льону – 2×106 Па×год-1, а показник cр рівний в пшениці, кукурудзи і соняшника 1,07...2,05,
у льону він складає 1,04...1,05. Повзучість у першій стадії при розтягу
одиничних матеріалів характеризувалася наступними показниками: час tL у соняшника і кукурудзи
знаходився в межах 2,8...3,5г, у картопляного бадилля і льону він був рівний
0,5...1,0г; швидкість
склала в пшениці, кукурудзи і соняшника (0,6...12,0)×104Па×год-1, у льону – 2×106 Па×год-1, а показник cр рівний в пшениці, кукурудзи і соняшника 1,07...2,05,
у льону він складає 1,04...1,05. Повзучість у першій стадії при розтягу
одиничних матеріалів характеризувалася наступними показниками: час tL у соняшника і кукурудзи
знаходився в межах 2,8...3,5г, у картопляного бадилля і льону він був рівний
0,5...1,0г; швидкість ![]() була в картопляного
бадилля, льону і соняшника в межах 0,001…0,008г-1, а в кукурудзи
вона склала 0,0006…0,0008г-1; показник cп у
картопляного бадилля і льону був у межах 1,15...2,28, у кукурудзи –
1,54...2,34, а в соняшника – 1,17. Такий розкид даних пояснюється складністю будови
матеріалів і залежністю їх міцнісних властивостей від багатьох факторів і,
зокрема, від діаметра стебел. У той же час із наведених даних випливає ряд
закономірностей, а саме: з ростом вологості матеріалу і початкового напруження s0 параметри tк і tL збільшуються, показник cр зростає з
ростом часу tк і вологості
матеріалу, а показник cп зростає з ростом діаметра стебел і зменшенням
початкової деформації e0.
була в картопляного
бадилля, льону і соняшника в межах 0,001…0,008г-1, а в кукурудзи
вона склала 0,0006…0,0008г-1; показник cп у
картопляного бадилля і льону був у межах 1,15...2,28, у кукурудзи –
1,54...2,34, а в соняшника – 1,17. Такий розкид даних пояснюється складністю будови
матеріалів і залежністю їх міцнісних властивостей від багатьох факторів і,
зокрема, від діаметра стебел. У той же час із наведених даних випливає ряд
закономірностей, а саме: з ростом вологості матеріалу і початкового напруження s0 параметри tк і tL збільшуються, показник cр зростає з
ростом часу tк і вологості
матеріалу, а показник cп зростає з ростом діаметра стебел і зменшенням
початкової деформації e0.
Слід зазначити, що криві релаксації і
повзучості, подібні тим, які представлені на рис. 3.9, справедливі значною
мірою для сухих і повітряно-сухих матеріалів. В інших випадках, тобто при
висиханні матеріалів під час релаксації і повзучості, одержувані при цьому
криві можуть містити перегини і ступінчастості, а пряма КК1 (рис. 3.8, а)
може мати невеликий схил у бік осі абсцис.