2.3. Основні закономірності при деформації середовищ

 

Будь-яке стійке розташування частинок у середовищі означає наявність визначеної рівноваги між силами притягання і відштовхування, що може бути порушена і змінена під дією зовнішніх силових полів. Стійке положення частинок має місце при мінімумі потенційної енергії системи.

При проведенні розрахунків з метою визначення положення частинок і деформації середовищ використовуються такі поняття, як сила, тиск, напруження, деформація, тензори напружень і деформацій, складаються рівняння, використовуються такі прийоми, як побудова круга Мора, застосовують закон Гука, залежність видовження тіла від його звуження в поперечному напрямку, враховують реологічні властивості матеріалів, а також деформаційні  властивості сипкого середовища.

Сили. Сила є мірою взаємодії двох тіл. Це може бути взаємодія різних за своєю природою силових полів, що оточують тіла і їхні частинки. Кількісно сили визначають і порівнюють за створеним ефектом (передача прискорення руху тілу або деформація тіла).

Для спрощення розв’язку ряду задач вводять поняття про зосереджені сили, прикладені у деякій точці. Одні сили стосовно розглянутого тіла є зовнішніми, а інші сили – внутрішніми.

Напруження і деформація. Напруження і тиск являють собою силу, що діє на одиницю площі матеріалу. Напруження – це міра інтенсивності внутрішніх сил; напруження виникають усередині матеріалу. Тиск виникає в місці контакту матеріалу з іншим тілом (середовищем).

Деформація – це результат зміни об’єму і форми тіла під дією зовнішніх сил, коли змінюються відстані між частинками тіла і їхнє відносне положення. Деформації можуть бути лінійні і кутові. Результатом лінійних деформацій є зміна об’єму, а результатом кутових деформацій є формозміна.

Напруження може бути позначена буквами σ, τ або іншою буквою, а відносне видовження, що являє собою відношення абсолютного подовження ∆l до початкової довжини l, позначається ε.

Швидкість деформації є першою похідною деформації по часу t, тобто . Пружні деформації в тілах кристалічної будови і рідинах поширюються зі швидкістю звуку в цих тілах; остання дорівнює сотням метрів за секунду. Тому можна вважати, що поширення  пружних деформацій у тілі миттєво наступає за навантаженням.

Тензори напружень і деформацій. Визначення напружено-деформованого стану суцільних середовищ проводиться за допомогою тензорів напружень і деформацій.

Тензорне обчислення – це математична теорія, що узагальнює векторне обчислення і матричну алгебру. У тензорному обчисленні вивчаються тензори, що описуються в кожній системі координат декількома числами. Матриця являє собою прямокутну таблицю якогось числа m´n елементів (чисел, математичних виразів), що складається з m рядків і n стовпців.

Розглянемо більш докладно тензори напружень і деформацій.

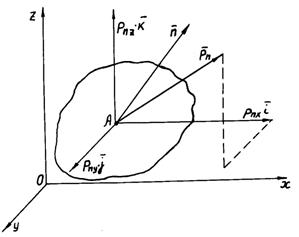
Нехай у якій-небудь точці середовища, наприклад, точці А (рис. 2.1) розглядається деяка площинка, вектор нормалі до якої буде . Нехай далі силова взаємодія двох частин масиву, що лежать по різні сторони від площинки, характеризується в цій точці А вектором напруження , що не обов’язково збігається з вектором .

Рис. 2.1.  Розкладання вектора  на складові

 

Вектор напруження  – це межа, до якої прямує при  відношення тобто  (тут   – сила, а ΔS – площинка, на якій виникає внутрішня сила  і яка перпендикулярна заданому вектору нормалі ). Для різних площинок, що проходять через ту саму точку А, вектори  різні і за модулем, і за напрямком; індекс n вказує площинку, перпендикулярну вектору .

Якщо провести систему координат  x, y, z  з початком у точці О, то вектор  може бути розкладений на три складові, паралельні координатним осям:

 

                             (2.2)

де  – складові (компоненти) вектора; - одиничні вектори вздовж координатних осей  x,  y,  z.

У складових вектора  перший індекс означає нормаль до площинки, по якій виникає вектор напруження, а другий – вісь, вздовж якої спрямований компонент.

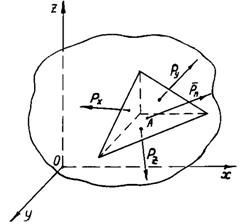
Виділимо в розглянутому середовищі в зоні точки А елементарний тетраедр (рис. 2.2), у якого три грані паралельні площинам  xOy, xOz і yOz, а одна грань похила. Тоді крім вектора напруження , що виникає на похилій грані, на інших гранях унаслідок взаємодії тетраедра з іншим середовищем будуть виникати повні напруження  і  (тут індекси вказують на дію напружень на площинки, перпендикулярні осям  x, y  і  z). Якщо ці повні  напруження розкласти на складові, паралельні координатним осям, то ці складові одержать такі позначення: від  – складові ;  від  –  ; від  –  (тут так само, як у попередньому випадку, перший індекс означає нормаль до розглянутої площинки, а другий – вісь, уздовж якої спрямована складова).

 

Рис. 2.2. Повні напруження на гранях тетраедра, вирізаного в зоні заданої точки суцільного середовища

Складові  і  спрямовані по нормалі до відповідних площинок (граней) тетраедра і являють собою нормальні напруження, що позначимо ,  і . Складові ж  спрямовані по дотичних до відповідних площинок і являють собою дотичні напруження  і  (позначення індексів тут такі ж, як у попередніх випадках).

Нормальне напруження часто приймається позитивним, якщо воно викликає розтяг, і негативним, якщо воно викликає стиск. За позитивний напрямок дотичних напружень приймають позитивні напрямки осей координат, коли розтягуюче нормальне напруження по тій же площинці має напрямок, що збігається з позитивним напрямком осі, паралельно якій діє нормальне напруження. У протилежному випадку за позитивний напрямок дотичних напружень беруться негативні напрямки відповідних осей.

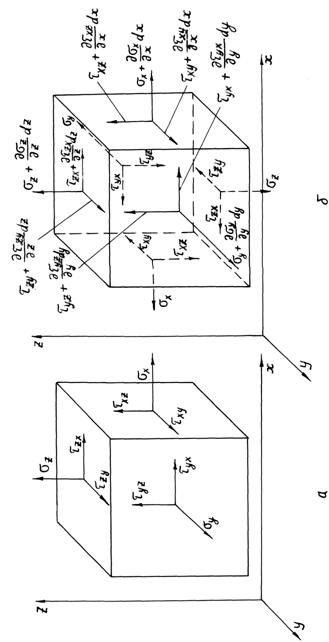
По-іншому це можна сформулювати так. Дотичне напруження позитивне в тому випадку, якщо зовнішня нормаль до площинки збігається за напрямком з координатною віссю, позначеною першим індексом, і діє уздовж позитивного напрямку координатної осі, що вказується другим індексом. Ці напрямки показані на рис. 2.3 а, де показані компоненти напружень по трьох гранях нескінченно малого (елементарного) паралелепіпеда, вирізаного з розглянутого середовища, причому всі напруження позитивні. Усього їх дев’ять компонентів.

Якщо не враховувати внутрішні моменти кількостей руху частинок середовища, то з рівнянь моментів кількості руху нескінченно малого об’єму середовища випливає закон парності дотичних напружень: ; ; . Через це, з дев’яти компонентів залишаються невідомими шість.

 Матриця, у якій напруження розташовані в такий спосіб,

                               (2.3)

називається тензором напружень. У цій матриці перший рядок містить компоненти напружень, що виникають на площинці, яка перпендикулярна осі х, другий рядок – напруження, що виникають на площинці, нормаль до якої паралельна осі y, а третій рядок – напруження, що виникають на площинці, нормаль до якої паралельна осі z.

Рис. 2.3. Компоненти тензора напружень: а – позитивні напрямки компонентів; б – компоненти нормальних і дотичних напружень і їх збільшення

Напружений стан у точці цілком визначений, якщо задано тензор напружень для цієї точки. Матриця (2.3) не зміниться, якщо рядки в ній замінити стовпцями. Через це можна вважати, що в першому рядку матриці розташовані компоненти напружень, паралельні осі х, у другому рядку – паралельні осі y, а в третьому рядку – паралельні осі z.

Як бачимо, величини (2.3) зв’язані із системою координат і при її зміні змінюються самі.

Якщо відомі дев’ять величин матриці (2.3), то кожна з компонент розкладання (2.2) вектора  може бути знайдена за формулами, що виводяться з умови рівноваги тетраедра:

 

        (2.4)

 

Тензор напружень є тензором другого рангу; він визначається дев’ятьма (3²) компонентами. Вектори в тривимірному просторі є тензорами першого рангу і задаються трьома (3¹) компонентами. Скалярні величини (довжина, енергія й ін.) – тензори нульового рангу і мають один (3⁰) компонент.

Вище вказувалося, що величини матриці (2.3) співвіднесені із системою координат і при зміні цієї системи також змінюються. Однак напружений стан у точці середовища не може залежати від довільно вибраної системи координат і повинен володіти незалежними від неї характеристиками, які є інваріантними стосовно неї.

До інваріантних характеристик напруженого стану в точці відносяться, зокрема, головні площинки і головні напруження. Головною називається площинка, для якої повне і нормальне напруження збігається за величиною і напрямком (дотичне напруження відсутнє). Головні площинки і головні напруження можна вказувати для будь-якого тензора напружень. Таких головних площинок три, вони взаємно перпендикулярні і володіють тими властивостями, що діють по них, як уже вказувалося, тільки нормальні напруження, а дотичні відсутні. Ці нормальні напруження і є головними; вони позначаються σ_1,  σ₂ і σ₃ і між ними має місце співвідношення:

,                                   (2.5)

де σ₁ – максимальне напруження, σ₃ – мінімальне напруження, а σ₂ – проміжне за величиною напруження.

Головні напруження визначаються, якщо відомі компоненти тензора напружень (2.3), у будь-якій системі координат х, у, z шляхом розв’язання кубічного рівняння

                           (2.6)

де I_1, I_2, I₃ – перший (лінійний), другий (квадратний) і третій (кубічний) інваріанти тензора напружень, що розраховуються за формулами

(2.7)

В останній формулі в правій частині знаходиться визначник, складений з елементів матриці (2.3).

Унаслідок того, що матриця (2.3) симетрична, кубічне рівняння (2.6) завжди має три дійсних корені σ_1,  σ₂ і σ_3. Крім цих напружень необхідно знати орієнтацію головної площинки, по якій діє головне напруження σ_k (тут k може бути 1, 2 або 3;  так для σ₁    k = 1, для σ₂  k = 2, для σ₃  k = 3). Визначається σ_k шляхом розв’язання системи трьох рівнянь

 

                       (2.8)

 

щодо трьох невідомих

,

які є косинусами кутів нормалі шуканої площинки з напрямками координатних осей х, у, z. Дослідженням цих косинусів установлено, що головні площинки, які відповідають значенням σ_1, σ₂ і σ₃, взаємно перпендикулярні.

Вищесказане відноситься до характеристики напруженого стану тільки в одній довільній точці середовища. У різних точках неоднорідно напруженого середовища тензори напружень (2.3) різні, тому в загальному випадку всі шість компонентів тензора σ_x, σ_y, σ_z, τ_xy, τ_yz, τ_zx є функціями координат x, y, z і часу t.

Вище вказувалося, що в загальному випадку напруження в двох сусідніх точках середовища відрізняються одне від одного. При цьому, якщо виділити в середовищі елементарний паралелепіпед зі сторонами dx, dy і dz, то напруження на паралельних його гранях будуть відрізнятися одне від одного на нескінченно малі величини. Так, якщо на одній грані діють напруження σ_x, τ_xy, τ_xz (рис. 2.3, б), то на паралельній їй грані вже діють напруження  і , де  – приріст функції  на довжині dx; аналогічно  – приріст функції t_xy на довжині dx, а – приріст функції t_xz на довжині dx. Таке ж співвідношення має місце між напруженнями на гранях, перпендикулярних осям y і z.

На рис. 2.3, б показані нормальні і дотичні напруження по всіх трьох взаємноперпендикулярних гранях паралелепіпеда. Передні три грані закривають три інші, котрі прийняті за основні, тому напруження, які діють по гранях, що стоять від основних у позитивному напрямку відповідних осей, мають диференціальні збільшення. Останні використовуються в диференціальних  рівняннях рівноваги  і руху середовища [6, c.80;  25, c.33 і 80].

Якщо на одній із трьох пар граней паралелепіпеда, паралельних одна одній, напруження відсутні (тобто дорівнюють нулю), то вектори напружень, що залишилися, будуть лежати в одній площині, і в цьому випадку буде мати місце плоский напружений стан виділеного паралелепіпеда. Так, стосовно рис. 2.3   то і  Тоді залишаються вектори ,  і  і пояс виниклих напружень буде лежати в серединній площині, паралельній граням, на які не діють напруження. Тензор напружень у цьому випадку являє собою матрицю з двох рядків і двох стовпців: . Аналогічно виходить, коли не діють ніякі напруження на грані, перпендикулярні осям х або z.

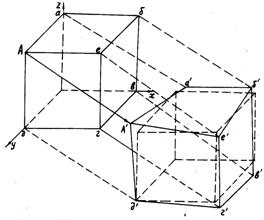
Якщо поблизу точки А (рис. 2.4) у суцільному середовищі виділити нескінченно малий паралелепіпед з ребрами  dx, dy, dz,  то точка А може бути однією з  вершин  такого паралелепіпеда. При дії навантаження паралелепіпед змінить своє положення в просторі і всі його вершини одержать переміщення. Шлях АА' переміщення вершини А  при переході паралелепіпеда в нове положення можна представити як вектор переміщення . Модуль цього вектора дорівнює відстані між точками А і А'. Оскільки різні точки середовища одержують різні переміщення, то вектор  є функцією координат часток у початковому положенні, тобто залежить  також від часу деформації. Вектор  може бути представлений через свої проекції на осі координат:

                                 (2.9)

де  - компоненти вектора . Ці компоненти в загальному випадку є функціями координат часток і часу деформації, тобто

Якщо паралелепіпед абсолютно жорсткий, то нове його положення в просторі може бути отримане шляхом поступального    переміщення    і   повороту.   Але  оскільки   ми

Рис. 2.4. Переміщення і деформація нескінченно малого паралелепіпеда

 

 

розглядаємо елементи деформованого середовища, то при зміні положення паралелепіпеда під дією навантажень можуть змінитися довжини сторін і кути між ребрами, які із прямих стануть тупими або гострими (див. рис. 2.4). При цьому стосовно паралелепіпеда одержимо шість складових деформацій: три лінійних (зміни довжини ребер) і три кутових (зсув). На рис. 2.4 показане початкове положення паралелепіпеда А а б в г д е і його положення А' а' б' в' г' д' е' після переміщення в  просторі  на шлях АА' після деформації. На цьому ж малюнку в  правій частині  крім  паралелепіпеда А' а' б' в' г' д' е', показаний  штриховими  лініями паралелепіпед до деформації.

Відносні видовження ребер позначаються буквою  з індексом, що вказує вісь, паралельно якій отримане кожне видовження (); при цьому відносне видовження вважається позитивною лінійною деформацією, а відносне вкорочення – негативною деформацією. Відносні видовження – це деформації першого роду.

Деформації другого роду – це кутові зсуви або зміна кутів між ребрами, що спочатку були прямими. При цьому позитивному зсуві відповідає зменшення кутів між позитивними напрямками осей, негативному – збільшення цих кутів. Відносні зсуви (кути зсуву) у площині xy або паралельній їй площині позначаються  або , для інших площин (yz, zx) кути зсуву будуть  або  й  або .

Відносні видовження виражаються математично через похідні від компонентів вектора переміщення по координатах. З рис. 2.4 видно, що малий відрізок, паралельний осі х, мав початкову довжину Ае; після деформації його довжина стала А'е', тоді відносне видовження  уздовж осі х  приблизно дорівнює [25, с. 31]:

                               (2.10)

 

де  – компонента вектора переміщення по осі х.

Кутова деформація характеризує відносне зменшення кута між ребрами паралелепіпеда, що спочатку був прямим [25, c. 32]:

.            (2.11)

Відносні видовження уздовж осей у і х і зміна прямих кутів у площинах, паралельних площинам xOz і yOz, виражаються аналогічними формулами.

Можна показати [6, c. 60], що об’ємна деформація  паралелепіпеда внаслідок зміни довжин ребер дорівнює

 

,                                (2.12)

а кути повороту ребер унаслідок деформації зсуву складуть  і .

Розмістимо відносні видовження і зсуви у вигляді матриці, яку побудуємо подібно тензору напружень:

.                         (2.13)

Величини в цій матриці при зміні системи координат перетворяться за такими ж формулами, що й величини в матриці (2.3). Як і в останньої, у матриці (2.13) позадіагональні елементи попарно рівні:  і т.д. Дев’ять величин даної матриці утворюють тензор деформації і називаються його компонентами.

У довільній точці А в деформованому середовищі знаходяться такі три взаємно перпендикулярні площинки, у яких паралельні їм грані нескінченно малого паралелепіпеда і після деформації зберігають прямими свої початкові прямі кути. Змінюються тільки довжини їхніх сторін, що можуть бути коротшими або довшими. Ці три взаємно перпендикулярні напрямки, що утворять ребра даного паралелепіпеда, називаються головними осями тензора деформації, а маючі місце при цьому відносні зміни довжин ребер називаються головними значеннями і позначаються  і .

Якщо координатні осі  направити паралельно головним осям тензора деформації, то позадіагональні компоненти тензора будуть рівні нулю і матриця набуде вигляду

                             (2.14)

Компоненти тензора деформації залежать від координат  і часу .

Окремими випадками напруженого стану середовища є плоскі й одноосьові напружені стани. При плоскому напруженому стані напруження і деформації є функціями тільки двох одних і тих самих координат, наприклад, , . У даному випадку, як бачимо, одне головне напруження дорівнює нулю. У плоскому напруженому стані можуть знаходитися дуже тонкі пластини, у яких напруження на бічних поверхнях відсутні (наприклад, по осі ). Плоскою деформацією вважають також пружно-деформований стан, коли переміщення точок уздовж однієї з координатних осей дорівнює нулю. Частковим випадком плоского напруженого стану можна розглядати лінійний (одноосьовий) напружений стан, коли з трьох головних напружень дві дорівнюють нулю, а переміщення точок середовища відбуваються тільки в одному напрямку (вздовж однієї осі).

Про систему рівнянь механіки середовищ. Універсальними рівняннями механіки для будь-якого середовища є рівняння нерозривності і руху. Рівняння нерозривності виражає закон збереження маси для рухомого об’єму середовища. Рівняння руху є узагальненням другого закону Ньютона і враховує щільність (масу одиниці об’єму) суцільного середовища, прискорення і суму поверхневих і об'ємних сил, що діють на одиницю об’єму середовища. Висновок цих рівнянь приводиться в літературі [25,  c.33].

Круг Мора. Зручним прийомом представлення напруженого стану в точці є графічний метод, запропонований О. Мором; круг, що отримується при цьому, називається кругом напружень, або кругом Мора.

Виділимо в масиві суцільного середовища трикутну призму і розглянемо її плоский напружений стан (рис. 2.5, а).

 

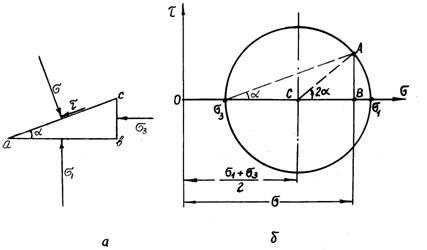
Рис. 2.5. До побудови круга Мора: а) трикутна призма; б) круг Мора

По двох  гранях ab і bc, що є головними, діють головні напруження  і , на третю грань ac, відхилену від грані ab на кут  проти годинникової стрілки, діє нормальне напруження  і дотичне напруження . Дотичні напруження на грані ab і bc відсутні, а діючі на них повне і нормальне напруження збігаються за значенням і напрямком. Якщо розглянути рівновагу призми і зробити необхідні розрахунки, то можна встановити, що для її рівноваги  і  повинні бути рівні:

 

;   (2.15)

 

.                             (2.16)

 

Якщо за рівностями (2.15) і (2.16) побудувати в системі координат  графічну залежність, то це буде круг з центром на осі  на відстані  від початку координат і радіусом (рис. 2.5, б). Це і є круг Мора.

Розташування кола на графіку залежить від прийнятого правила знаків, тобто від вибору позитивних напрямків нормального і дотичного напружень. Будемо для даної побудови вважати, що стискаюче нормальне напруження позитивне, а те, що розтягує, – негативне. Трикутник abc зручно будувати так, щоб грань ab була паралельна осі , тоді кут  буде в лівому куті трикутника і виявиться рівним куту  на колі напружень. Кут  – це кут між зовнішньою нормаллю до грані ac і лінією дії вектора найбільшого головного напруження. Приймемо дотичне напруження по грані ac призми позитивним, якщо вектор, що його зображує, прагне обертати призму відносно її центра ваги проти годинникової стрілки; у протилежному випадку дотичне напруження негативне. Кут  позитивний, якщо грань ab призми, по якій діє напруження , для сполучення з гранню ac, по  якій діє напруження , повертається

на цей кут проти годинникової стрілки. На самому кругу напружень кут  відкладається від осі  проти годинникової стрілки, але у випадку коли , тобто , на крузі напружень краще відкласти негативне значення кута, рівне ; відкладається цей кут від осі  по годинниковій стрілці (тобто вниз), у цьому випадку грань ac трикутника виявляється нижче грані ab.

Таким чином, круг Мора являє собою графічну залежність дотичного напруження від нормального. Кожній похилій грані відповідає визначена точка на колі графіка. Так, грані ac, відхиленій від грані ab на кут , відповідає точка А на колі, радіус якої СА відхилений від осі  на кут  проти годинникової стрілки. Дійсно, для точки А

 

а , що відповідає (2.16). При , а , при   , а .

Дана діаграма побудована для плоского напруженого стану. Нижче буде побудований круг Мора і для просторового напруженого стану.

Закон Гука. Якщо стиснути сталеву пружину, наприклад, рукою, і потім забрати руку, то пружина відновить свою початкову форму. Така відновлювана сама по собі завдяки внутрішнім силам пружності деформація (оборотна деформація) називається пружною. Для більшості пружних тіл при простому їхньому розтягуванні або стиску експериментально встановлена лінійна залежність напружень від деформації. Закон, що виражає цю залежність, називається законом Гука; відповідно до нього середнє значення  по поперечному перерізі центрально стиснутого або розтягнутого тіла залежить від поздовжньої деформації  таким чином:

                                         (2.17)

де Е – модуль пружності (вимірюється в Па).

У випадку пружного зсуву закон Гука має вигляд:

                                          (2.18)

де G – модуль зсуву (Па);  – відносний зсув.

Якщо має місце об’ємна деформація , то за законом Гука середнє напруження , що викликає цю деформацію, дорівнює:

,                                        (2.19)

 

де  – об'ємний модуль пружності (Па).

Зміна поперечного перерізу тіла при розтягу або стиску. Досліди показують, що видовження тіла в поздовжньому напрямку супроводжується пропорційним його звуженням у поперечному напрямку, а при стиску тіла в поздовжньому напрямку має місце розширення тіла в поперечному  напрямку. Якщо відносне поздовжнє видовження позначити , а відносне поперечне звуження (скорочення) , то між ними має місце залежність

,                                   (2.20)

де  – коефіцієнт  пропорційності (безрозмірна величина), названий коефіцієнтом Пуассона. Для металів він знаходиться в межах 0,25...0,35. Для реальних матеріалів, що існують в природі, .

Реологічні властивості матеріалів. При навантаженні матеріалів їхня деформація залежить при всіх інших рівних умовах від часу дії навантаження. Закономірності протікання деформації в часі й умови втрати матеріалами міцності вивчаються наукою, що називається реологією. Реологія вивчає наступні явища: релаксацію, повзучість і тривалу міцність. Фундаментальними властивостями матеріалів, що розглядаються в реології, є пружність, пластичність і в'язкість.

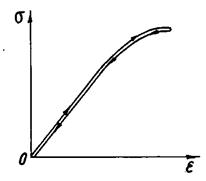
Більшість пружних тіл характеризується залежністю (2.17). Залежність ця прямолінійна і справедлива як при навантаженні (завантаженні), так і при розвантаженні. Графік цієї залежності показаний на рис. 2.6, а. На цьому рисунку лінія розвантаження для наочності умовно трохи відділена від лінії навантаження, насправді ж обидві лінії збігаються. Такі тіла називаються тілами Гука.

 

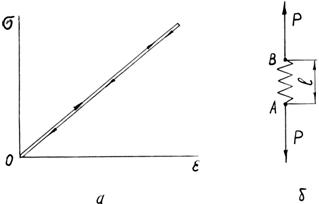
Рис. 2.6. Закономірність деформації ідеально пружного тіла: а – графік залежності  від ; б – механічна модель пружного тіла

 

Властивість пружності умовно зображують механічною моделлю у вигляді пружини (рис. 2.6, б), до кінцевих точок А і В моделі прикладаються зовнішні сили (модель Гука). Робота, затрачена на розтягування пружини, накопичується в ній у вигляді потенційної енергії деформації і потім повністю повертається при знятті навантаження, тобто при зменшенні зовнішніх сил до нуля.

Крім лінійно пружних, є і нелінійно пружні тіла, у яких залежність напруження від деформації не прямолінійна. Графік цієї залежності показаний на рис. 2.7 і на цьому графіку лінія розвантаження умовно відділена від лінії навантаження (як на рис. 2.6, а).

Рис. 2.7. Закономірність деформації нелінійно пружного тіла

Рослинні матеріали не є пружними тілами. Нижче про це буде викладено більш детально.

Розглянемо тепер пластичні тіла. Якщо рукою стиснути тіло, виготовлене з пластиліну, то тіло це розплющиться; після зняття руки з тіла його деформація не відновиться, тіло залишиться розплющеним. Така залишкова або необоротна деформація називається пластичною.

Ідеально пластичне або жорстко пластичне тіло характеризується тим, що на початку завантаження воно не деформується, і лише тоді, коли напруження досягає визначених значень, розвиваються деформації без руйнування матеріалу, причому деформації ці значні і необоротні (остаточні).

Пластична деформація – це залишкова деформація зсуву (ковзання) одних частинок матеріалу щодо інших під дією дотичних сил. Цей зсув найлегше відбувається по поверхнях і напрямках, по яких потрібна витрата мінімальної енергії. Межа пластичності тіла  – це те дотичне напруження, при якому починається пластична деформація. Через це умова настання пластичної деформації показана у вигляді граничного співвідношення:

,                                        (2.21)

де  - дотичне напруження.

Зсув може бути простим переміщенням, коли дотичні сили діють по двох протилежних гранях елементу (рис. 2.8, а), і чистим, коли дотичні напруження виникають по всіх чотирьох гранях виділеного прямокутного елемента при відсутніх нормальних напругах на них. При зсуві обсяг тіла не змінюється, а змінюється лише його форма.

Вище вказувалося, що деформація зсуву оцінюється кутом  зсуву елементів тіла при дії дотичних напружень  (рис. 2.8, а). Тангенс кута  дорівнює , де  – зсув верхнього елемента щодо нижнього, а – висота елементарного шару. Оскільки кут  малий, то . Кут  називають кутом зсуву (кутовою деформацією). Вище про зсув елементів паралелепіпеда говорилося.

 

 

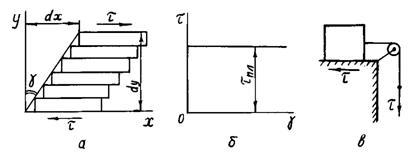
Рис. 2.8. Закономірності  деформації  ідеально  пластичного  тіла: а – простий зсув елементів тіла; б – графік залежності  від ; в – механічна модель ідеально пластичного тіла

 

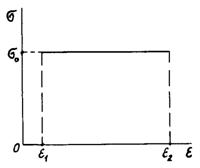
Графік залежності напруження від кута зсуву для ідеально пластичного (жорстко пластичного) тіла показаний на рис. 2.8, б. Лінія зміни напруження ламана. Спочатку (при )   збільшується  від  нуля  до  ,  після  чого  не змінюється.

Властивість пластичності умовно зображують у вигляді механічної моделі поступальної пари, між елементами якої діє постійне тертя (модель Сен-Венана, показана на рис. 2.8, в).

В ідеально пластичного тіла деформація не залежить від швидкості збільшення навантаження, а робота, що витрачається на пластичну деформацію, затрачається на подолання внутрішнього тертя, перетворюється в теплоту і розсіюється, тіло при цьому нагрівається.

Реальне пластичне тіло характеризується графіком залежності напруження від кута зсуву, що відрізняється від графіка на рис. 2.8, б. Справа в тім, що як тільки починається пластична деформація тіла, опір матеріалу трохи падає, у зв’язку з чим зменшується і напруження  до деякого значення, після чого ця напруження залишається постійним. Графічна залежність напруження від пластичної  деформації для  реального тіла показана на рис. 2.9, а. На цьому графіку  – максимальне значення межі пластичності, що має місце на початку (точка А) деформації,  – стале значення межі пластичності, що має місце після закінчення структурних змін у матеріалі (точка В), у результаті чого зменшується від  до . Така зміна напружень має аналогію зі зміною коефіцієнта тертя при русі тіла, коли коефіцієнт цей змінюється від коефіцієнта тертя спокою (початок руху тіла) до коефіцієнта тертя  ковзання (кінець руху тіла).

 

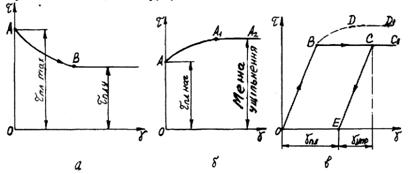
Рис. 2.9. Закономірності деформації реального пластичного тіла (а), пластичного тіла зі зміцненням (б), пружного-пластичного тіла і цього ж тіла зі зміцненням (в)

 

У ряду тіл при пластичній деформації відбувається ріст опору зі збільшенням деформації. Це явище зміцнення, залежність напруження від деформації в цьому випадку має  вигляд, представлений на рис. 2.9, б. На цьому графіку точка А відповідає початку пластичної деформації при напрузі  ,  а  зона А₁А₂ відповідає  межі   зміцнення. Такі тіла називаються   пластичними тілами зі зміцненням.

Якщо з’єднати послідовно моделі Гука і Сен-Венана, то одержимо  модель  тіла, що поводить себе при напругах, менших , як пружне, а при великих – як пластичне. Закономірність деформації такого пружно-пластичного тіла показана на графіку залежності напруження від деформації  (рис. 2.9, в) у вигляді ламаної лінії ОВСС₁, причому на ділянці ОВ тіло деформується як пружне. При зменшенні в точці С напруження розвантаження піде по прямій СЕ. Тоді залишкова деформація  буде пластичною, а деформація  буде являти собою відновлену (оборотну) деформацію завдяки пружності тіла.

Якщо ж у пружно-пластичного тіла для його деформування за точкою В  буде потрібно  збільшити  напругу  по кривій BDD₁, то тіло це являє собою пружно-пластичне тіло зі зміцненням, причому в зоні DD₁ досягнута межа зміцнення.

На відміну від твердих тіл, при навантаженні яких можливі пружні та пластичні деформації, у в’язкого середовища при навантажені має місце деформація у вигляді в’язкої течії, яка починається при нескінченно малих напруженнях зсуву; такими середовищами є рідини. В’язкість – це  здатність рідини чинити опір при дії на неї зовнішніх сил, під дією яких проходять її течія. Ця властивість являє собою прояв внутрішнього тертя в рідинах (рідинне тертя). Швидкість в’язкої течії пропорційна величині напружень.

На рис. 2.10 показаний рух рідини, що знаходиться між двома паралельними пластинами, причому верхня пластина переміщається в напрямку стрілки А. Верхня пластина, що рухається, захоплює за собою рідину, при цьому через в’язкість швидкість руху рідини зменшується зі збільшенням глибини. Так, якщо в деякому шарі швидкість дорівнює , то у розташованому вище шарі буде  тут  - елементарне збільшення швидкості при переході від одного шару до розташованого над ним іншого шару.

Якщо провести систему координат хОу так, як показано на схемі (рис. 2.10), то зміна швидкості  з глибиною z виражається похідною . Ця похідна називається градієнтом швидкості.

Відношення , де  – переміщення верхньої пластини за час , а  – товщина шару рідини, називається градієнтом зсуву .

 

 

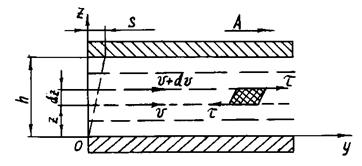
Рис. 2.10. Рух між двома паралельними пластинами рідини, у якої один  шар  переміщається зі швидкістю , а інший – зі швидкістю

 

Закон в’язкості Ньютона виражається в такий спосіб:

,                                   (2.22)

де  – дотичне напруження;  – динамічна в’язкість; – різниця швидкостей сусідніх елементарних шарів рідини; dz – відстань між елементарними шарами; – градієнт швидкості або похідна по часу від градієнта зсуву шарів.

Рівність (2.22) отримана, виходячи з того, що

 

Динамічна в’язкість  або просто в’язкість – це дотичне напруження, необхідне для того, щоб викликати рух шарів один відносно одного зі швидкістю, рівній одиниці; в’язкість має розмірність напруження, помноженого на час. Одиницею в'язкості є паскаль-секунда ( ). Динамічна в’язкість води дорівнює 0,001,  етилового спирту – 0,0012, касторової олії – 1 .

В’язка рідина, для якої справедливе рівняння (2.22), називається реологічним тілом Ньютона і зображується моделлю поршня з отворами, що рухається в заповненому рідиною циліндрі (рис. 2.11, а). У такій конструкції швидкість переміщення поршня пропорційна прикладеній силі Р, з чого випливає, що напруження пропорційне швидкості, що і зображено на рис. 2.11, б.

Робота сил на подолання в’язкості повністю перетворюється в теплоту і є необоротною.

Представлені вище закономірності деформації пружних, пластичних і в’язких тіл використовуються в реології, яка, як уже вказувалося, вивчає такі явища: релаксацію (ослаблення), повзучість і тривалу міцність.

 

 

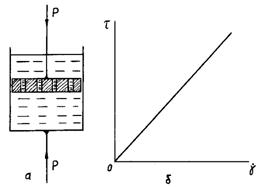
Рис. 2.11. Модель в’язкого тіла (а) і закономірність зміни дотичного напруження при русі рідини (б)

 

Релаксацією напружень називається процес зменшення в часі (розслаблення) діючих напружень при незмінній деформації. Це процес поступового переходу пружної деформації тіла в пластичну (необоротну, тобто залишкову), що відбувається після припинення наростання навантаження на тіло при збереженні його деформації, а усередині  тіла напруження залишаються. Падіння напружень у матеріалі без зміни деформацій пояснюється тим, що в деформованому матеріалі понизилася межа пружності, тобто відбулося його розслаблення.

Процеси, що мають місце при релаксації після припинення зростання навантаження, графічно зображені на рис. 2.12. По осі ординат на рисунку відкладене напруження , по осі абсцис на рис. 2.12, а  відкладений час t, протягом якого має місце зменшення напружень після того, як зростання навантаження припинилося (зростання навантаження припинене при ), а по осі абсцис на рис. 2.12, б  відкладена деформація . Напруження, що діяло в момент припинення зростання навантаження, позначена . Релаксація  напружень на цих графіках характеризується кривою АВ і прямою А₁В₁, деформація  на рис. 2.12, б – це деформація, при якій відбувається релаксація, а штрихова крива ОА₁ на рис. 2.12, б показує, як відбувалося збільшення напруження і  деформації, коли діяло зростаюче навантаження.

 

 

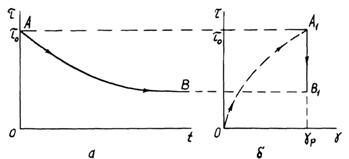
Рис. 2.12. Закономірності при релаксації напружень зі зміною часу (а) і деформації (б)

 

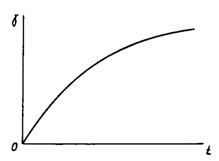
Повзучістю називається властивість матеріалу продовжувати деформуватися при дії на нього навантаження. Графічно це явище при дії постійного навантаження представлене на рис. 2.13, де по осі абсцис відкладена деформація, а по осі ординат – напруження. Графік являє собою пряму, паралельну осі абсцис. Тут  – напруження, при якому матеріал «повзе»,  – деформація матеріалу на початку явища повзучості, а  – деформація наприкінці повзучості.

Рис. 2.13. Закономірність деформації тіла при повзучості

Закономірність, що має місце при повзучості, коли дія навантаження на тіло підсилюється, графічно зображена на рис. 2.14. На цьому графіку показана зміна деформації в залежності від часу дії навантаження. По осі абсцис відкладений час , а по осі ординат – деформація . З графіка видно, що деформація збільшується з ростом часу, що є результатом поєднання в одному тілі властивостей пружності і в’язкості. Прояв цих властивостей у того самого матеріалу залежить від навантаження на нього, його температури, вологості й інших факторів. Підвищення навантаження і вологості приводить до більш сильного прояву рідиноподібних властивостей.

 

Рис. 2.14. Закономірність деформації тіла в часі, коли діюче на тіло навантаження зростає

 

Фундаментальні реологічні властивості в різних матеріалів виявляються по-різному. Пружний початок позначається на оборотності деформацій, в’язкий – на особливості їхнього протікання в часі, пластичний – на появі залишкових необоротних деформацій після того, як напруження досягло деякого визначеного значення. Поєднання цих властивостей позначається на неоднаковому характері відгуку різних матеріалів на миттєві і тривалий час діючі навантаження або на розтягнуті в часі пружні деформації при навантаженні і розвантаженні. У назві тіла першим указують найменування того виду деформації, що викликається відразу ж після прикладання навантаження, наприклад, пружно-пластичне, пружно-в’язке, в’язко-пружне і пружно-в’язко-пластичне тіло.

Для кожного матеріалу існує напруження, що викликає визначену деформацію при нескінченно повільному завантажені. Напруження це найменше з можливих значень і називається межею релаксації. Характер залежності межі релаксації від деформації такий же, як у кривій ОА₁ на рис. 2.12, б. На графіку залежності напруження від деформації це буде найбільше низько розташована крива з можливих кривих зміни напруження.

Зв’язок між явищами релаксації і повзучості в матеріалі можна усвідомити з розгляду графіка, представленого на рис. 2.15. На цьому графіку по осі абсцис відкладена деформація, а по осі ординат – напруження. Штриховою лінією зображена крива зміни межі релаксації   залежно від деформації .

Нехай при збільшенні навантаження зі швидкістю  встановлена залежність 1 напруження від деформації, а при збільшенні навантаження зі швидкістю  отримана залежність 2 напруження від деформації.

Якщо тепер довести деформацію зі швидкістю  до деякого значення  (точка а) і зберегти її далі постійною, то напруження  буде релаксувати до значення , що відповідає кривій деформації зі швидкістю  (точка в), але може релаксувати і до кривої  (точки с).

 

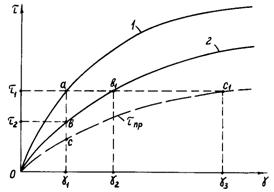
Рис. 2.15. Графік, що встановлює зв’язок між релаксацією і повзучістю: 1 і 2 – криві зміни напруження при швидкостях збільшення навантаження  і ; авс – релаксація; ав₁з₁ – повзучість

 

Якщо ж зберегти постійним напруження , то буде відбуватися деформація внаслідок повзучості. Ця деформація через якийсь час досягне значення  (точка в₁), але може збільшитись і досягти значення  (точка с₁) або ж може відбутись руйнування матеріалу.

Повзучість при деформації тіла може починатися відразу після прикладання навантаження (рис. 2.14) або після миттєвої деформації, що виникла відразу після прикладання навантаження. Останній випадок зображений графічно на рис. 2.16. На цьому графіку миттєва деформація представлена відрізком ОА, але якби повзучість почалася відразу після прикладання навантаження, то відрізок ОА був би рівним нулю і точка А на графіку збіглася б з початком координат О.

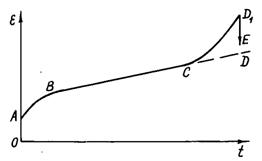
У розвитку повзучості відзначені три стадії, показані на рис. 2.16:

а) перша стадія називається стадією загасаючої повзучості і починається після прикладання навантаження до матеріалу, що може призвести до миттєвої його деформації. У цій стадії повзучість проходить з великою швидкістю (ділянка АВ кривої), яка      однак     поступово    зменшується,    і   явище   повзучості переходить у сталу (другу) стадію, що протікає з постійною швидкістю (ділянка ВС кривої);

Рис. 2.16. Стадії повзучості матеріалу

б) друга – це стадія сталої повзучості; деформація при цьому має, в основному, характер в’язкої течії. Ця стадія може перейти в стадію згасаючої CD або в стадію прискореної CD₁ повзучості; швидкість в’язкої течії може збільшитися, якщо зросте навантаження;

в) третя – це стадія повзучості, що прискорюється, (крива CD₁); у цій стадії деформація розвивається зі зростаючою швидкістю і закінчується або крихким руйнуванням матеріалу (D₁E), або руйнуванням у вигляді течії з високою швидкістю.

Стадія повзучості, що прискорюється, настає при досягненні деякої граничної величини напружень. Якщо ж напруження не досягли цієї межі, то руйнування матеріалу не буде, а повзучість сповільнюється і загасає.

Явища релаксації і повзучості при деформації рослинних матеріалів досить складні. Ця складність пояснюється тим, що властивості матеріалів (вологість і залежні від вологості розміри і щільність) під час дослідів можуть змінюватися, а при зміні властивостей характер протікання релаксації і повзучості також буде змінюватися. Через це для встановлення закономірностей релаксації і повзучості рослинних матеріалів велика  увага приділяється аналізу й узагальненню результатів дослідів [39].

Якщо матеріал піддати деформації при різних навантаженнях, то чим більше діюче навантаження, тим швидше настане стадія повзучості, що прискорюється, і матеріал зруйнується. Зменшуючи навантаження, можна домогтися такого положення, при якому не буде прискореної повзучості, а буде розвиватися тільки згасаюча повзучість, тобто буде забезпечена міцність.

Міцність матеріалу – це його здатність протистояти дії напружень. Тривалою міцністю вважається міцність матеріалу при тривалій дії на нього навантаження. Ця міцність при тривалому навантаженні поступово знижується, але інтенсивність цього зниження різна у різних матеріалів. Мінімальні напруження, при яких відбувається руйнування матеріалу через нескінченно великий проміжок часу, називаються межею тривалої міцності. Міцність вимірюється в одиницях сили або напруження; вона показує, яку силу або напругу і протягом якого часу може витримати матеріал до руйнування.

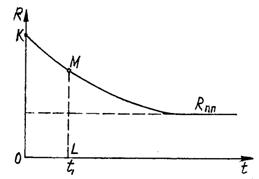
Якщо при прикладанні навантаження матеріал руйнується миттєво, то  це явище  відповідає миттєвій міцності матеріалу при даному напруженому стані. Міцність зв'язана з довговічністю, яка вимірюється в одиницях часу. Графік тривалої міцності являє собою залежність від часу  сили  або напруження, при яких матеріал ще не руйнується. Такий графік, на якому показаний і перехід до межі тривалої міцності, представлений на рис. 2.17. На цьому графіку  ­­- межа тривалої міцності, ОК – миттєва міцність матеріалу, LM – тривала міцність матеріалу при часі t₁.

 

Рис. 2.17. Тривала міцність матеріалу

 

Викладені вище дані використовуються при розгляді складних реологічних тіл, що можуть бути або пружно-пластичними, або пружно-в’язкими, або в’язко-пружними, або пружно-в’язко-пластичними.

Основні властивості і закономірності для сипкого середовища. Сипкі тіла мають особливі властивості, які являються проміжними між властивостями твердих і рідких тіл. Насип із сипких частин може зберегти потрібний обрис лише при наявності стінок, що обгороджують; в той же час у сипких тіл відсутня в’язкість, тобто те, що характерне для рідини. З іншого боку, сипкі частинки, поміщені на похилій площині, рухаються вниз так, начебто це тече рідина.

Сипкими тілами можна вважати зерно, борошно, висівки, дерев’яну тирсу і деякі інші матеріали. Сипке тіло (середовище) має такі властивості:

а) середовище має однакові механічні властивості в різних напрямках;

б) усередині середовища можуть виникати лише напруження стиску  і дотичні напруження зрізу ;

в) ці напруження можуть виникнути одночасно на одній площині усередині середовища і зв’язані залежністю:

,                                     (2.23)

де  - безперервна зростаюча функція від ;

г) частки середовища володіють пружністю і міцністю.

 

Під міцністю розуміють здатність середовища протистояти впливу сил. Сипке середовище вважається міцним, якщо при виникненні нормального і дотичного напружень мають місце лише пружні деформації, а пластичні відсутні.

Пружною деформацією сипкого середовища вважається така виникаюча при прикладанні навантаження деформація, що проходить без порушення рівноваги, тобто без зміни взаємного розташування часток і ковзання між ними, і повністю відновлюється після зняття навантаження. Пластичною деформацією сипкого середовища вважається деформація, що виникає при прикладанні навантаження і проходить при порушенні рівноваги частинок і їхнього взаємного розташування, тобто при наявності ковзання часток одна відносно одної під час збільшення навантаження, при цьому після зняття навантаження початкове взаємне розташування часток не відновлюється.

Залежність (2.23) може бути представлена у вигляді закону пропорційності

 

                                 (2.24)

прямолінійного закону

                                (2.25)

степеневої залежності або більш складної залежності.

У рівностях (2.25) і (2.24)  - кут внутрішнього тертя, а  – початковий опір зсуву (при ), він називається зчепленням. Сипке середовище, для якого справедлива залежність (2.24), називається ідеально сипким середовищем (нев’язко-сипке тіло); середовище, для якого справедлива залежність (2.25), називається зв'язним сипким середовищем.

При спробі зрушити одну частину зв’язного сипкого середовища відносно іншої по прямій  а-а (рис. 2.18, а) відбудеться деформація зсуву, під час якої переборюється опір внаслідок внутрішнього тертя частинок одна відносно іншої і їхнього зчеплення. У зв’язку з цим реологічне тіло,

 

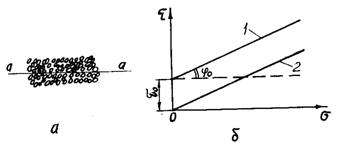
Рис. 2.18. Група сипких часток (а) і діаграма залежності дотичного напруження від нормального (б): 1 – залежність для зв’язного сипкого або погано сипкого середовища; 2 – залежність для ідеально сипкого (незв’язного) середовища.

 

характерне для сипкого середовища (тіло Кулона), зображується у вигляді механічної моделі поступальної пари (так само, як пластичне тіло Сен-Венана, рис. 2.8, в), але з додатковим тиском на повзун і додатковим зчепленням між елементами поступальної пари. Зсув однієї частини частинок відносно іншої відбудеться, коли дотичне напруження  внаслідок дії зовнішньої сили виявиться рівним правій частині рівності (2.25), де , як вже вказувалось, є зчепленням або опором зсуву, що не залежить від нормального тиску (вимірюється в тих же одиницях, що й тиск і напруження).

Якщо ж

                              (2.26)

то зсув не відбудеться.

Величина  дорівнює, де  - коефіцієнт внутрішнього тертя середовища.

Графічна залежність дотичного напруження від нормального тиску за (2.25) представлена на рис. 2.18, б (пряма 1). Це похила пряма, яка починається на висоті  від початку координат. Для ідеально сипкого середовища залежність  від   по (2.24) зображена прямою 2 на цьому ж рис. 2.18, б.

Рівновага сипкого середовища – це такий його стан, при якому відсутнє ковзання часток одна відносно одної.

Сипке середовище знаходиться в рівновазі, якщо задовольняється нерівність (2.23). Графічно це можна показати на діаграмі, де зображені круги напружень. Вище вже був побудований круг напружень для плоского напруженого стану (рис. 2.5, б). Для просторового напруженого стану, коли на три взаємно перпендикулярні площадки діють головні напруження  і , круги напружень будуть мати вигляд, представлений на рис. 2.19. Це сполучені круги напружень 1-2, 1-3, 2-3 для сімейства площин, паралельних головним осям, уздовж яких діють вектори  і . Можна показати, що значення нормального і дотичного напружень  і  для площин у просторі зображуються відповідно абсцисами й ординатами точок заштрихованої на рис. 2.19 області діаграми.

Якщо провести в осях координат криві  [див. нерівність (2.23)], то великі круги напружень будуть лежати або усередині цих кривих (рис. 2.19, а), або в граничному випадку торкатися їх (рис. 2.19, б), але можуть і перетинати ці криві. У випадку, коли великий круг напружень лежить усередині кривих
, то це буде негранична рівновага (стійка рівновага) сипучого середовища, у випадку дотикання великого круга напружень до кривих  буде гранична рівновага сипкого середовища. Перетин кривих  кругами напружень свідчить про порушення рівноваги середовища.

 

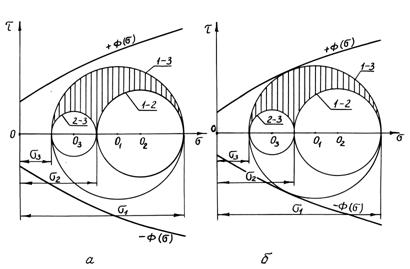
Рис. 2.19. Круги напружень для просторового напруженого стану і схеми рівноваг: а – рівновага негранична; б – рівновага гранична

 

Якщо відомі напруження  і  при граничній рівновазі середовища і круг напружень для даного елементарного обсягу середовища, то по кругу знаходять кут  нахилу грані ас трикутної призми (рис. 2.5), а потім і положення цієї грані призми, по якій відбувається зсув середовища.

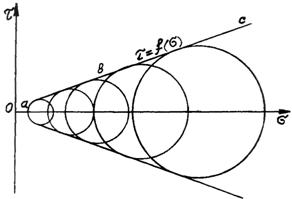
Досліджуючи експериментально напружений стан середовища і його руйнування при різних напруженнях, можна потім побудувати за цими даними круги Мора й одержати сукупність окружностей. Така сукупність представлена на рис. 2.20. Крива, що  огинає їх,  характеризує  граничний стан матеріалу, тобто умови, при яких у середовищі настає руйнування і діють граничні дотичні напруження.

 

Рис. 2.20. Огинаюча крива граничних напружень, при граничній рівновазі середовища

 

Такою огинаючою кривою, на рисунку 2.20 є лінія aвc, близька за формою до прямої. Рівняння цієї  прямої,  якій апроксимується крива, що огинає, виражається залежністю (2.25). Для ідеально сипкого середовища ця пряма проходить через початок координат О під кутом внутрішнього тертя  до осі абсцис (пряма ця показана нижче на рис.2.21 і позначена OD).

 

Рис. 2.21. Зображення діючого і бічного тисків на кругу Мора

 

У випадку, якщо сипке середовище знаходиться в якій-небудь ємкості, для її рівноваги повинні дотримуватися наступні умови:  на вільній поверхні і  на поверхні дотику середовища зі стінками ємності, де  - коефіцієнт тертя середовища об стінки ємкості. При порушенні рівноваги сипке середовище сприймає стан текучості, під час якого відбувається внутрішнє ковзання часток одна відносно одної по елементарних площадках.

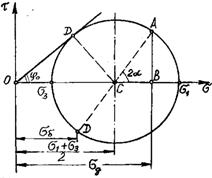
Середовище, що знаходиться в ємкості, тисне на стінки з бічним тиском, яке позначимо . Цей тиск залежить від діючого тиску , а кут між площинами, на які діють  і , складає . Відношення бічного тиску до діючого тиску називається коефіцієнтом бічного тиску (розпору). Якщо цей коефіцієнт позначити , то

                                       (2.27)

 

На крузі напружень (круг Мора) для плоскої задачі точки діючого і бічного тисків знаходяться на протилежних кінцях того самого діаметра (рис. 2.21).

З вищесказаного випливає, що коефіцієнт бічного тиску не є величиною постійною і залежить від кута нахилу площини діючого тиску до площини головного напруження. Коефіцієнт бічного тиску набуває мінімального значення , коли найбільше головне напруження (рис. 2.21) є діючим тиском, а найменше головне напруження  є бічним  тиском, причому сипке середовище знаходиться в граничній рівновазі. Максимальне значення  коефіцієнт бічного тиску одержує, коли найменше напруження  є діючим тиском, а найбільше головне напруження  є бічним тиском, причому середовище знаходиться в граничній рівновазі. Таким чином:

;          .                          (2.28)

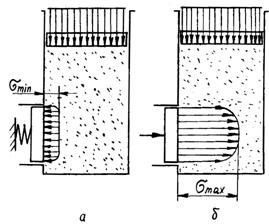
Бічний тиск вважається активним, якщо він менший від діючого тиску, і пасивним, коли він більший від нього. На рис. 2.22 наведені можливі схеми дії сил у таких випадках. Сипке середовище, поміщене в ємкість з бічним поршнем, при активному тиску тисне на бічний поршень вліво із силою , де F – площа поршня; ця сила значно менша від сили , необхідної для переміщення бічного поршня вправо і подолання пасивного бічного опору середовища. Таким чином, сипке середовище, пасивно опираючись заглибленню в нього поршня, тисне на нього з набагато більшою силою, ніж при активному його виштовхуванні.

 

Рис. 2.22. Схеми, що пояснюють активний (а) і пасивний (б) бічні тиски

 

З рисунка 2.21 видно, що

 

             (2.29)

Вище вказувалося, що коефіцієнт бічного тиску залежить від кута нахилу площини діючого тиску до площини головного напруження. Площини діючого тиску і головних напружень показані на рис. 2.23, на якому зображені трикутні призми стиснутого матеріалу з однією загальною стороною bc. На цій схемі площинами діючого і бічного тисків будуть bc і cd, а площинами головних напружень будуть ca і ab. Кут між площинами ab і cb дорівнює куту a, приведеному на рис.2.5, а, а кут між площиною ab і похилою площиною db позначений d.

 

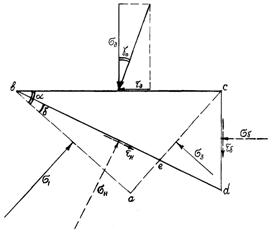
Рис. 2.23. Розташування площин діючих і головних напружень

 

Діючі тиски позначені  (нормальний) і  (дотичний), бічні тиски позначені  (нормальний) і  (дотичний), нормальний і дотичний тиски на похилу площину db з боку призми bае позначені  і . Якщо розглянути при граничній рівновазі явище, представлене на рис. 2.23, і врахувати рівності (2.29), то

  (2.30)

З порівняння схеми  на рис. 2.23 зі схемою на рис. 2.5, а видно, що по лінії bе на рис. 2.23 зображені лише тиски  і  призми baе на призму bеdc; на призму ж baе з боку призми bеdc будуть діяти по лінії bе такі ж за величиною тиски, але протилежно спрямовані (вони не зображені на схемі). Через це, трикутник baе на рис. 2.23 ідентичний трикутнику abc на рис. 2.5, а і тиски  і  за величиною і можна визначити за формулами (2.15) і (2.16), якщо в них замість a підставити кут d.

Для ідеально сипкого середовища співвідношення між мінімальним значенням коефіцієнта бічного тиску  і кутом внутрішнього тертя  можна вивести з розгляду трикутника OCD на рис. 2.21. На цій схемі, як уже вказувалося, пряма OD представляє собою лінію, що огинає, для сукупності окружностей Мора, якби вони були побудовані на рис. 2.21 так, як це зроблено на рис. 2.20. Відхилена пряма OD від осі абсцис на кут . Трикутник ОСD прямокутний, прямим кутом є кут ОDC. Відстань DC дорівнює , а відстань ОС дорівнює . З розгляду трикутника OCD видно, що . Зробивши перетворення, одержимо:  . З цієї рівності знаходимо:

.                                 (2.31)

Така залежність для визначення  для ідеально сипкого середовища. Для зв’язного сипкого середовища в літературі [29, с.77-81] виведені відповідні залежності.

Промноживши чисельник і знаменник дробу в правій частині рівності (2.31) на , одержимо:

.

Використовуючи далі відому тригонометричну формулу половинного кута, остаточно знаходимо:

 

.                                (2.32)

 

Якщо провести осі по катетах ac і ab трикутника abc (див. рис. 2.23), скласти суми проекцій сил на ці осі внаслідок дії напружень ,  ,  і    і прирівняти ці суми до нуля, то одержимо рівняння:

 

 

де ab, ac і bc – довжини сторін ab, ac і bc трикутника abc, а
 - кут  між напруженням  і результуючою напружень  і , . Поділивши одну рівність на іншу, з урахуванням того, що , а , одержимо , звідки . Проводячи подальші перетворення, остаточно одержимо:

 

                              (2.33)

 

 

Дане рівняння встановлює співвідношення між параметрами, що визначають положення головних площин напружень і напрямок діючих сил.