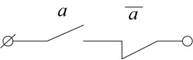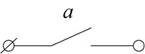Тема 3-4. Алгебра логіки і синтезу  цифрових електронних схем

 

3.1 Основні положення алгебри логіки

Алгебра логіки є математичний апарат, за допомогою якого використовується синтез і аналіз логічних схем. В якості структурного алфавіту вибирають, як правило, алфавіт, що складається з двох елементів. Такий алфавіт називається двійковим, а його букви відповідають числам 0 і 1.

Слід зазначити, що двійковий алфавіт як структурний алфавіт у цифрових машинах, використовується для оцінки внутрішній стан і стан вхідний та вихідний ланцюгів не слід плутати з двійковю системою числення для представлення чисел.

У сучасних цифрових машинах найбільш часто використовуються такі зображення елементарних сигналів, структурного алфавіту бінарних компонентів:

- наявність імпульсу електронного струму і відсутності імпульсу електричного струму;

- високий електричний потенціал і низький електричний потенціал;

- електричний струм великої сили та електричні струми малої сили;

- імпульси позитивної та негативної полярності.

У двійковому структурному алфавіті таких комбінаційних схем визначеними за допомогою функцій, які приймають тільки два значення 0 і 1 [3].

Змінні, які можна взяти тільки двох значень 0 і 1 залежать від змінних, кожна з яких може прийняти тільки два значення 0 і 1.

Змінні, які можна взяти тільки двох значень 0 і 1, називаються двійковими чи логічними змінними.

Змінні можуть бути при трьох основних умовах:

- логічне додавання ;

- логічне множення;

- логічне заперечення (відповідає логічним функцій АБО; І; НЕ).

 

Логічне додавання (диз'юнкція)  позначається символом «+» або (V).

Логічне додавання (кон’юнкція) позначається точкою або символом, & або в буквенному вирази не позначається.

Логічне заперечення (інверсія) позначається рискою над символом елементу.

Функції будь-якої скінченної кількості двійкової змінної, які здатні також приймати два значення 0 і 1, зазвичай, називають перемикальними чи логічними функціями.

Область визначення булевої функції від (n)  змінних служить сукупність з
n-мірних впорядкованої множини (вектори розмірності n ), компонентами яких  є букви двійкового алфавіту 0 і 1. Ці набори вхідних змінних називають кортежами або точками.

Для будь-якого n = 1; 2; 3;... серед n-мірних двійкових наборів можна ввести лексикографічну (природну) впорядкованість, враховуючи будь-який двійковий набір чисел представлення, для деяких невід'ємне ціле число бінарних систем числення.

Наприклад, для n=4, набір 1110 представляє число , а набір 0101 – число .

Число, за яким подано даний набір (розглядається як двійковий код), умовно, називають номером цього набору.

Число змінних, які входять до складу набору, будемо називати розмірністю цього набору. Природний порядок n-мірних наборів (двійкові) ми отримаємо, розміщуючи ці набори за зростанням їх номерів.

Наприклад, n = 3, він буде виглядати наступним чином:

Як ви можете бачити, перший в цьому місці буде нульовий набір (всі компоненти, які дорівнюють нулю), останній – одиничний набір (всі компоненти, де є одиниці).

Двійковий набір повністю визначається його номером та розмірністю. Розмірність набору n нумерується цілими числами від 0 до . При цьому, точно двійковий n-мірних наборів (n = 1; 2; 3.) і має точно різні булевих функції від n  змінних (n = 1; 2; 3;...).

 

Таблиця 3.1 – Таблиця наборів N = 3

Набори	Номер
000	0
011	1
010	2
011	3
100	4
101	5
110	6
111	7

Наприклад, n=3, маємо число наборів  ;  кількість булевих функцій – від n змінні .

Серед булевих функцій від n змінні знайдено функції так званих втрачених і невтрачених функцій .

Невтрачені функції  такі n-змінні функції, які залежать від всіх цих змінних:

                                        (3.1)

 

Втрачені функції є ті, які містять у своєму складі  менш ніж n змінні:

 

 

3.2 Способи встановлення логічних функцій

Існують різні способи встановлення або презентацій логічних функцій. Основні з них включають:

Словесні подання – відображає словесні відносини значень логічних функцій і їх аргументи. Словесні презентації логічних функцій передували будь-якому іншому методу представлення, який відображає неформальні відносини між аргументами і функцією.

Табличний метод – передбачає завдання логічної функції у вигляді таблиці відповідності (таблиці істинності стану). Ця функція презентується у вигляді таблиці, в лівій частині якої  виписують всі можливі набори аргументів за порядком зростання їх номерів від верху до низу , а в правій частині таблиці, для кожного набору встановлюється значення функції. Приклад такого представлення логічних функцій для n = 3 наведений у таблиці 3.2.

Коли накопичення значень будь-яких функцій на n змінні можна розглядати як запис 2ⁿ розрядного двійкового числа. У нашому прикладі y = 01010011. Слід зазначити, що в майбутньому, коли за допомогою поля таблиці істинності номери введення наборів будуть пропущені.

 

Таблиця 3.2 – Таблиця істинності	Таблиця 3.3 – Матрична таблиця істинності
N a b c Y 0 0 0 0 0 1 0 0 1 1 2 0 1 0 0 3 0 1 1 1 4 1 0 0 0 5 1 0 1 0 6 1 1 0 1 7 1 1 1 1	bc  a  00 01 10 11 0 0 1 0 1 1 0 0 1 1

 

Для скорочення табличних записів логічних функцій з великою кількістю змінних () використовується:

Матричні таблиці відповідності. Рівна кількість клітинок у цій таблиці рівна 2ⁿ, а на краях таблиці вліво і зверху відкладають циклічні двійкові файли аргументів, а зверху розміщують аргументи нижчих розрядів, зліва –  вищих розрядів. У клітинці під номером у двійковому коді, який розташований на перетині відповідно рядка і стовпця, вписують одиницю, якщо передбачена функція при цьому наборі вхідними змінними дорівнює 1, або нулю – якщо функція на цей набір приймає нульове значення. Зразок запису функцій трьох змінних (з попереднього прикладу), де вказані двійкове значення одиниць, встановлює 1, 3, 6, 7, що показано в таблиці 3.2.

Аналітичний метод завдання. Аналітичний метод роботи функцій є логічною функції, що задається у вигляді алгебраїчних рівнянь, і в якій змінні  взаємопов'язані між собою  символами логічних операцій.

Існують дві основні форми запису логічних функцій, які в алгебраїчній формі називаються нормальними.

Перша, диз'юнктивна нормальна форма (ДНФ) – являє собою логічну суму елементарних логічних частин або диз'юнкцію елементарних кон’юнкцій, кожна з яких як аргумент або її заперечення входить  не більше одного разу.

Наприклад,

 

.                                        (3.2)

 

Друга – кон'юнктивна нормальна форма (КНФ), логічний продукт елементарних логічних сум (або кон'юнкція елементарних диз'юнкцій).

Наприклад,

 

                      (3.3)

 

Елементарними називають такі диз'юнкції або кон'юнкції, кількість змінних яких менше, ніж загальна кількість змінних, від яких залежить функція. Наприклад, функції (3.2) і (3.3) залежать від трьох змінних і двох з трьох компонентів диз'юнкції і кон'юнкції, відповідно є загальна кількість змінних, так що вони неелементарні [4].

Розглянемо функцію, викладену в таблиці 3. 1, вона дорівнює 1 на наборах змінних з номерами 1, 3, 6, 7, а решта наборів дорівнює нулю. Отже, формулювання запису цієї функції з одноразовим значенням можуть бути представлені наступним чином:

Функція дорівнює одиниці, якщо:

1). а = 0 І в = 0 І с = 1        АБО               2). а = 0 І в = 1 І с = 1;

3). а = 1 І в = 1 І с = 0        АБО               4). а = 1 І в = 1 І с = 1.

 

При заміні логічних операцій АБО і І їх формальних позначень, легко отримати аналітичний запис функцій:

 

                                              (3.4)

 

В порівнянні з (3.2) легко зрозуміти, що функція в рівнянні (3.4), записана в диз’юктивній нормальній формі, але вона складається з кон’юнкцій, які включають в себе повний набір змінних, тобто неелементарних.

Така кон’юнкція, яка включає в себе повний набір змінних, де функція дорівнює 1, називається мінтермом запису функції. Суму мінтерму (тобто диз'юнкцію мінтерму) називають ідеальною диз'юнктивною формою (ІДНФ).

Аналогічно кон’юнкція, яка включає в себе повний набір змінних, на якому функція дорівнює нулю, називається макстермом, і запис функції у вигляді суми макстермів називається ідеальною кон’юнктивною формою (ІДНФ).

Тому функцію (таблиця 2.1) можна записати в такий спосіб:

 

                                             (3.5)

 

Протиріччя, які полягають у тому, що ІКНФ записані в рівняння (3.5) як сума (диз'юнкція) макстермів, легко виключена, якщо зауважити, що в рівняння (3.6) записана не сама функція, а її заперечення. Беручи заперечення від лівої та правої частин рівняння (3.4) після перетворення буде:

 

.                  (3.6)

 

Звідси випливає правило для знаходження в таблиці істинності ІКНФ: щоб знайти ІКНФ логічну функцію, необхідно перемножити суму оберненого аргументу з цих наборів, в якій функція дорівнює нулю.

Таким чином, будь-яка функція логіки з табличної форми може бути перетворена в аналітичну за допомогою елементарних логічних функцій, таких як І, АБО, НІ.

Аналітична форма функцій дає змогу сформулювати основні закони (аксіоми) алгебри логіки, які записуються для операцій І, АБО окремо, і вона буде розглянута нижче.

Числовий метод.

Цей метод запису функції використовується, щоб зменшити його запис, функція написана у вигляді логічної суми десяткових чисел двійкових наборів, на яких функція дорівнює нулю, наприклад, для функції, заданої  у таблиці 3.1

або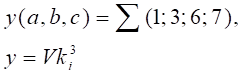

коли (i) = 1, 3, 6, 7,

що читається як: функція трьох змінних дорівнює диз'юнкції мінтермів k, де k_i = 1, 3, 6, 7.

Чисельний метод завдання логічних функцій на додаток до простоти і компактності запису значно спрощує синтез логічних схеми при використанні табличних методів синтезу.

 

3.3 Основні закони формальної логіки

Існують чотири пари основних законів:

- дві переміщувальні;

- дві з’єднувальні;

- дві розподілу;

- дві інверсій.

Переміщувальний закон (закон комунікативності).

Порядок розміщення змінних не впливає на логічну суму.

 

                                           (3.7)

З’єднувальний (Закон асоціативності).

Результати послідовного додавання або множення кількох змінних не залежать від порядку цих дій (тобто в математичних виразах суми і не потрібно писати в дужках):

 

                      (3.8)

 

Розподільний (дистрибутивний закон).

Розподільний закон щодо додавання вказує на те, що загальний множник завжди можна винести за дужки:

 

                                                       (3.9)

 

Цей закон, як і попередні, подібний аналогічному закону звичайної алгебри. Однак розподільний закон відносно множення не містить аналогічного у звичайній алгебрі:

 

                                     (3.10)

 

Закон інверсії (закон заперечення).

Інверсія суми вхідних елементів дорівнює добутку цих змінних:

, а добуток  інверсії вхідних змінних дорівнює сумі інверсій змінних: .

Коли будь-яке число більше двох змінних, то застосовується інший вид закону заперечення – правило де Моргана:

 

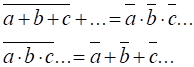                                                (3.11)

3.4 Аксіоми алгебри

1)          1 + 1 = 1;                ;

2).       0 + 0 = 0;                 ;

3).       1 + 0 = 1;                   ;

4).       ;                       (закон константи);

 

3.5 Основні тотожності алгебри логіки

Під час перетворення алгебраїчних логічних функцій законів алгебри логіки широко використовуються наслідки цих законів (які іноді називають додатковими законами або правилами перетворення). Перші п'ять з них є елементарними висловами:

1. Нульова множина (Закон додавання та множення 0):

  

 

2. Універсальна множина  (закон додавання та множення на 1):

 

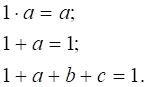
3. (Закон ідентичності). Повторення:

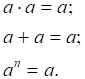
4. Доповнення (Закон протиріччя):

 

5. Подвійна інверсія (Закон подвійного  заперечення):

Крім того, існує складніша логіка конструкції, яка відіграє велику роль у перетворенні структурних формул на основі базових висловлювань:

6. Закон поглинання:

 

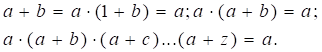
7. Просто склеювання:

 

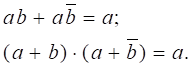
8. Узагальнене склеювання:

 

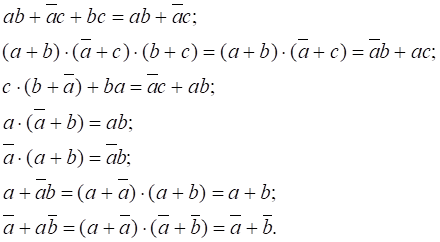
9. Теорема де Моргана:

 

3.6 Функції однієї змінної

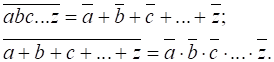
Інтервал зміни аргумента має чотири функції з однією змінною, яка називається нульовою, одиничною, повторення і заперечення (таблиці 3.4 та 3.5).

Нульова  і одинична функції є константами. Функція У₀ називається нульовою, якщо вона дорівнює нулю при будь-якому значенні аргумента а. Аналогічно, У₃ називається одиничною функцією, якщо вона завжди приймає  одиницю при будь-якому значенні аргумента а.

 

Таблиця 3.4 – Таблиця істинності для функції однієї змінної

Аргумент	Функції та їх номери
а	У0	У1	У2	У3
0	0	0	1	1
1	0	1	0	1

 

Таблиця 3.5 – Назва і  позначення функцій однієї змінної

 

Нульова функція може бути цілком постійним відключення навантаження від джерела живлення, а одинична – постійним підключенням навантаження до джерела живлення.

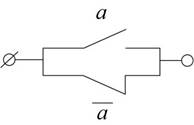
Стосовно схем на контакт елементів одинична функція означає постійно замкнутий ланцюг, а нульова функція є постійно роз’ємним ланцюгом.

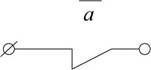
Для звітності а і у будемо називати рівними (ідентичні) і записувати У₁ = а, якщо вони одночасно істинні (1), і одночасно неправдиві (0). Елемент, який реалізує цю функцію, називається повторювальним, а y – називається запереченням (або інверсією) виказуванням а і записується: , якщо у – істина, коли а – хибне і у – хибне, коли а – істина. Логічний елемент носить назву інвертор або елемент, НІ.

 

3.7 Функції двох змінних

Функції двох змінних так само як функції однієї змінної є основними функціями алгебри логіки, тому що ці функції можуть бути узагальненими функціями будь-якого числа із змінних.

Як у випадку з функції однієї змінної, функції двох змінних на відповідному наборі можуть приймати значення: нульової одиничної, повторення і заперечення.

Тобто, на додаток до змінних, мають місце логічні конструкції, характерні тільки для випадку змінні. До них належать: диз'юнкція, кон’юнкція, імплікація, еквівалентність, заперечення  кон’юнкції,  заперечення диз'юнкція, і заборона (таблиця 3.6).

 

Таблиця 3.6 – Таблиці істинності для функцій двох змінних

Аргументи		Логічні функцій і їх номери
а	в	У0	У1	У2	У3	У4	У5	У6	У7	У8	У9	У10	У11	У12	У13	У14	У15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

 

3.8 Базисні логічні функції

Будь-яка логічна функція може бути представлена сукупністю елементарних логічних функцій: диз'юнкція, кон’юнкція, або їх суперпозиції інверсії. Набір елементарних функцій АБО, І, НІ  називають функціонально завершеними або базисним (базисом). Крім того, існують два базиса:І-НІ; АБО-НІ.

 

3.9 Принцип двійкової булевої алгебри

Якщо у виразі кон'юнкцію замінити на диз'юнкцію і проінвертувати двох змінних, то виявиться попереднє значення інверсії функції . Аналогічним чином, якщо вираз диз'юнкцію замінити на  кон'юнкцію і проінвертувати обох змінних, виявиться інверсія попереднього значення функції .

Вказані властивості логічних функцій відображають принцип двоїстість булевої алгебри.

 

3.10 Ідеальна диз'юнктивна нормальна форма (ІДНФ) написання  булевих виразів

ІДНФ є одним з аналітичних форм представлення перемикальних  функцій. Булеві вирази простих логічних функцій можуть бути записані на їх словесних описах. Щоб отримати аналітичні форми (бульевих виразів), рекомендується використання таблиці істинності.

Припустимо, що логічну функцію трьох змінних налаштовано в таблиці істинності (таблиця 3.7).

 

Таблиця 3.7 – Таблиця істинності

№ набору	С	В	А	F
0	0	0	0	0
1	0	0	1	1
2	0	1	0	0
3	0	1	1	0
4	1	0	0	1
5	1	0	1	1
6	1	1	0	1
7	1	1	1	0

Ця функція має чотири конституанти, одиниці К1, К4, K5 і K6 (конституанта одиницею) є одиничне значення ПФ за один конкретний набір. Для перемикальних функцій трьох змінних може бути вісім конституант одиниць. Якщо функція приймає одиничне значення на всіх наборах, то конституанта одиниць записав у вигляді кон’юнкції.

 

 

У нашому прикладі:

 

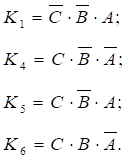
Логічний вираз функції. Цей вираз в ІДНФ представляє собою суму конституант одиниць:

 

    (3.12)

 

Конституанти одиниць пишуться як кон’юнкція, ІСДНФ представляє собою суму конституант, кожна з яких містить всі змінні у вигляді прямої або оберненої не більше одного разу. Логічна функція має єдиний булевий вираз у ІДНФ, що слідує з методики його отримання.

ІДНФ називається диз’юнктивним (складається з суми кон’юнкцій), ідеальні (всі кон’юнкції  містять один раз кожну змінну в прямому або інверсійному вигляді) і нормальні (дворівневі) для його реалізація вимагаються логічні елементи з двох типів: кон’юнктури  і диз'юнктори, передбачається, що вихідні змінні приходять у прямому та інверсному вигляді.

 

3.11 Диз'юнктивна нормальна форма (ДНФ)

Якщо вираз (3.10), то на всі або деякі із кон’юнкцій відсутні окремі змінні (прямої або оберненої форми), або ряд кон’юнкцій, які відображають конституанти одиниці відсутні, тоді така форма презентації логічного виразу називається диз'юнктивною нормальною формою (ДНФ).

Перемикання функції можна описати кількома бульевими виразами в ДНФ, один з яких є мінімальним (містить мінімум кон’юнкцій  і мінімум  вхідних змінних).

3.12 Ідеальна кон’юнктивна нормальна форма (ІКНФ) написання булевих виразів

У таблиці 3.4 перемикання функції на додаток до конституанти одиниці  містить конституанти нуля, К2, К3 та K7 (конституанта нуля є нульове значення перемикальної функції на один конкретний набір). Тільки для перемикальної функції 3-х змінних можуть бути вісім конституант нуля, якщо функція приймає значення 0 для всіх наборів. Конституанта нуля пишеться у вигляді диз'юнкцій. Для нашого прикладу (таблиця 3.4):

Логічний вираз у ІКНФ є константи нуля:

 

        (3.13)

 

ІКНФ називається кон’юнктивною (складається з диз’юнкцій), досконалою (всі диз'юнкції включають один раз кожну змінну у прямому або інверсному вигляді) і нормальною (дворівневою), для її реалізації вимагаються логічні елементи двох типів: кон’юнктури і диз’юнктури, передбачається, що вихідні змінні надходять у прямому або інверсному вигляді.

Логічна функція містить тільки єдиний булевий вираз в ІКНФ.

 

3.13 Кон’юнктивна нормальна форма (КНФ)

Якщо вираз (3.4), всі диз'юнкції або деякі з них не містять всіх змінних у прямому або оберненому вигляді, а також деякі диз'юнкції відсутні, тоді така форма представлення булевих виразів називається кон’юнктивною нормальною формою (КНФ).

Перемикальна функція може описуватись кількома булевими виразами в КНФ, один з яких є мінімальним (містить мінімум диз’юнкцій і мінімум вхідних змінних).

 

3.14 Мінімізація логічних функцій

Мінімізацією спрощення називається аналітичний вираз, який представляє перемикач (логічний) функції, щоб гарантувати, що булеві вирази перемикальної функції містять мінімальну кількість членів з мінімальною кількістю змінних.

Способи, щоб звести її до мінімуму:

– алгебраїчний;

–                   за допомогою діаграми Вейча (карти Карно).

 

3.14.1 Алгебраїчний спосіб мінімізації перемикальної функції (ПФ)

Інколи просте впровадження мінімізації логічних виразів перемикальної функції здійснюється за допомогою тотожності і теореми булевої алгебри.

Приклад 1. Вихідний логічний вираз:

 

.                          (3.14)

 

Застосовуючи теорему зв'язку, отримаємо логічний вираз:

 

,                                                   (3.15)

 

який рівносильний еквівалентний вихідному, але значно простіший.

Приклад 2 . Вихідний логічний вираз:

 

                         (3.16)

 

За допомогою тотожності  і теореми склеювання отримаємо більш простий вираз:

 

.                                                          (3.17)

 

Такі елементарні прийоми мінімізацій вдається використовувати, якщо оригінальний логічний вираз містить невелику кількість членів з невеликим числом змінних.

Наочним і зручним є зведення до мінімуму за допомогою діаграми Вейча (карти Карно).

 

3.14.2 Мінімізація перемикальних функцій за допомогою діаграми Вейча (карти Карно)

Вейча діаграми (карти Карно) [3, 11, 18] будуються так, щоб їх сусідні клітинки містили первинні перемикальні функції, різні значення однієї змінної: один член містить цю змінну прямої форми, а інший – в інверсної. Завдяки цьому відбувається наочне уявлення про різні варіанти для склеювання пов'язаних членів.

 

3.14.3 Мінімізація за допомогою діаграм Вейча

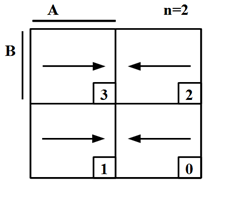
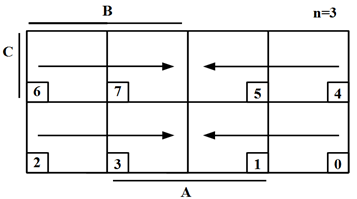
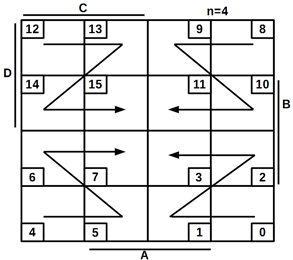
Початковий продукт для використання діаграм Вейча має таблиця істинності, в якій можливі набори змінних, упорядковані за зростанням або за спаданням своїх десяткових еквівалентів. Подання діаграми Вейча залежить від кількості змінних мінімізованої функції перемикання – n і впорядкованої множин змінних у таблиці. Якщо набори впорядковані за зростанням своїх десяткових еквівалентів, то діаграма Вейча для n = 2, 3, 4 має вигляд, показаний на рисунку 3.1. Кількість клітинок діаграми дорівнює кількості множин змінних:

 

                                                   (3.18)

 

Якщо , то  

Кожній клітинці відповідає набір змінних і має номер, вона дорівнює набору номера.

Рядки та стовпці діаграми помічені рискою, визначення набори, де змінні приймають одиничні значення (пряма форма). Рядки і стовпці, які не позначені  рискою, відповідають наборам, в яких ті ж змінні приймають нульове значення (обернений). Наприклад, для (рисунок. 3.1) двом лівим стовпцям відповідає одиничне значення змінної В (В входить у прямій формі) а для двох правих – нульове значення (В входить до оберненої форми).

а)                                                                   б)

в)

Рисунок. 3.1 – Діаграма Вейча: а) для двох змінних; б) для трьох змінних;
в) для чотирьох змінних

 

У клітинці значення теж записуються на відповідному наборі (нульове або одиничне). Якщо функція на певному наборі не визначена, тоді у клітинці діаграми ставиться тире.

Перемикальні функції вважаються невизначеними, якщо:

1) цей набір змінних в реальному логічному пристрої неможливий;

2) значення функції на даному наборі пасивне.

Після заповнення діаграми можна приступити безпосередньо до мінімізації, яку здійснюють за одиницями або нулями.

У першому випадку результатом мінімізації буде логічний вираз в ДНФ, а другий – у КНФ.

 

3.14.3.1 Загальні правила мінімізації

Мінімізація може здійснюватися за одиницями (нулями). У той же час:

1) Прилеглі до одиниць (нулів) діаграми умовно охоплюють (накривають) прямокутні контури. Кожний контур може містити 2, 4, 8, 16,... одиниць (нулів).

2) Одним контуром (покриттям) необхідно об'єднати максимальну кількість суміжних клітинок, які містять одиниці (нулі).

3) Необхідно, щоб кожна одиниця (нуль) накривалась хоча б один раз.

4) Одна і та ж одиниця (нуль) може бути покрита кілька разів різними контурами.

5) Верхні і нижні рядки діаграми вважаються суміжними, вони можуть бути створені, якщо умовно згорнути діаграму в горизонтальний циліндр.

6) Лівий та правий стовпчики вважаються також пов'язані – діаграми можуть умовно згорнути по вертикалі циліндри.

7) Кутові клітинки також вважаються пов'язаними – діаграми можна умовно згорнути в тор.

8) Перед виконанням мінімізації у клітинках, що містять тире (на даних наборах перемикальна функція невизначена), можна записати додаткові одиниці (нулі), що стимулює отримання більш простого кінцевого логічного виразу. Слід пам'ятати, що хоча б раз необхідно охоплювати лише основні одиниці (нулі). Додаткові одиниці (нулі) можуть збільшити сумарне число придбаних одиниць (нулів), які входять у покриття, таким чином зменшувати число змінних у результаті кон’юнкцій (диз’юнкцій).

9) Мінімізації логічний вираз виходить в ДНФ. Кількість кон’юнкцій в ДНФ (диз’юнкцій в КНФ) відповідає кількості контурів (накриттів).

10) В кожну кон’юнкцію (диз’юнкцію), входять тільки ті змінні, значення яких в межах контуру не змінюється (змінна приймає у покритті  лише одиничне значення або значення нуль (тільки у вигляді прямої або оберненої форми)).

У мінімізації одиниць в результаті кон’юнкції змінні, включені в прямій формі, якщо відповідні їм рядки і стовпці не позначені тире, в противному випадку диз’юнкція містить змінні в інверсному вигляді.

При зведенні до мінімуму 0 в результаті диз'юнкції змінні включені в прямій формі, якщо їх відповідні рядки та стовпці не позначені рискою, в іншому випадку диз'юнкція містить змінні у вигляді інверсному.

Щоб мінімізувати мінімальну ДНФ або КНФ, яка містить принаймні мінімальну кількість членів з мінімальною кількістю змінних, що входять до них, є змінними. Для цього необхідно мінімальним числом контурів охопити хоча б один раз кожну одиницю (нулів).

Рисунок 3.1 показує діаграми, коли булевих змінних Вейча n = 2, 3, 4. Для n > 4 діаграму, які містяться в [18]. Якщо набори змінних вихідної таблиці істинності впорядковані за убуванням своїх десяткових еквівалентів, то необхідно використовувати діаграми Вейча, наведені в [5, 6].

 

3.14.3.2 Приклади мінімізації перемикальних функцій за допомогою діаграм Вейча

Приклад 1. Контролювати можливу деформацію металевих конструкцій через перегрів їх в різних критичних точках, де встановлені чотири термодатчики, які позначаються ТД1, ТД2, ТД3, ТД4. Експериментальні дослідження конструкції показали, що в ході експлуатації можливі шість комбінацій спрацювання і неспрацювання датчиків. При цьому деформація конструкції виникала в наступних випадках:

1) спрацювали ТД4, ТД3 і не спрацювали ТД2 і ТД1;

2) спрацювали ТД4, ТД3, ТД2 і ТД1;

3) спрацювали ТД2 і не спрацювали ТД4, ТД3 і ТД1;

4) спрацювали ТД3, ТД2 і ТД1 і не спрацював ТД4;

У випадках, де:

5) спрацювали TД4, TД3, TД2 і не спрацював TД1;

6) спрацювали TД2, TД1 і не спрацював TД4, TД3;

деформація конструкції не виникає.

Відповідно до умов експлуатації конструкції інші структури комбінацій спрацювання і неспрацювання датчиків неможливі.

Необхідно розробити цифровий логічний пристрій, який включає в себе сигнал тривоги, якщо  відбувається  спрацювання небезпечної комбінації термодатчиків.

Позначимо цифрові сигнали на виході термодатчиків логічними змінними: TД4 →D; TД3 →P; → ТД2→В; ТД1→А, логічну функцію, яка має здійснити пристрій контролю – F. Складемо таблицю істинності, яка відображає логічну функцію (таблиця 3.8).

Таблиця 3.8 – Таблиця істинності

Діаграму Вейча, що відображає дану таблицю, показано на рисунку 3.2.

 

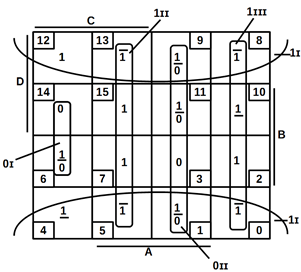
Рисунок. 3.2 – Діаграма Вейча, яка відображає мінімізацію логічної функції

 

Якщо будемо виробляти мінімізацію по одиницях, тоді в клітинці, яка містить тире, проставимо додаткові одиниці.

Основні одиниці накриваємо трьома контурами: 1-й контур (1I) формують клітинки спочатку першого і останнього рядка, 2 – й (1II) – клітинки 2-ої і 3 – колонки (1III) – 4-го стовпця.

Отриманий логічний вираз мінімізованої перемикальної функції, яка має вигляд:

 

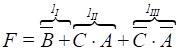                                        (3.19)

 

Цей вираз повинен відображатись в цифрових логічних пристроях, що включають сигнал тривоги.

Функція може бути зведена до мінімуму та нульового (0) значення. Для цього визначаємо клітинки з числами 1, 6, 9 і 11 нулями та покриття двох основних нулів двома прямокутниками, у тому числі два і чотири елементи (нуль). Перший прямокутник (0І) охоплює клітинки з числами 6,14, другий
(0II) – 1, 3, 11 і 9.

Отриманий логічний вираз  мінімізованої  перемикальної функції має вигляд:

 

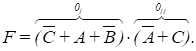                                               (3.20)

 

Вирази (3.11) і (3.12) еквівалентні, і слід використовувати той з них, який легше реалізувати на певному наборі  логічних елементів (базовий). Це питання буде розглядатися в наступних лекціях [3].

Приклад 2. Блок має бути пріоритетом переривання 2-х зовнішніх пристроїв: ЗП₁ і ЗП₂. ЗП і менше число вказує на вищий пріоритет, спрощену структуру дизайну показано в рисунку 3.3.

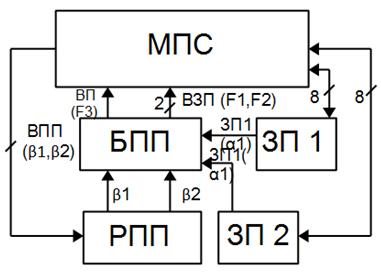
Рисунок 3.3 – Спрощений дизайн структури системи, яку проектуємо

 

На схемі – такі скорочення: МПС – мікропроцесорна система; ЗП –зовнішній пристрій; БПП – блок пріоритетних переривань; ВТП – вектор текучого переривання, що використання логічних змінних β₁, β₂ описує можливі стани
МП-системи при обслуговуванні запитів переривання від ВП (таблиця 3.7); РТП-регістр поточного переривання від ЗП₁, ЗП₂ (пам'ятає значення змінних, β₁ β₂); ЗП1, ЗП2 – перервати запити від ЗП₁, ЗП₂ (змінні описані α₁, α₂); TП – вимога до переривань (логічну функцію F₃); ВЗП – вектор запиту переривання, відображається комбінація значень булевих функцій F₁ і F₂ (таблиця 3.8).

Таблиця 3.7 – Опис можливих станів мікропроцесорної системи при обслуговуванні запитів переривання від зовнішнього пристрою

 

 

Таблиця 3.8 – Відображення вектора запиту переривання через комбінацію значень булевої функції F₁ і F₂.

 

 

MП-система періодично перевіряє значення TP сигналу функції (F₃). Якщо TП = 0 (запит на переривання відсутній), то значення функцій, F₁, F₂, є байдужим і МПС продовжує свою роботу. Якщо ТП = 1, МП – система аналізує значення МЗП векторів (поєднання функцій F₁, F₂) і вказує номер запиту переривання. Оскільки набір змінних β₁ = β₂ = 1 не є можливим (таблиця 3.6), то функції F₁, F₂, F₃ у таких випадках, на невизначені. Таким чином, завданням ЗПП є реалізація трьох логічних функцій F₁, F₂, F₃, кожна з яких визначається значенням чотирьох булевих змінних: α₁, α₂, β₂ β₁.

Логічний вираз мінімізує ПФ за формулою:

 

                                                    (3.21)

                                                                (3.22)

.                                                               (3.23)

Ми побудуємо таблицю істинності (таблиця 3.9) для вищеперелічених функцій.

 

Таблиця 3.9 – Таблиця істинності

 

Функції F₁, F₂, F₃ діаграми Вейча (рисунок. 3.4).

 

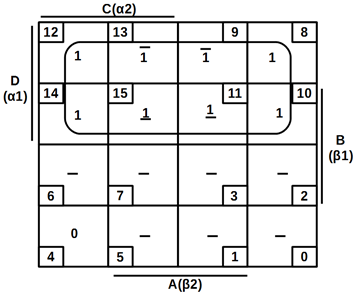
Рисунок 3.4 – Представлені функції F1, F2, F3

Отримані вирази (3.21 – 3.23) є цілком конкретними булевими тлумаченнями і якщо певні навички можуть бути отримані без  складання таблиці істинності і мінімізації перемикальної функції.

Таким чином, якщо F₃= 1, а в іншому випадку F₁ і F₂ байдужі, то запит від ВУ₁ у вигляді комбінації F₁= 0, F₂= 1 буде робити тільки тоді, коли α1 = 1. Значення в α₂ є байдужим, навіть якщо α₁ = 1 = α₂, α₁ має більш високий пріоритет. Якщо α₁ = 0 і F₃= 1, то це означає, що вимоги перервати через запит від ЗП₂ (α₂ = 1), написані вирази (3.11) могли б керуватися такими моментами F₃= 1 в двох випадках. По-перше, якщо прибув запит  від ЗП₁ (α₁ =1), хоча MP-система очікує запити, або обслуговує переривання від ЗП₂ (в обох випадках β₂ = 0, таблиця 3.8). По-друге, якщо надійшов запит від  ВУ₂ (α₂ = 1), в той час як MП-система знаходиться в режимі очікування (β₁ = β₂ = 0). Вищесказане представляє два установчі вирази (3.21).

У другому прикладі ми пройшли 2 етапи синтезу комбінаційних цифрових електронних пристроїв:

1. Презентація перемикальних функцій у формі, яка є джерелом для вибраного методу мінімізації в нашому випадку, у вигляді таблиць істинності  і діаграми Вейча.

2. Отримання  мінімальної ДНФ для кожного виходу комбінаційної схеми.

 

3.14.4 Мінімізація перемикальних функцій за допомогою карт Карно

Рисунок 3.5 показує приклад карти Карно для перемикальної функції чотирьох змінних (n= 4).

Кожна клітинка в картах Карно так само, як і в діаграмах Вейча, відповідає певному набору змінних. Сусідні клітини відповідають наборам, відрізняються значенням однієї із змінних. Значення конкретної змінної або комбінація (product) змінної у вигляді прямого або оберненого позначаються в кожному рядку та стовпчику.

Клітинки, позначені змінними у прямій формі, відповідають наборам, де ці змінні приймають одиничні значення, а клітинки, позначені змінними в інверсній формі, наборами, де ці змінні дорівнюють нулю.

Карту Карно зручно використовувати, якщо перемикальна функція задається у вигляді логічних виразів у СДНФ.

Наприклад:

 

 ‚ ƒ

                                 (3.24)

„ … †

 

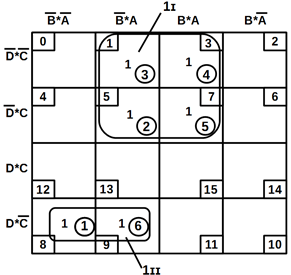
Рисунок 3.5 – Мінімізація перемикальних функцій 4-x змінних за допомогою карт Карно

 

Правила мінімізації за допомогою карти Карно в основному аналогічні правилам, викладеним при розгляді діаграма Вейча. Різниця полягає у наповненні карти Карно одиницями. Якщо діаграма Вейча наповнена одиницями відповідно до кількості наборів, де оригінальні перемикальні функції приймають одиничне значення, тоді в карті Карно одиниці проставляються в клітинках, лежачи на перетині рядків і стовпців. Відмічені комбінації змінних, які при їх перемноженні дають відповідний запис конституанти одиниці (кон'юнкції) у логічному виразі мінімізованої функції (3.14). На рисунку 3.5 наведено приклад заповнення карти Карно з виразу (3.14), яка містить шість одиниць конституант.

Булеві вирази мінімізованої ПФ має такий вигляд:

 

.                                            (3.25)

 

Інші приклади використання Карно і Вейча наведені в [3, 18].