Тема 2. Дискретизація аналогових сигналів

 

В управлінні інформаційними системами часто виникає завдання обробки аналогових повідомлень, які знімаються з аналогових датчиків. Введення цієї інформації в комп'ютер, каталог, обробка в цифровій формі, виконує дискретизація (квантування) аналогових сигналів.

Найбільш поширені і загальноприйняті методи обробки сигналів у подальших викладах.

Розрізняти три види дискретизації:

-                   за рівнем;

-                   за часом;

-                   за рівнем і часом (комбінована).

Розглянемо кожен з цих видів квантування більш докладно.

 

2.1 Квантування за рівнем

Вважаємо, що інформація відображається аналоговою (безперервною) напругою U (t), яка повільно змінюється відповідно до закону, представлена на рисунку 2.1 [2].

Миттєві значення напруги  знаходяться у діапазоні . Під час виконання операції квантування на рівні діапазон змінювання  значень безперервних величин ділиться на кілька рівнів Nу, включаючи 0. Кількість Nу визначається з виразу

 

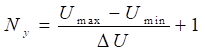,                                             (2.1)

 

де, – значення кроку квантування за рівнем. При цьому останнє є постійною величиною  і визначає необхідну похибку дискретизації. У нашому прикладі N_у = 5. Кожен рівень пронумерований у десятковій системі числення. Робота квантування приводиться до наступного: вона визначає моменти часу, коли вхідний аналоговий сигнал досягає наступного дискретного рівня.

 

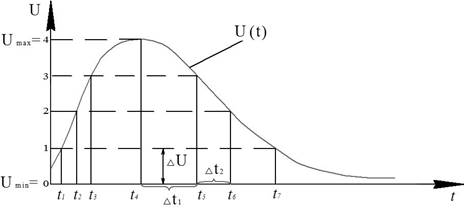
Рисунок. 2.1 – Квантування сигналу за рівнем

 

Ці моменти позначені t₀, t₁, t₂, t₃... , зрозуміло, що коли при нелінійному вхідному сигналі інтервал між суміжними тимчасовими відрахунками є  змінною величиною . Прикладом пристроїв, в яких відбувається квантування за рівнем, є релейні (порогові) пристрої.

 

2.2 Квантування за часом

Квантування операції  за часом (рисунок 2.2) постійного вхідного сигналу замінено решітчастим (дискретним), який знімається з виходу квантування у дискретні моменти часу t₁, t₂, t₃…, інтервал між сусідніми моментами часу

 

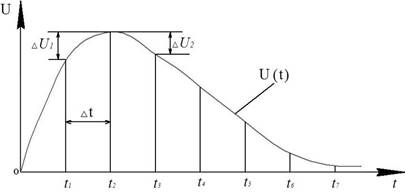
Рисунок 2.2 – Квантування сигналу за часом

Зрозуміло, що різниця між сусідніми значеннями вхідного сигналу у нелінійному законі зміни вхідної напруги змінна величина  Прикладом пристроїв, в яких здійснюється квантування за часом, є імпульсні системи автоматичного керування [20].

 

2.3 Квантування за рівнем і за часом

Робота такого перетворювача (рисунок 2.3) призводить до того, що з безперервного сигналу періодично проводяться вибірки миттєвих значень. Проміжок часу між суміжними вибірками , кожна вибірка округлюється перетворювачем до найближчого рівня квантування, отримана від дискретизації за рівнем. Інтервал між суміжними рівнями .

 

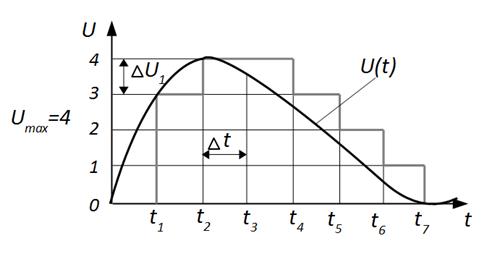
Рисунок 2.3 – Квантування сигналу за рівнем і часом

 

Значення за рівнем представлене у десятковій або двійковій системі числення (десятковий або двійковий код). Код за рівнем, у свою чергу, видається цифровим сигналом. Вихідний сигнал має ступінчату форму і з ступенем точності, яка відповідає аналогові напруги. На цьому принципі працюють електронні аналого-цифрові перетворювачі (АЦП) [10, 13].

 

 

 

2.4 Розрахунок похибки АЦП

На виході АЦП кожному дискретному значенню відповідає поєднання двійкового коду, число розрядів якого (включаючи 0) позначається буквою N_p . Вибір N_P проводиться у відповідності до вимог:

 

                                                           (2.2)

 

Кількість дискретних значень N_Д (рівень квантування) залежить від похибки квантування за рівнем;

абсолютної похибки, коли з'являються квантування за рівнем:

 

                                                           (2.3)

 

де ∆U – величина кроку квантування за рівнем дорівнює:

 

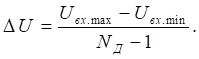                                              (2.4)

 

З вищенаписаного випливає, що максимальне відношення абсолютної похибки дорівнює половині кроку квантування за рівнем. Відносна похибка квантування за рівнем:

 

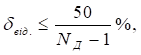                                                 (2.5)

 

де N_д – число дискретних значень вихідних величин (рівнів квантування). У рівнянні (2.5) з N_Д віднімається одиниця, тому що одне з дискретних значень (рівнів) є нуль (цифра 2.3). Отже, необхідну кількість рівнів дискретних значень, які відображають неперервну функцію з вказаною точністю, визначається з виразу:

 

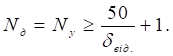                                                    (2.6)

 

Приклад розрахунку АЦП:

Задано значення відносної похибки .

Необхідно визначити АЦП, що задовольняє заданому значенню

Визначити кількість рівнів квантування (число дискретних значень):

Вибираємо кількість розрядів АЦП N_{P Д. К}. = 5, що задовольняє вираз (2.5): 25=32>26.

 

2.5 Вибір величини кроку квантування за часом

Величина кроку квантування за часом ∆t визначає необхідну продуктивність АЦП, розрахованого відповідно до теореми вибірки відліку (теорема Котельнікова):

 

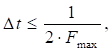                                                        (2.7)

 

де F_max – частота  вищих гармонік вхідного аналогового сигналу частотного спектра. Іншими словами, при переміщенні до дискретних величин  найбільших для гармонійних компонентів вхідного сигналу має мінімальний період (максимальна частота), необхідно прийняти, принаймні, два відрахунки.

Будь-які АЦП є інерційним пристроєм, вони мають кінцевий час перетворення t_prb, а також відповідають потрібному значенню ∆t.

Якщо аналоговий вхідний сигнал змінюється досить швидко і в АЦП є неналежна робота, то може з'явитися похибка, що зміна часу перетворення АЦП вхідного сигналу еквівалентно зміни  вихідного ДК, більш ніж на одиницю МЗР. Для боротьби з цим явищем використовується пристрій вибірки-збереження, що пам'ятає миттєве значення вхідного аналогового сигналу на даний момент тимчасової вибірки і підтримує значення постійним до наступної вибірки.

При проектуванні на комп'ютеризований системи часто виникає обернена задача: перетворення цифрового сигналу в аналоговий (безперервний). Для цього застосовують цифро-аналогові перетворювачі (ЦАП).