Тема 1. Інформаційні основи цифрових автоматів

 

1.1 Інформація та загальні принципи її перетворення

В основу обчислювальної техніки закладені інформаційні процеси, пов'язані зі збором та обробкою інформації, її передачею, зберіганням, розповсюдженням, відображенням, записом, читанням, і т. д. З усіх цих процесів у кінцевому підсумку можна виділити чотири основних процеси або процедури: отримання інформації, трансфер, зберігання та переробка. Реалізація всіх цих процедур у загалом супроводжується перетворенням фізичного носія інформації та форми його представлення.

Не зупиняючись на складній проблемі формалізованого визначення поняття інформації, будемо вважати, що інформація – це є відомості про ті чи інші явища та об'єкти (наприклад: звіти про погоду, археологічні, політичні тощо), точніше – відомості про певні властивості або параметри цих явищ чи об'єктів та про залежності між цими властивостями.

Інформація, втілена та зафіксована у деякій матеріальній формі, називається повідомленням, а фізичні засоби передачі повідомлення –  сигналом. Або іншим чином: сигнал – це процес зміни у часі деякого фізичного параметра S (t) будь-якого об'єкта, який використовується для відображення, реєстрації та передачі повідомлення.

Характер зміни сигналу з часом може бути представлений графічно, у вигляді осцилограми, за допомогою таблиці, в яку вносять значення Si в i - ті моменти часу, аналітично.

Теоретичні дослідження сигналу і його розрахунки здійснюються з використанням методів математичного опису, тобто створенням математичної моделі сигналу. При створенні такої моделі описуються тільки властивості, які здаються об'єктивно-важливими, при цьому ігнорується – велика кількість другорядних ознак. У якості математичної моделі сигнал може бути прийнятий, наприклад, як функціональна залежність, його аргумент, є часом S = (f) (t).

З цієї моделі, зрозуміло, що причиною зміни S є не сам час, а деяка інша фізична величина. Тому точніше сказати, що маркування сигналів через S (t), q (t)…. застосовує модель, яка описує зміну значення S, q,... в часі.

Існують різні типи сигналів:

-безперервний, тобто аналоговий;

- дискретні;

- квантовані;

- кодовані (цифровий);

- модульовані;

- імпульсні.

Практично при будь-якій обробці інформації здійснюються ті чи інші перетворення сигналів.

Перетворення сигналів застосовується тоді, коли змінюється носій інформації, або функції, яка передається за певним законом і  забезпечує індивідуальну відповідність між входом і виходом.

У випадку безперервного вхідного сигналу найбільш часто використовується процедура зміни типу сигналу – її дискретизації.

Дискретний сигнал описує функцію решітки (послідовність часових рядів) , в якому значення в X може приймати будь-які значення з проміжку , в той час як незалежна змінна (n) приймає тільки дискретні значення
n = 0; 1; 2;... t -інтервал (крок) дискретизації. Дискретизація безперервного сигналу S(-t) може вироблятись відповідно до рівня. Останній випадок дискретизації, зазвичай, називають як параметр квантування.

Коли дискретизація сигналу S (t) здійснюється в часі, то безперервний сигнал S (t) замінюється на послідовність імпульсних сигналів, амплітуда яких відповідає значенню безперервного сигналу в дискретні моменти часу nt.

У цьому випадку значення t рівне часовому інтервалу, який потім  є циклічна частота,  і  відповідно кругова частота.

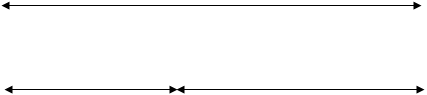
Приймаємо, що сигнал S (t) заданий або графічно або у вигляді таблиці, де внесені його значення у межах періоду часу Т через певні проміжки часу, тобто період Т поділений в даному випадку на 2 (n) рівних частини (рисунок. 1.1).

 

         S                                                          Тоді абсциси точок розподілу будуть

                                                         рівні: , а ординати

                                                                      в цих точках:

                                                                              де k = 0, 1, 2,… 2n,

      S1   S2      S3                   S2n–i            S2n                 

 

 

                                               t

       t1     t2        t3                                 t2n–i     t2n

Рисунок 1.1 – Дискретизація сигналу

 

де Sk – значення амплітуди сигналу S(t) (k)-ий момент часу.

Якщо при безперервному сигналі вираз є такий:  то після дискретизації в часі  цей сигнал описується рівнянням:

 

                                                (1.1)

 

У результаті дискретизації первісна функція S (t) замінюється поєднанням окремих значень Sk, що може бути використано для відновлення первісної функції S(-t) з деяким запасом похибки. Функція, отримана в результаті   такого відновлення (інтерполяції), називається відтворюючою. Для відтворення функції, яку необхідно представити, найбільш часто використовують степеневі алгебраїчні  многочлени у вигляді:

 

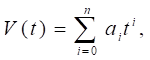                                                         (1.2)

де n – степінь многочлена; a_i  – дійсні коефіцієнти.

При дискретизації сигналів необхідно вирішити, як часто потрібно робити розрахунки функцій, тобто визначити, який повинен бути крок (квантування) дискретизації.

Відповідно до теореми В.А. Котельнікова, якщо функція S(t) не містить частот вищих за F_m, то вона повністю визначається їх миттєвими значеннями у момент часу, розташованими на величину  – крок  час дискретизації;

– миттєві значення сигналу S(t), k-ої відлікової точки:

 

                                      (1.3)

 

З теореми випливає, що для однозначного представлення функції з обмеженим діапазоном  на  інтервалі часу  Т достатньо мати деякі n  значення функції, де:

 

                                                (1.4)

 

Коли виконується ця рівність, безперервна і дискретна функції оборотні між собою, тобто тотожні. Таким чином, довільний сигнал,  діапазон якого не містить частот вище F_m, може бути представлений у вигляді послідовності імпульсів, амплітуди яких дорівнюють значенню вихідного сигналу у дискретні моменти часу kt – і проміжки часу між ними t = 1/2 Fm.

З приведених вище формулювань  теореми Котельнікова  слідує, що для вибору оптимального кроку дискретизації  необхідно зробити кількісну оцінку всіх значних гармонік спектрального розкладу непереривного  оригінального безперервного сигналу для надходження значень F_m , тобто m.

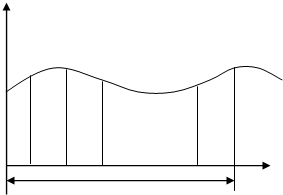
Розглянемо параметр сигналу квантування [1].

У діапазоні неперервних величин функція f(t) вибирається скінченна кількість дискретних значень функцій, наприклад, рівномірно розподілених на весь діапазон. У будь-який час значення функції f(t) замінюється з найближчого дискретного параметра значення функції, тим самим функція набуває ступінчатого зовнішнього вигляду. (рисунок 1.2).

 

 

Рисунок 1.2 – Ступінчатий зовнішній вигляд функції

 

Крок квантування параметра є різниця між сусідніми дискретними значеннями функції.

Для рівномірного квантування крок квантування рівний:

 

                                     (1.5)

 

де q – кількість кроків квантування.

Абсолютна похибка квантування параметру може змінюватись від 0 до К/2. Середньоквадратична похибка квантування у разі рівномірного розподілу приведеної похибки від 0 до 0,5 К дорівнює:

 

                                                 (1.6)

Коли значення параметра квантування сигналу отримує деяке число (код) із скінченної множини вибраної системи числення, то виконується процедура кодування сигналу.

Закодовані таким чином сигнали зазвичай називають цифровим сигналом. Втім, ми повинні мати на увазі, що кодування в широкому сенсі цього слова є будь-які перетворення повідомлень на певний сигнал, які створюють між ними однозначну відповідність.

Цифровий сигнал описує функцію квантової решітки (квантована послідовність, квантування часових рядів) Xw (nt), яка приймає ряд дискретних значень, рівнів квантування (h) 1, (h) 2, (h) 3... hk,  при цьому незалежної змінної
n = 0, 1, 2,... Кожному із рівнів квантування присвоюється номер, таким чином сигнал кодується. Тому передача або обробка відліку цифрового кодованого сигналу зводиться до операцій над безрозмірними числами (кодами). Показ сигналу у цифровій формі  майже завжди має значну перевагу при передачі, зберіганні та обробці інформації.

Отже, в цьому випадку інформація кодується кінцевим набором символів (цифр, букв), які вибираються  з деякого кінцевого алфавіту. Будь-які скінченні послідовності сигналів називаються словом в  цьому алфавіті. Метод зображень будь-якого числа, використовуючи обмежену кількість цифр, називається системою числення.

Кодування аналогового сигналу проводиться за допомогою різних видів аналого-цифрових перетворювачів (АЦП). Зворотний порядок реалізується цифрово-аналоговими перетворювачами (ЦАП). Для перетворення сигналів, зокрема, використовуються різні модулятори і демодулятори, вони широко використовуються в так званих модемах, в яких комп'ютери підключаються до різних типів  обчислювальних мереж. Часто перетворюють і фізичну природу сигналу. Зокрема, перетворення оптичного сигналу в електричний і, навпаки, виконується за допомогою різних оптоелектронних приладів.

 

 

1.2 Системи числення

У позиційних системах числення одна і та ж цифра (числовий знак) у записі числа набуває різних значень залежно від своєї позиції. Таким чином, позиція цифри має вагу у числі. Здебільшого вага кожної позиції кратна деякому натуральному числу b, b > 1, яке називається основою системи числення.

Крім звичної нам десяткової, також поширені системи числення з основами:

2 — двійкова (у дискретній математиці, інформатиці, програмуванні)

8 — вісімкова (у програмуванні);

12 — дванадцяткова (мала широке застосування у давнину, подекуди використовується і нині);

16 — шістнадцяткова (поширена у програмуванні, а також для кодування шрифтів);

60 — шістдесяткова (для виміру кутів і, зокрема, довготи та широти).

Переведення довільної позиційної системи числення до десяткової.

Якщо число у системі числення з основою b дорівнює:

 

                                                        (1.7)

 

то для переведення його до десяткової системи обчислюють наступну суму:

 

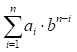,                                                               (1.8)

 

або, більш наочно:

 

,                          (1.9)

 

або, нарешті, у вигляді схеми Горнера:

 

                                 (1.10)

 

Приклад:

1011002 = 1 · 25 + 0 · 24 + 1 · 23 + 1 · 22 + 0 · 21 + 0 · 1 =

= 1 · 32 + 0 · 16 + 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 32 + 8 + 4 + 0 = 4410.

Переведення із десяткової до довільної позиційної системи числення.

Для переведення потрібно ділити число із залишком на основу системи числення, допоки частка не стане меншою за основу.

Приклад:

4410 переведемо до двійкової системи:

44 ділимо на 2. частка 22, залишок 0;

22 ділимо на 2. частка 11, залишок 0;

11 ділимо на 2. частка 5, залишок 1;

5 ділимо на 2. частка 2, залишок 1;

2 ділимо на 2. частка 1, залишок 0.

Частка менша двох, ділення закінчено. Тепер записуємо усі залишки, починаючи з останнього, і останню частку від ділення зліва направо, отримаємо число 1011002.

Переведення із двійкової у вісімкову та шістнадцяткову системи і, навпаки.

Для цього типу операцій існує спрощений алгоритм.

Для вісімкової — розбиваємо числа на триплети, перетворюючи триплети згідно  таблицею 1.1.

 

Таблиця 1.1 – Переведення із двійкової у вісімкову систему числення

 

Для шістнадцяткової — розбиваємо на квартети (тетраедри), перетворюючи згідно з таблицею1.2.

 

Таблиця 1.2 – Переведення із двійкової у шістнадцяткову систему числення

 

Приклад 1.

Перетворимо 1011002

у вісімкову — 101 100 → 548,

у шістнадцяткову — 0010 1100 → 2C16.

Приклад 2.

Перетворимо до двійкової системи

768 → 111 1102

3E16 → 0011 11102.

Перетворення дійсних чисел. Для переведення чисел із системи числення з основою p в систему числення з основою q з використанням арифметики старої системи числення з основою p потрібно:

§      для переведення цілої частини:

послідовно число, записане у системі основою p ділити на основу нової системи числення, виділяючи остачі. Останні записані у зворотному порядку, будуть утворювати число в новій системі числення;

§      для переведення дробової частини:

послідовно дробову частину множити на основу нової системи числення, виділяючи цілі частини, які й будуть утворювати запис дробової частини числа у новій системі числення.

Цим самим правилом зручно користуватися в разі переведення з десяткової системи числення, тому що її арифметика для нас звичніша.

Приклади: 999,3510=1111100111,010112

§      для цілої частини:

§      для дробової частини:

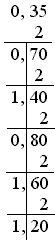
Арифметичні операції над числами у двійковій системі.

Додавання двох чисел у двійковій системі можна виконувати стовпцем, складаючи або дві цифри молодшого розряду, або дві цифри чисел, які додаються в даному розряді, і одиниці перенесення з сусіднього молодшого розряду. Наприклад:

 1111101

 + 101101.01

 11011.01

 -------------------

 1001000.10.

Числа у двійковій системі віднімаються аналогічно числам у десятковій системі. При відніманні чисел в даному розряді, якщо цифра, яка зменшується, менша цифри числа, що віднімається, позичають одиницю з наступного старшого розряду. При цьому одиниця, яка позичається із старшого розряду, рівна двом одиницям даного розряду.

Наприклад:

 10101.11

 - 1011.01

 ---------------

 1010.10

Подання цілих чисел у комп’ютері.

Для подання чисел у пам’яті комп’ютера використовують спеціальні двійкові коди: прямий, обернений та доповняльний.

Прямий код. Для його одержання треба у двійковому цілому числі знак „+” замінити символом „0”, а знак „–” – символом 1. Наприклад, для двійкового числа Х=-1001111 його прямим кодом буде [X] пр.=1.1001111. Тут крапка відокремлює знак числа від його цифрової частини.

Обернений код цілого числа. Для додатніх чисел обернений код співпадає з прямим.

Для оберненого коду нуль має два зображення:

 

.                                  (1.11)

 

Доповняльний код. Для додатніх чисел доповняльний код співпадає з прямим. Для від’ємного числа доповняльний код визначається за співвідношенням:

 

                                                   (1.12)

 

Доповняльний код цілого від’ємного числа можна одержати за таким алгоритмом:

1)           у знаковий розряд записати одиницю;

2)           у цифрових розрядах одиниці замінити нулями, а нулі – одиницями;

3)           до наймолодшого розряду одержаного результату (обернений код) додати 1.

Приклад 2.

Знайти доповняльний код від’ємного числа –10110, записаного у байтове машинне слово.

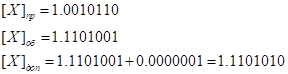
Обернений та доповняльний коди використовуються для виконання арифметичних дій. При цьому дію віднімання замінюють дією додавання обернених або доповняльних кодів.

 

Система                                               (1.13)

                                         (1.14)

                                     (1.15)

 

Подання дійсних чисел у комп’ютері. Для збільшення діапазону подання чисел у комп’ютері було запропоновано подавати числа в режимі з плаваючою крапкою:

 

                                                      (1.16)

 

де: m – мантиса; p – характеристика або порядок.

Мантиса задає значущі цифри числа, а порядок вказує місцезнаходження крапки, яка відділяє цілу частину від дробової.

У комп’ютерах використовують нормалізоване подання числа:

 

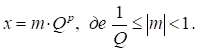                                    (1.17)

 

Машинне слово ділиться на два основних поля. В одному полі записується мантиса числа, в другому – порядок числа.

У пам’яті комп’ютера мантиса подається як ціле число, що містить тільки значущі цифри (0 і крапка не зберігаються). Отже, внутрішнє подання у комп’ютері дійсного числа зводиться до подання пари чисел: порядку і мантиси.

При цьому використовується машинний порядок. Машинний порядок М_р зміщений відносно математичного р і має тільки додатні значення. Зміщення z вибирають так, щоб мінімальному математичному порядку р відповідав нуль:

 

                                            (1.18)

 

Для запису внутрішнього подання дійсного десяткового числа в машинному слові (числовому регістрі) потрібно:

1)               перевести модуль даного числа у війкову систему числення з
k-значущими цифрами, k – кількість розрядів машинного слова, відведених для запису мантиси;

2)               нормалізувати війкове число;

3)               знайти машинний порядок у двійковій системі числення;

4)               враховуючи знак числа, записати представлення в машинному слові.

Приклад. Машинне слово складається із 4-ох байтів, перший з яких відводиться для запису М_р і знаку числа. Подати у цьому слові десяткове число 53287,625.

1.           53287,62510=D027,A16=1101000000100111,1012;

2.           1101000000100111,1012=0,110100000010011110110210000.

3.           Для запису машинного порядку числа відведено 7 двійкових розрядів. Оскільки 27=128, то математичний порядок може мати 128 значень і бути як додатнім, так і від’ємним. Тому доцільно ці значення поділити порівну між невід’ємними (від 0 до 63) та від’ємними (від –64 до –1) числами. Тоді, машинний порядок дорівнює М_р = р + 64 або у двійковій системі числення: , оскільки 6410=10000002. Математичний порядок р=100002. Отже, М_р(2)=10100002.

4.        Записуємо подання числа у 32-розрядному машинному слові, пам’ятаючи, що мантиса – правильний дріб (тому записується, починаючи з лівих розрядів, відведених для мантиси).

 

 

1.3 Двійкові коди

Двійкові числа в обчислювальних пристроях розміщуються у комірках пам'яті, причому для кожного розряду числа виділяється окрема комірка, що зберігає один біт інформації. Сукупність комірок, призначених для розміщення одного двійкового числа, називають розрядною сіткою. Довжина розрядної сітки (число комірок n у розрядній сітці) обмежена і залежить від конструктивних особливостей обчислювального пристрою. Більшість існуючих електронних обчислювальних пристроїв мають розрядні сітки, що містять 16, 32 або 64 комірки.

Розміщення розрядів числа у розрядній сітці може відбуватися різними способами. Спосіб розміщення визначається формою подання двійкових чисел у ЕОМ. Розрізняють дві форми подання двійкових чисел: із фіксованою комою і з «плавучою» комою. Іноді ці форми називають відповідно природними і напівлогарифмічними.

Припустимо, що в розрядній сітці необхідно розмістити двійкове число, яке містить цілу і дробову частини. Якщо для розміщення цілої частини числа виділяється k комірок n-розрядної сітки, то (якщо не враховувати знак) для розміщення дробової частини залишиться n-k вільних комірок (рисунок 1.3).

Така форма подання двійкових чисел називається формою з фіксованою комою. Дійсно, положення коми строго фіксоване стосовно розрядної сітки. Якщо кількість розрядів у дробовій частині числа перевищує n-k, то деякі молодші розряди виходять за межі розрядної сітки і не будуть сприйматися обчислювальним пристроєм. Отже, будь-яке двійкове число, менше одиниці молодшого розряду розрядної сітки, сприймається як нуль і називається машинним нулем.

		n
Знак		1	0	1	0		1	1	0	1	1	0
		k				n-k

Рисунок 1.3 – Форма подання двійкових чисел із фіксованою комою

 

У результаті відкидання молодших розрядів дробової частини числа, розташованої за межами розрядної сітки, виникає похибка подання. Максимальне значення абсолютної похибки подання не перевищує одиниці молодшого розряду сітки.

В універсальних ЕОМ форма з фіксованою комою, у зв'язку з властивою їй низькою точністю, застосовується лише для подання цілих чисел. Основною є форма подання чисел з «плавучою» комою. Її використання дозволяє суттєво розширити діапазон і зменшити відносну похибку.

У цій формі числа подаються у вигляді суми деякого ступеня основи системи числення (який називається характеристикою числа) і цифрової частини, що має вигляд правильного дробу:

 

,                                                (1.19)

 

де p звуть порядком числа, а правильний дріб a – його мантисою. Мантиса і порядок є знаковими числами. Тому для позначення знаків у розрядній сітці відводяться два додаткові розряди. Знак усього числа співпадає із знаком мантиси.

При запису двійкового числа у показовій формі в розрядній сітці використовуються дві групи розрядів (без урахування знакових розрядів мантиси і порядку). Перша група (k розрядів) призначена для розміщення коду мантиси, друга (n-k розрядів) – для розміщення коду порядку (рисунок 1.4).

		n
Знак мантиси	1		0	1	0	1		1	0	1	1	0	Знак порядку
		k					n-k

Рисунок 1.4 – Форма подання двійкових чисел із „плавучою” комою

 

Отже, мантиса числа може мати необмежену кількість різних значень, менших за одиницю, при відповідних значеннях порядку (тобто кома може «плавати»). З усієї кількості подань числа у показовій формі те його подання, що не має в старшому розряді мантиси нуля, називають нормалізованим. Всі інші подання є ненормалізованими. У нормалізованій формі значення мантиси завжди більші або дорівнюють 1/2, але не перевищують одиниці.

В обчислювальних пристроях із «плавучою» комою усі числа зберігаються у нормалізованому вигляді, при цьому не втрачаються молодші розряди мантиси і підвищується точність обчислень. Якщо після виконання будь-якої арифметичної операції результат виявляється ненормалізованим, то перед занесенням числа в пам’ять виконують його нормалізацію, тобто зсув мантиси ліворуч на відповідну кількість розрядів і зменшення порядку числа на відповідну кількість одиниць.

Показова форма подання чисел має і свої вади, найбільшого з яких є порівняно висока складність виконання арифметичних операцій, а отже, і більша вимогливість до ресурсів обчислювального пристрою. Це обмежує її застосування, наприклад, у спеціалізованих радіотехнічних обчислювальних пристроях, у системах управління технологічними процесами та обробки вимірювальної інформації у реальному часі.

Залежно від способу обробки бітів, розміщених у розрядній сітці, розрізняють два види кодів: паралельний, коли в кожний момент часу всі розряди сітки доступні для обробки, і послідовний, коли в кожний момент часу доступний один розряд сітки. Числа, подані паралельним кодом, доступні за один такт, а числа, подані послідовним кодом, – за n тактів, де n – розрядність сітки. Якщо розрядність числа перевищує довжину сітки, то його обробка ведеться частинами.

Натуральним кодом називають подання числа як цілого беззнакового у двійковій системі числення. Діапазон подання чисел у натуральному коді для
n- розрядної сітки становить від 0 до 2ⁿ–1, тобто для 8-розрядної сітки – від 0 до 255.

Для подання цілих знакових чисел використовують прямий, обернений і додатковий коди. Старший розряд сітки є знаковим. Значення цього розряду дорівнює 0 для додатних чисел і 1 – для від’ємних. В інших розрядах розміщується модуль числа.

Якщо до натурального коду цілого числа додати знаковий розряд, то одержуємо запис числа у прямому коді (ПК). Домовимося знаковий розряд розташовувати зліва і відокремлювати від розрядів модуля числа крапкою, наприклад: + 6₍₁₀₎ = 0. 110_(ПК); – 6₍₁₀₎ = 1. 110_(ПК).

Використання ПК забезпечує виконання операції додавання двох додатніх чисел звичайним способом без будь-яких складностей – не варто лише робити перенос одиниці старшого розряду модуля суми у знаковий розряд. Тобто при виконанні арифметичних операцій над ПК двійкових чисел знаковий розряд і розряди модуля не можна розглядати як єдине ціле. У цьому можна переконатися, розглянувши такий приклад:

Однак виконання операції віднімання одного числа від іншого шляхом безпосереднього додавання їхніх ПК неможливо. Неважко також помітити, що в ПК нуль має два можливі зображення: – 0 = 1.000... і + 0 = 0.000..., що ускладнює інтерпретацію результатів виконання арифметичних операцій у ЕОМ.

Іншою формою запису двійкових чисел є обернений код (ОК). ОК двійкового від’ємного числа утворюється з ПК рівного йому за модулем додатнього числа шляхом інвертування значень усіх його розрядів. Або: ОК від’ємного числа утворюється шляхом інверсії всіх розрядів модуля цього числа, записаного у ПК. Знаковий розряд при цьому зберігає значення 1. Наприклад, 6₍₁₀₎ = 1.110_(ПК) =1.001_(ОК).

При виконанні арифметичних операцій над двійковими числами, поданими в ОК, знаковий розряд і розряд модуля числа можна розглядати як єдине ціле (перенос одиниці зі старшого розряду модуля суми у знаковий розряд не приводить до помилкового результату), але нуль як і раніше має два зображення – «додатнє» і «від’ємне». Слід зазначити, що отриманий при додаванні від’ємний результат також утворюється в ОК. У цьому випадку число може бути перетворене у ПК інверсією всіх значущих розрядів (розрядів модуля). Наприклад:

0.110

+1.001

1.111(ОК) = 1.000(ПК)

(+6) + (–6) = (–0)

Додавання двійкових чисел із знаком. Очевидно, що при додаванні чисел із знаком можуть виникати переноси одиниці із старшого розряду модуля суми до знакового розряду (домовимося позначати його Р₁) та із знакового розряду – ліворуч за межі розрядної сітки, у розряд переповнення (Р₂). Через використання розглянутих раніше кодів, у яких знак числа позначається тими ж цифрами, що і розряди модуля, переповнення розрядної сітки може виникати навіть у випадку додавання чисел із різними знаками, коли модуль результату не перевищує модуля будь-якого операнда. При додаванні ж двох від’ємних чисел перенесення одиниці до розряду переповнення відбувається завжди.

При виникненні переповнення розрядної сітки для одержання правильного результату додавання необхідно застосовувати таке правило:

·    якщо Р₁ Å Р₂ = 0, одиниця в розряді переповнення ігнорується (відкидається);

·    якщо Р1 Å Р2 = 1, необхідно зсунути число на один розряд праворуч (або зсунути позицію точки на один розряд ліворуч).

Додавання дробових і цілих двійкових чисел, поданих у формі з фіксованою комою, відбувається однаково, тобто порядок додавання не залежить від розташування коми. Тому операцію додавання розглянемо на прикладі додавання цілих чисел.

Приклади:

1) Додавання двох додатніх чисел (без переповнення розрядної сітки):

 

 

Р₁Å Р₂ = 0 – результат коректний і остаточний.

2) Додавання двох додатніх чисел (з переповненням розрядної сітки):

 

Р₁ Å Р₂ = 1. Результат некоректний, тому що відбулося переповнення розрядної сітки. Зсуваючи число на один розряд праворуч, остаточно маємо: 0.100000_(ПК) = 32₍₁₀₎.

3) Додавання двох чисел із різними знаками (без переповнення розрядної сітки):

 

Р₁ Å Р₂ = 0. Результат коректний, але тому, що він є від’ємним, для перевірки правильності розв’язання необхідно перетворити його у прямий код. Остаточно маємо 1.100111_(ПК) = 39_(10).

4) Додавання двох чисел, рівних за модулем і різних за знаком:

 

Р₁Å Р₂ = 0. Результат коректний, якщо не брати до уваги одиницю у розряді переповнення.

Додавання двох від’ємних чисел виконується аналогічно прикладам 1, 2 (у залежності від значення виразу Р₁ Å Р₂. Тому, що результат у цьому випадку завжди від’ємний, для перевірки правильності розв’язання необхідно перетворити його у прямий код, аналогічно прикладу 3.

·         Правильність виконання операцій додавання обов'язково повинна перевірятися шляхом аналізу значення виразу Р₁Å Р_2, щоб уникнути одержання некоректного результату, який виникає при переповненні розрядної сітки, при цьому: якщо Р₁ Å Р₂ = 0, одиниця в розряді переповнення ігнорується (відкидається); якщо Р₁ Å Р₂ = 1, то необхідно зсунути число на один розряд праворуч.

·         Правило перевірки коректності результату додавання двійкових чисел також можна сформулювати в такий спосіб: якщо знак операндів однаковий, а знак суми протилежний, то результат є некоректним. При додаванні двох операндів із різними знаками результат завжди коректний, якщо не брати до уваги одиницю у розряді переповнення.

Множення і ділення двійкових чисел із фіксованою комою. Множення двійкових чисел завжди виконують у прямому коді. Знак добутку визначають за знаковими розрядами множників згідно з таким загальновідомим правилом: якщо знаки операндів однакові, то знак добутку – позитивний; у протилежному випадку – знак добутку негативний.

Знак добутку двох чисел не впливає на алгоритм виконання операції множення модулів цих чисел.

Часто використовують спосіб множення, процедура якого аналогічна процедурам множення вручну. У цьому випадку результат одержують додаванням часткових добутків. Кожний частковий добуток удвічі перевищує попередній, що відповідає його зсуванню ліворуч на один розряд.

 

 

Наприклад:

1101    х  1011        1101      1101 + 0000 1101 10001111

13  х  11      13 + 13    143

 

 

 

 

 

 

Характерно, що розрядність добутку двійкових чисел удвічі перевищує розрядність співмножників. Якщо у множенні беруть участь мантиси, тобто правильні дроби, то молодші розряди, що виходять за межі розрядної сітки, можуть бути відкинуті без округлення або з округленням.

Операція ділення також виконується способом, аналогічним застосовуваному при діленні вручну, що наочно ілюструє приклад ділення двох чисел 506 : 23 = 22, тобто 0.111111010 : 0.10111 = 0.10110. Знак частки визначають аналогічно знаку добутку. Застосоване при діленні віднімання дільника виконують шляхом додавання його додаткового коду.

				0.	1	1	1	1	1	1	0	1	0	ділене додатнє
				1.	0	1	0	0	1					перше віднімання дільника
		1	1	0	0.	1	0	0	0	1				1 – результат додатній
					1.	0	1	0	0	1				– друге віднімання дільника
		0			1	1.	1	0	1	0	0			0 – від’ємний результат
						0.	1	0	1	1	1			– додавання дільника
		1			1	0	0.	1	0	1	1	1		1 – результат додатній
							1.	0	1	0	0	1		– третє віднімання дільника
		1				1	0	0.	0	0	0	0		1 – остача дорівнює нулю
		0

 

У даному прикладі використаний так званий алгоритм без відновлення остачі, що передбачає таку послідовність дій:

·    із діленого віднімається дільник (додається дільник, записаний у додатковому коді);

·    якщо остача додатня, то перша цифра частки дорівнює одиниці, у протилежному випадку – 0;

·    остача зсувається ліворуч, і до неї додається дільник із знаком, зворотним знаку остачі;

·    знак наступної остачі визначає наступну цифру частки;

·    ці дії повторюють доти, поки не утвориться необхідне число розрядів частки або нульова остача.

Слід зазначити, що оскільки даний алгоритм передбачає додавання чисел (остач і дільника) тільки з протилежними знаками, то всі розряди проміжних сум, старшим за знаковий, слід ігнорувати.

Виконання арифметичних операцій у пристроях із «плавучою» комою. Операція додавання у пристроях із «плавучою» комою відбувається у чотири етапи:

1.  Порівнюються порядки доданків: менший порядок збільшується до більшого. При цьому відповідним чином корегується мантиса числа, яке перетворюється.

2.  Виконується перетворення мантис у додаткові коди.

3. Виконується додавання мантис за правилами, розглянутими вище для чисел із фіксованою комою.

4.  До суми приписується порядок доданків і, в разі необхідності, виконується нормалізація результату.

Операція множення чисел, поданих у формі з «плавучою» комою, також виконується у чотири етапи:

1.  Визначається знак добутку.

2.  Перемножуються мантиси співмножників за правилами для чисел із фіксованою комою.

3.  Обчислюється порядок добутку алгебраїчним додаванням порядків співмножників за правилами додавання цілих чисел із знаком.

4.  Виконується нормалізація отриманого результату у випадку її необхідності.

Ділення чисел у пристроях із «плавучою» комою виконується так само, як і множення.