Тема 8. Реалізація логічних функцій у різних базах

 

5.1 Базисні набори ЛЕ і їх взаємозв’язок

Існує декілька основних (функціонально повних) наборів логічних елементів, завдяки яким можна реалізувати будь-яку перемикаючу функцію:

1) І, АБО, НІ;

2) І – НІ;

3) АБО – НІ.                                                                  

Для реалізації перемикаючої функції, представленої булевим виразом у ДНФ або КНФ, достатньо трьох ЛЕ: І, АБО, НІ, тому цей набір вважається функціонально повним або базовим (базисом).

На практиці більш широко використовуються базиси І – НІ або АБО – НІ. Це пов'язано з тим, що скорочення номенклатури елементів до одного типу спрощує проектування пристрою та його ремонту. Крім того, наявність у цих елементах інвертора (підсилювача) підвищує навантажувальну здатність елемента (підсилює сигнал).

Використовуючи тотожності і теореми булевої алгебри, можна конвертувати вираз перемикальної функції, записаної у вигляді комбінації функцій І, АБО, НІ, до вигляду, що може бути реалізований елементами базиса І – НІ, АБО – НІ. Вищесказане відображає таблиця 5.1.

 

Таблиця 5.1 – Конвертації виразів перемикальної функції

 

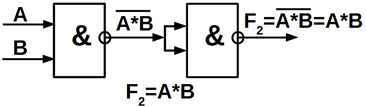
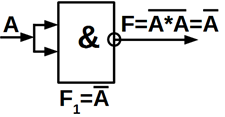
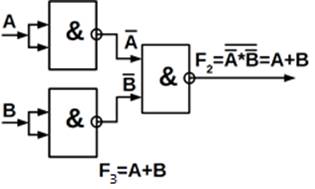
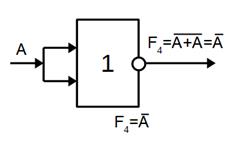
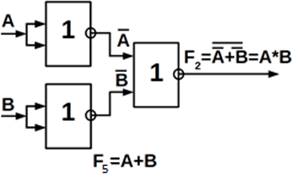
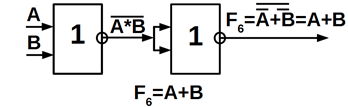
Схемну реалізацію функцій І, АБО, НІ в базисах І – НІ (рисунок 5.1, а, б, в) і АБО – НІ (рисунок 5.1 ,г, д, е), зображено нище.

Функцію І – НІ називають функцією Шеффера (штрихом Шеффера), яку позначають у вигляді F = A êB, а функцію АБО – НІ функцією Пірса (стрілкою Пірса), яку позначають її у вигляді А¯В. Базис І – НІ називають базисом Шеффера, а базис АБО-НІ – базисом Пірса.

 

               

 

a)                                                                      б)

       

в)                                                               г)

 

                д)                                                                              е)

Рисунок 5.1 – Схеми базисних функцій

 

5.2 Реалізація логічних функцій у різних базисах

5.2.1 Реалізація елемента «Рівнозначність» (виключаюче АБО – НІ)

На виході такого елемента повинна бути логічна 1-ця, якщо на входах одночасно присутні однакові логічні змінні (одиниці або нулі).

Булевий вираз логічної функції, який відповідає елементу, що розглядається, має вигляд:

 

.                                                  (5.1)

 

Очевидно, що даний вираз легко реалізується елементами базиса І, АБО, НІ. Використовуючи теорему де Моргана і тотожності булевої алгебри, перетворимо вираз (5.1) до вигляду, котрий дозволяє реалізувати функцію «рівнозначність» у базисі І – НІ (5.2) і АБО – НІ (5.3).

 

,                                                     (5.2)

.                                               (5.3)

 

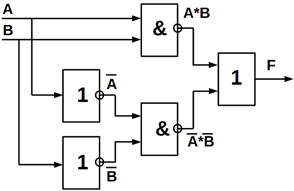
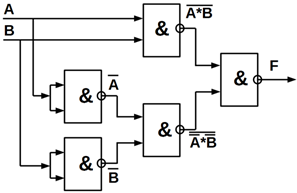
Функціональні схеми елемента «рівнозначність» на ЛЕ базисів І, АБО, НІ (рисунок 5.2, а); І – НІ (рисунок 5.2, б) і АБО – НІ (рисунок 5.2, в).

 

    

а)                                                          б)

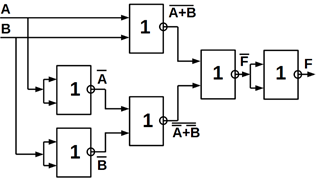
в)

Рисунок 5.2 – Функціональні схеми, що виконані з використанням базисних логічних елементів

 

5.2.2 Реалізація елемента «Нерівнозначність» (виключаюче АБО, сума по модулю два)

На виході такого елемента повинна бути логічна 1-ця, якщо на входах присутні нерівнозначні логічні змінні: F = 1, якщо А = 1, В = 0 або А = 0, В = 1.

Булевий вираз логічної функції, елемента, що розглядається, має вигляд:

 

.                                                 (5.4)

 

Цей вираз може бути легко реалізований елементами базиса І, АБО, НІ. Використовуючи теорему де Моргана і тотожності булевої алгебри, перетворимо вираз (5.4) до вигляду, котрий дозволяє реалізувати функцію «нерівнозначність» у базисі І – НІ (5.5) і АБО – НІ (5.6).

 

,                                                     (5.5)

.                                               (5.6)

 

Нижче показані функціональні схеми елемента «нерівнозначність» на ЛЕ базисів І, АБО, НІ (рисунок 5.3, а); І–НІ (рисунок 5.3, б) і АБО–НІ (рисунок 5.3, в).

Елемент «нерівнозначність» ще називають суматором за модулем два: сума двійкових цифр дає одиницю, якщо одна з них одиниця, а друга – нуль; у протилежному випадку, якщо обидві цифри 0 або 1, то сума рівна нулю.

 

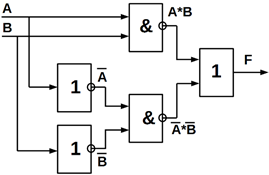
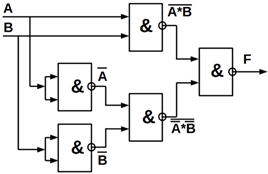
а)                                                         б)

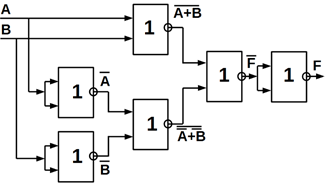
в)

Рисунок 5.3 – Функціональні схеми, які реалізують «Нерівнозначність» із використанням базисних елементів

 

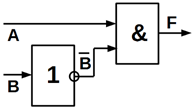
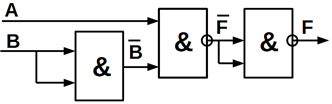
5.2.3 Реалізація елемента «Заборона»

На виході такого елемента повинна бути логічна 1-ця, якщо на основному вході присутня логічна одиниця, а на забороненому вході – логічний 0.

Булевий вираз логічної функції, елемента, що розгулядається, має вигляд:

 

.                                                               (5.7)

 

Вираз (5.7) може бути легко реалізований у базисі І, АБО, НІ.

Використовуючи теорему де Моргана і тотожності булевої алгебри, перетворимо вираз (5.7) до вигляду, котрий дозволяє реалізувати функцію «заборона» в базисі І – НІ (5.8) і АБО – НІ (5.9).

 

,                                                                (5.8)

.                                                              (5.9)

 

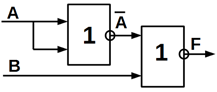
Нижче показані функціональні схеми елемента «заборона» на ЛЕ базисів І, АБО, НІ (рисунок. 5.4, а); І – НІ (рисунок. 5.4, б) і АБО – НІ (рисунок. 5.4, в).

 

                   

a)                                                           б)

в)

 

Рисунок 5.4 – Функціональна схема, яка реалізує функцію «заборона»

 

5.2.4 Реалізація багатобуквених логічних функцій на елементах із невеликою кількістю входів

Інколи на практиці виникає завдання реалізувати логічну функцію з великою кількістю логічних змінних (багатобуквену функцію) на елементах із невеликою кількістю входів. У якості прикладу на рисунку 5.5 зображено функціональну схему, яка реалізує логічну функцію:

 

,                                            (5.10)

на двовхідних елементах І – НІ.

 

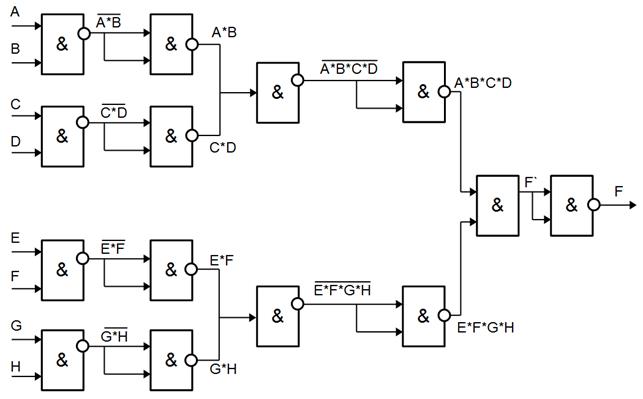
Рисунок 5.5 – Функціональна схема, які реалізує багатобуквену логічну схему