Лабораторна робота
№17-18
Тема: Двійкові коди,
що виправляють однократні помилки
Мета: вивчити визначення
штрихового коду. Його призначення. Визначити справжність товарів за допомогою
штрих коду.
Теоретичні відомості
Коди, що виправляють одну помилку, повинні мати
мінімальну кодову відстань d min ![]() 3. Збільшення кодової відстані досягається збільшенням
числа розрядів коду n при незмінній кількості
дозволених кодових комбінацій або зменшенням числа дозволених кодових
комбінацій, що використовуються для передачі повідомлень, тобто збільшенням
надмірності коду.
3. Збільшення кодової відстані досягається збільшенням
числа розрядів коду n при незмінній кількості
дозволених кодових комбінацій або зменшенням числа дозволених кодових
комбінацій, що використовуються для передачі повідомлень, тобто збільшенням
надмірності коду.
Найбільшого поширення серед двійкових кодів, що виправляють однократні помилки,
одержали систематичні
( лінійні, групові )
блокові коди: Хеммінга, ітеративний
( Елайеса ), з багатократним повторенням, інверсний, та
несистематичний код Бергера .
Систематичний код
з d min = 3, який
називають кодом Хеммінга, використовується
для виправлення однієї або виявлення двох помилок.
Систематичний ( груповий,
лінійний ) код довжиною n з кількістю інформаційних
символів k позначають
як ( n, k ) - код. Для
систематичного ( n, k ) - коду з d min = 3 кількість
перевірочних символів вибирають як найменше ціле r, що відповідає умовам
2![]()
![]() n + 1 = k + r + 1. ( 15.1 )
n + 1 = k + r + 1. ( 15.1 )
Як відомо, у систематичних кодах перевірочні
елементи можна одержати шляхом додавання
за модулем 2 визначених інформаційних елементів.
Систематичний код можна задавати твірною ( породжуваль-ною )
матрицею, якій притаманні такі особливості:
–
матриця має k
рядків та n
стовпців ;
– кожний
елемент матриці є або “0”, або “1”;
–
кожний рядок матриці являє собою кодову комбінацію коду, що
цією матрицею задається, і повинен мати не менше трьох одиниць ;
–
всі рядки матриці повинні бути лінійно незалежними ;
– поелементна
сума за модулем 2 будь - якої
кількості рядків матриці ( яка, до речі, завжди буде комбінацією
коду ) повинна мати не менше трьох одиниць.
Підібрані за даних умов вихідні комбінації, які
називають базисними, записуються у
вигляді матриці:
G n,k = ![]()
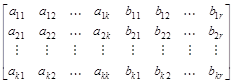 , ( 15.2)
, ( 15.2)
де a j i та b j m –
відповідно i - ий інформаційний та m - ий перевірочний елементи j - ої базисної кодової комбінацій.
Твірну матрицю ( 15.2 ) можна подати
у вигляді двох підматриць: інформаційної ( Е k )
та перевірочної ( С r, k
).
Інформаційну підматрицю зручно подати у
канонічній формі як одиничну підматрицю розміром k ![]() k:
k:
Е k =  .
.
Перевірочна
підматриця С r,k
будується підбором r - розрядних
двійкових послідовностей з числом одиниць у кожному рядку не менше за
d min – 1
= 2. При цьому необхідно
враховувати, що сума за модулем 2 будь-яких рядків цієї підматриці не повинна
мати менше за dmin – 2 = 1 одиниць, тобо однакові
набори є неприпустимими.
Рядки у перевірочній підматриці можна міняти
місцями. При цьому можна одержати декілька варіантів твірних матриць.
Твірна матриця дозволяє одержати всі кодові
комбінації систематичного групового коду. Це досягається послідовним додаванням
за модулем 2 рядків матриці у всіх можливих сполученнях
( тобто першого і другого рядків матриці; першого і третього;
першого і четвертого; . . . ; другого і третього; другого і четвертого; . . .; першого,
другого і третього; першого, другого і четвертого; . . . ,
нарешті усіх k рядків ).
Нульова комбінація дописується окремо.
Опираючись на твірну, матрицю можна побудувати перевірочну матрицю Н n,r , яка
налічує r рядків та n стовпців. Перевірочна матриця складається з
двох підматриць: підматриці D k,r , яка має k
стовпців та r рядків, кожний рядок якої відповідає
транспонованому стовпцю перевірочної підматриці
С r,k
твірної матриці G n,k , та одиничної підматриці E r розміром r ´ r :
H n,r = [ D k,r ; E r ] =  . ( 15.3 )
. ( 15.3 )
Перевірочна матриця
( 15.3 ) дозволяє спростити операції кодування і декодування.
Запишемо довільну кодову
комбінацію коду у вигляді
V = [ a1a2a3 . . . ak b1b2b3 . . . br
] ,
де a i та b m – відповідно
інформаційні та перевірочні елементи.
Позиції, які зайняті одиницями у і - ому рядку підматриці D k,r , визначають ті
інформаційні елементи, які повинні брати участь у формуванні і - ого
перевірочного елемента b i :
b1 = b11 a1 Å b21 a2 Å . . .![]() bk 1 ak ,
bk 1 ak ,
b2 = b12 a1 Å b22 a2 Å . . . Å bk 2 ak , ( 15.4 )
![]()
b r = b1r a1 Å b2 r a2 Å
. . . Å bk r ak
.![]()
Існування співвідношень ( 15.4 ), що пов’язують
інформаційні та перевірочні елементи кодової комбінації, дає можливість при
деко-дуванні виявляти та виправляти помилки в кодових комбінаціях, які можуть
з’являтися через спотворення елементів у двійковому каналі під час їх передачі.
Аналізуючи результати перевірки цих
співвідношень у прийнятій кодовій комбінації, можна отримати певну
ін-формацію про помилки.
Позначимо кодову комбінацію, яка пройшла через
двійковий канал та підлягає декодуванню,
V * = [ a![]() a
a![]() a
a![]() . . . a
. . . a![]() b
b![]() b
b![]() b
b![]() . . . b
. . . b![]() ] ,
] ,
де a![]() та b
та b![]() – відповідно інформаційні та перевірочні
елементи кодової комбінації на виході каналу.
– відповідно інформаційні та перевірочні
елементи кодової комбінації на виході каналу.
Для з’ясування питання, чи відповідає кодова
комбінація V *
правилам побудови коду, отримаємо
набір s j ,
j = 1,2,3,
. . . , r :
s j = b 1 j a![]() Å b 2 j a
Å b 2 j a![]() Å b 3 j a
Å b 3 j a![]() Å . . . Å b k j a
Å . . . Å b k j a![]() Å b
Å b![]() .
.
Кожний елемент s j дає інформацію про те,
задовольняють чи ні символи кодової кобінації
V * відповідному
рівнянню системи ( 8.4 ).
Набір
елементів ( s 1, . . . , s r )
називається кодовим синдромом або пізнавачем
помилок .
Якщо синдром складається з одних нулів, кодова
комбінація V *
є дозволеною, тобто задовольняє
правилам побудови коду.Такий результат буде мати місце, якщо в кодовій
комбінації немає помилок або конфігурація помилок є такою, що вона не може бути
виявлена цим кодом. Присутність хоча б одного ненульового елемента в комбінації
синдрому вказує на спотворення хоча б одного елемента у прийнятій кодовій
комбінації.
Значення синдрому при однократній помилці у
прийнятій кодовій комбінації збігаються із стовпцями перевірочної матриці.
Порівнюючи кодовий синдром з стовпцями матриці Н n,r ,
можна знайти місце помилки у комбінації по їх збігу. У разі помилки
виправляється той розряд кодової комбінації, який відповідає порядковому номеру
стовпця матриці, що збігається з
синдромом.
Приклади
виконання завдань
Приклад 1.
Побудувати
твірну матрицю і визначити всі комбінації двійкового систематичного
( групового ) коду, здатного виправляти поодинокі помилки для N 0 = 8 повідомлень.
Розв’язання. Кількість інформаційних розрядів коду k = log 2 8 = 3.
Кількість перевірочних розрядів визначається як найменше ціле r, яке задовольняє
нерівності 2 r = k + r + 1 ;
таким значенням буде r = 3 . Довжина коду n = k + r = 6 . Таким
чином, твірна матриця G n,k має
6 стовпців та 3 рядка, а
перевірочна підматриця C r,k має
3 стовпця та 3 рядка.
Згідно з правилом побудови підматриці C r,k
кількість одиниць у кожному рядку цієї підматриці повинно бути не менша
за d min – 1 =
= 3 – 1 = 2, а кодова відстань між окремими
рядками цієї підматриці – не менша за d min – 2 = 3 – 2 = 1.
Тому, з триелементних комбінацій для підматриці С 3,3 вибираємо тільки ті, які задовольняють цим
умовам, тобто 110, 101, 011.
За інформаційну підматрицю Е k твірної матриці обирають одиничну підматрицю.
Дописавши до неї перевірочну підматрицю, одержимо твірну матрицю систематичного
коду, здатного виправляти однократні помилки,
G 6,3 = 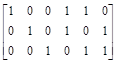 .
.
За
допомогою одержаної твірної матриці G 6,3 визначимо всі 8 кодових комбінацій,
які належать до
цього систематичного коду: 1 – 000000 ; 2 – 100110 ;
3 – 010101 ;
4 – 001011 ;
5 – 110011 ( 2 Å 3 ) ;
6 – 101101 ( 2 Å 4 ) ;
7 – 011110 ( 3 Å 4 ) ;
8 – 111000 ( 2 Å 3 Å 4 ) .
Приклад 2.
Побудувати
перевірочну матрицю двійкового систематичного коду, здатного виправляти
однократні помилки з d min = 3 .
Закодувати за допомогою одержаної перевірочної матриці комбінації первинного
двійкового коду 111 та 011.
Розв’язання. Для побудови перевірочної матриці
систематичного коду, здатного виправляти однократні помилки, скористуємось
твірною матрицею, побудованою для одержання 8 комбінацій систематичного коду
в задачі 8.2.1.
Перевірочна матриця
H n,r
повинна мати r = 3
рядки та n = 6 стовпців. Вона утворюється з двох
підматриць: D 3,3 , яка містить три
стовпці і три рядки, кожний рядок якої відповідає стовпцю пере-вірочної
підматриці С 3,3
твірної матриці G 6,3 ,
та одиничної під-матриці E 3 . Таким
чином,
Н 6,3 =  .
.
Перевірочні
елементи, згідно матриці Н 6,3 , можна
визначити так: b 1 = a 1 Å a 2 ; b 2 = a 1 Å a 3 ; b 3 = a 2 Å a 3 .
За допомогою одержаної перевірочної матриці Н 6,3 виконуємо кодування систематичним
( груповим ) кодом комбінацій первинного коду 111 та 011, для чого
визначаємо перевірочні елементи для заданих комбінацій. Для комбінації 111:
b 1 = 1 Å 1 = 0 ; b 2 = 1 Å 1 = 0 ; b 3 = 1 Å 1 = 0,
а для
комбінації 011:
b 1 = 0 Å 1 = 1 ; b 2 = 0 Å 1 = 1; b 3 = 1 Å 1 = 0.
Таким
чином, кодові комбінації систематичного ( групового ) коду будуть мати
вигляд: 111000 та
011110.
Приклад 3.
Для групового ( 7, 4 ) - коду, що виправляє
однократні помилки, побудувати перевірочну матрицю Н 7,3
і закодувати за її допомогою
комбінацію двійкового простого коду
1101, якщо твірна матриця має вигляд
G 7,4 = 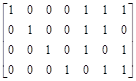 .
.
Визначити
синдром для виправлення однократних помилок в комбінаціях цього коду. Показати
на прикладі виправлення однократної помилки.
Розв’язання. Згідно
з ( 8.3 ) перевірочна
матриця Н 7,3 для ( 7, 4 ) -
коду буде складатись з
двох підматриць: D 4,3 ,
кожний рядок якої відповідає транспонованому стовпцю перевірочної
підматриці C 3,4
твірної матриці G 7,4 , та одиничної підматриці E 3 .
Отже, перевірочна матриця H 7,3 буде мати вигляд:
Н 7,3 =  .
.
Перевірочні елементи, згідно матриці Н 7,3 ,
будуть визначатись за такими виразами:
b 1 = a 1 Å a 2 Å a 3 ; b 2 = a 1 Å a 2 Å a 4 ; b 3 = a 1 Å a 3 Å a 4 .
Користуючись ними, закодуємо комбінацію [ a1 a 2 a 3 a 4 ] = = 1101,
тобто визначимо перевірочні елементи:
b 1 = 1 Å 1 Å 0 = 0 ;
b 2 = 1 Å 1 Å 1 = 1 ; b 3 = 1 Å 0 Å 1 = 0 ; таким чином,
комбінація групового коду буде
мати вигляд 1101010 .
У декодері для виявлення і виправлення однократної
помилки у прийнятій кодовій комбінації систематичного групового коду викону-
ють перевірку – визначають синдром помилки. Для одержаної пе- ревірочної матриці елементи синдрому
помилки визначаються таким чином : s 1 = a![]() Å a
Å a![]() Å a
Å a![]() Å b
Å b![]() ; s 2 = a
; s 2 = a![]() Å a
Å a![]() Å a
Å a![]() Å b
Å b![]() ; s 3 = a
; s 3 = a![]() Å a
Å a![]() Å a
Å a![]() Å b
Å b![]() .
.
Знайдемо і виправимо однократну помилку, наприклад, у
ком-бінації [ a![]() a
a![]() a
a![]() a
a![]() b
b![]() b
b![]() b
b![]() ] = 1001010.
Для цього визначимо кодовий синдром помилки: s 1 = 1 Å 0 Å 0 Å 0 = 1; s 2 = 1 Å 0 Å 1 Å
1 = 1; s 3 = 1 Å 0 Å 1 Å 0 = 0,
тобто синдром має вигляд 110, що
відповідає другому стовпцю перевірочної матриці
Н 7,3 .
Синдром показує, що помилка знаходиться у другому розряді прийнятої кодової
комбінації. Для виправлення помилки
інвертуємо значення даного розряду, тобто замість “ 0 ”
записуємо “ 1 ”. Виправлена кодова комбінація
групового коду буде мати вигляд 1101010
.
] = 1001010.
Для цього визначимо кодовий синдром помилки: s 1 = 1 Å 0 Å 0 Å 0 = 1; s 2 = 1 Å 0 Å 1 Å
1 = 1; s 3 = 1 Å 0 Å 1 Å 0 = 0,
тобто синдром має вигляд 110, що
відповідає другому стовпцю перевірочної матриці
Н 7,3 .
Синдром показує, що помилка знаходиться у другому розряді прийнятої кодової
комбінації. Для виправлення помилки
інвертуємо значення даного розряду, тобто замість “ 0 ”
записуємо “ 1 ”. Виправлена кодова комбінація
групового коду буде мати вигляд 1101010
.
Приклад 4.
Закодувати традиційним двійковим кодом Хеммінга
комбінацію двійкового простого коду
10110 і показати
на прикладі процес виправлення будь-якої однократної помилки. Визначити
надмірність коду.
Розв’язання. Згідно із
співвідношенням ( 8.1 )
при k = 5
кількість перевірочних елементів r = 4 ; довжина коду
n = k + r = 5 + 4 = 9.
Перевірочні елементи будуть розташовані на позиціях 1, 2, 4, і 8 ( див.
правила побудови перевірочної матриці коду Хеммінга ). Побудуємо
перевірочну матрицю коду Хеммінга розмірами
r = 4 рядків та
n = 9 стовпців:
Н 9,4 = 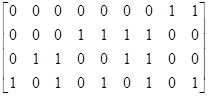 .
.
b 1 b 2 a 1 b 3
a 2 a 3 a 4 b 4
a 5
Під матрицею для полегшення процесу кодування записана
у загальному вигляді кодова
комбінація, де через a i та
b j позначені
інформаційні та перевірочні елементи
відповідно. Користуючись побудо-ваною перевірочною матрицею Н 9,4 , визначимо значення перевіроч-них
елементів для [ a1 a 2 a 3 a 4 a 5 ] = 10110 :
b 1 = a 1 Å a 2 Å a 4 Å a 5 = 1 Å 0 Å 1 Å 0 = 0 ;
b 2 = a 1 Å a 3 Å a 4 = 1 Å 1 Å 1 = 1
;
b 3 = a 2 Å a 3 Å a 4 = 0 Å 1 Å 1 = 0 ;
b 4 = a 5 = 0.
Кодова
комбінація традиційного коду Хеммінга буде мати вигляд: 011001100.
Виконаємо декодування одержаної кодової комбінації з
виправленням однократної помилки. Припустимо, що при передачі сталося
спотворення і замість 011001100 була прийнята кодова комбінація 011001000.
Для виявлення і виправлення помилки у декодері
виконують перевірки на парність з
урахуванням перевірочних елементів, тобто знаходять синдром помилки згідно
перевірочній матриці Н 9,4 :
s 1 = b 1 Å a 1 Å a 2 Å a 4 Å a 5 = 0 Å 1Å 0 Å 0 Å 0 = 1;
s 2 = b 2 Å a 1 Å a 3 Å a 4 = 1 Å 1 Å 1 Å 0 = 1;
s 3 = b 3 Å a 2 ![]() a 3 Å a 4 = 0 Å 0 Å 1 Å 0 = 1;
a 3 Å a 4 = 0 Å 0 Å 1 Å 0 = 1;
s 4 = b 4 Å a 5 = 0 Å 0 = 0.
Маємо синдром
0111. Таким чином , визначаємо, що спотворено елемент із порядковим
номером 01112 = 710 ,
тобто елемент a 4 . Виправляємо
його за допомогою інверсії та одержуємо правильну кодову комбінацію –
011001100.
Надмірність коду R = 1 – k / n = 1
– k / ( k + r ) = r / n = 4 / 9 .
Завдання на лабораторну
роботу
Завдання 1.
Побудувати
твірну матрицю двійкового систематичного ( групового ) коду, який має N0 дозволених кодових комбінацій та здатен
виправляти всі однократні помилки
( згідно з варіантом таблиці 8.3.1 ). Навести приклад кодування за допомогою твірної
матриці.
Таблиця 1
|
№ варіанта |
Кількість дозволених
комбінацій N0 |
|
1 |
8 |
|
2 |
16 |
|
3 |
32 |
|
4 |
64 |
|
5 |
128 |
Завдання 2.
Визначити,
які з наведених комбінацій двійкового групового
( 7,4 ) - коду
( згідно з варіантом таблиці
8.3.2 ), містять помилку,
якщо відомо, що код побудований за твірною матрицею:
G 7,4 =
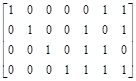 .
.
Таблиця 2
|
№ варіанта |
Комбінації двійкового
групового коду |
|
1 |
1010110,
1110010, 0001111 |
|
2 |
0101010,
1111111, 0011011 |
|
3 |
0011101,
0010110, 1101110 |
|
4 |
1100000,
1100110, 1010101 |
|
5 |
0100010,
0100101, 1001011 |
|
6 |
1110000,
0000101, 0100000 |
Завдання 3.
Визначити,
які з комбінацій двійкового групового
( 7,4 ) -коду
містять помилку ( згідно з варіантом таблиці 8.3.3 ), якщо
відомо, що перевірочна матриця коду має вигляд:
Н 7,3 =
 .
.
Таблиця 3
|
№
варіанта |
Комбінації двійкового
групвого коду |
|
1 |
0010110,
1110010, 1001111 |
|
2 |
0101110,
1111111, 1011001 |
|
3 |
1011111,
0010110, 1101110 |
|
4 |
0100011,
1100110, 0010101 |
|
5 |
0100011,
0100101, 1101011 |
Завдання 4.
Побудувати
перевірочну матрицю традиційного двійкового коду Хеммінга з заданими d min
та
k ( згідно з варіантом таблиці
8.3.4 ). За допомогою одержаної матриці закодувати кодом Хеммінга комбінації
двійкового простого коду А 1 та А 2 .
Показати на прикладі виправлення будь-якої однократної
помилки ( для коду з d min = 3 ) або виявлення будь-якої трикратної помилки
( для коду з d min = 4 ) в отриманих кодових комбінаціях коду Хеммінга
і визначити надмірність коду.
Таблиця 4
|
№ варіанта |
d min |
k |
А 1 |
А 2 |
|
1 |
3 |
4 |
0011 |
1010 |
|
2 |
3 |
5 |
11001 |
00110 |
|
3 |
3 |
7 |
0101010 |
1110000 |
|
4 |
3 |
11 |
01110001010 |
00011100011 |
|
5 |
3 |
12 |
001100110010 |
111000111000 |
|
6 |
3 |
14 |
00010001000100 |
10010010010010 |
|
7 |
4 |
4 |
1110 |
0011 |
|
8 |
4 |
7 |
0100101 |
1110001 |
|
9 |
4 |
11 |
01110111000 |
11001100111 |
|
10 |
4 |
15 |
100011100101011 |
010100010100001 |
Після
виконання завдань оформити та здати звіт викладачу.

