Лабораторна робота №7

Тема: Ентропія об’єднаних джерел

Мета: навчатися визначати ентропію об’єднання двох джерел та кількість інформації, що передається в каналі зв’язку

Теоретичні відомості

Ентропія об'єднання двох джерел інформації

Ентропію H(X, Y) об'єднання двох джерел інформації X і Y знаходять через імовірності p(x_i, y_j) системи випадкових повідомлень x_i, y_j для всіх i=1...k, і j=1...l. Для цього складається матриця ймовірностей системи двох статистично залежних джерел

 

.                              (8.1)

 

Ентропія об'єднання двох джерел H(X, Y) (взаємна ентропія) - це середня кількість інформації, що припадає на два будь-які повідомлення джерел X і Y:

 

.                              (8.2)

 

З рівності p(x_i, y_j)= p(y_j, x_i) випливає, що

H(X, Y)=H(Y, X).                        

Запишемо вираз (8.2) так:

 

      Перший доданок цього виразу відповідає безумовній ентропії H(X), а другий - умовній H(Y/X). Звідси

 

H(X, Y)=H(X)+H(Y/X).                                              (8.3)

 

Взаємної ентропії H(X, Y) має вигляд

 

H(X, Y)=H(Y)+H(X/Y),                                              (8.4)

 

звідси

     

H(Y/X)=H(X,Y)-H(X),                                              (8.5)

 

H(X/Y)=H(X,Y)-H(Y).                                              (8.6)

     

Кількість інформації, що припадає на одне повідомлення, передане по каналу зв'язку джерелом X спостерігачу Y, за наявності завад і статистичного взаємозв'язку ансамблів X і Y і властивості 4 кількості інформації і ентропії знаходиться за формулою

 

I(X,Y)=H(Y)+H(X)-H(X,Y)=H(X)-H(X/Y)=H(Y)-H(Y/X).                         (8.7)

 

Властивості ентропії об'єднання двох джерел інформації:

1)  при статистичній незалежності джерел X і Y їх взаємна ентропія дорівнює сумі ентропій кожного з джерел, тобто H(X, Y)=H(X)+H(Y);

2)  при повній статистичній залежності джерел X і Y їх взаємна ентропія дорівнює безумовній ентропії одного з джерел, тобто H(X,Y)=H(X)=H(Y);

3)  взаємна ентропія статистично залежних джерел X і Y менша суми безумовних ентропій кожного з них, тобто H(X, Y) £ H(X)+H(Y).

 

Приклади виконання завдань

Приклад_1.  Ансамблі повідомлень джерел А (А={а₁, а₂, а₃, а₄) та В (В={ b₁, b₂, b₃, b₄) поєднанні. Ймовірності сумісних повідомлень   такі:

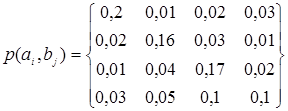
Визначити ентропію об’єднання цих джерел.

Розв'язання

Завдання на лабораторну роботу

Завдання 1

Два статистично незалежних джерела А та В визначаються матрицею сумісних ймовірностей

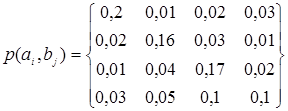
Визначити  часткову та загальну умовну ентропію, ентропію об’єднання цих джерел, а також кількість інформацій, що припадає на пару повідомлень (,).

Завдання 2

Два статистично незалежних джерела А та В визначаються матрицею сумісних ймовірностей

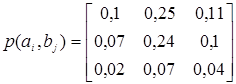
Визначити  часткову та загальну умовну ентропію, ентропію об’єднання цих джерел, а також кількість інформацій, що припадає на пару повідомлень (,).

Завдання 3

Матриця сумісних ймовірностей каналу зв'язку має вигляд

.

Знайти часткові й загальну умовні ентропії H(X/y_j), H(X/Y) і ентропію об’єднання цих джерел.

 

Після виконання завдань оформити та здати звіт викладачу.