Лабораторна робота №5-6

Тема: Умовна ентропія

Мета: навчатися визначати часткову і загальну умовну ентропію дискретного джерела повідомлень

Теоретичні відомості

Умовна ентропія

Раніше отримана формула ентропії визначає її середньою кількістю інформації, що припадає на одне повідомлення джерела статистично незалежних повідомлень. Така ентропія називається безумовною.

Як відомо з відповідного розділу математичної статистики, мірою порушення статистичної незалежності повідомлень x і у є умовна ймовірність p(x/y) появи повідомлення x_i за умови, що вже вибрано повідомлення y_j або умовна ймовірність появи повідомлення y_j, якщо вже отримане повідомлення x_i, причому в загальному випадку p(x/y)¹p(y/x).

Умовну ймовірність можна отримати з безумовної ймовірності p(x) чи p(y) та сумісної ймовірності системи в. в. p(x, y) за формулою множення ймовірностей:

 

p(x, y)=p(x)×p(y/x),

 

p(x, y)=p(y)×p(y/x),

 

звідси

,

.

В окремому випадку для статистично незалежних повідомлень маємо: p(y/x)=p(y),  p(x/y)=p(x).

При існуванні статистичної залежності між повідомленнями джерела факт вибору одного з повідомлень зменшує або збільшує ймовірності вибору інших повідомлень до умовних ймовірностей. Відповідно змінюється й кількість інформації, що міститься в кожному з цих повідомлень. Ентропія такого джерела також змінюється відповідним чином, причому обчислюється ентропія за тією самою формулою, але вже з урахуванням умовних ймовірностей. Така ентропія називається умовною.

Властивості умовної ентропії

      1)   якщо джерела повідомлень X і Y статистично незалежні, то умовна ентропія джерела X стосовно Y дорівнює безумовній ентропії джерела X і навпаки:

H(X/Y)=H(X), H(Y/X)=H(Y);

      2)   якщо джерела повідомлень X і Y настільки статистично взаємозв'язані, що виникнення одного з повідомлень спричиняє безумовну появу іншого, то їхні умовні ентропії дорівнюють нулю:

H(X/Y)=H(Y/X)=0;

3)  ентропія джерела статистично взаємозалежних повідомлень (умовна ентропія) менша від ентропії джерела незалежних повідомлень (безумовної ентропії):

H(X/Y)<H(X), H(Y/X)<H(Y).

Часткова умовна ентропія

Часткова умовна ентропія - це кількість інформації, що припадає на одне повідомлення джерела X за умови встановлення факту вибору джерелом Y повідомлення y_j, або кількість інформації, що припадає на одне повідомлення джерела Y за умови, що відомий стан джерела X:

 

 

 

де , - алфавіти повідомлень; x_i - певне повідомлення джерела X, щодо якого визначається часткова умовна ентропія H(Y/x_i) алфавіту Y за умови вибору джерелом X повідомлення x_i; y_j - певне повідомлення джерела Y, щодо якого визначається часткова умовна ентропія H(X/y_j) алфавіту X за умови вибору повідомлення y_j; i - номер повідомлення з алфавіту X; j - номер повідомлення з алфавіту Y; p(x_i/y_j), p(y_j/x_i) – умовні імовірності.            

Загальна умовна ентропія 

Визначається так:

,

.                           

Отже, загальна умовна ентропія – це середньостатистична кількість інформації (математичне сподівання), що припадає на будь-яке повідомлення джерела X, якщо відомий його статистичний взаємозв'язок з джерелом Y. Так само загальна умовна ентропія - це середня кількість інформації, яка міститься в повідомленнях джерела Y за наявності статистичного взаємозв'язку з джерелом X.

Приклади виконання завдань

Приклад_1.  Матриця умовних ймовірностей каналу зв'язку між джерелом X і спостерігачем Y має вигляд

.

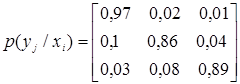      Знайти часткову та загальну умовні ентропії повідомлень у цьому каналі, якщо задано розподіл ймовірностей джерела P_x={0,65; 0,3; 0,05}.

Розв'язання

      Умовні ймовірності p(y_j/x_i) при i=j характеризують вплив завад у каналі зв'язку.

      Часткова умовна ентропія спостерігача Y щодо джерела X визначається за формулою

.

      Знайдемо часткові умовні ентропії для всіх x_i, i=1, …,3

(біт/сим);

(біт/сим);

(біт/сим).

      Знаходимо загальну умовну ентропію дискретної випадкової величини (д. в. в.) Y стосовно д. в. в. X:

(біт/сим).

 

      Скориставшись формулою множення ймовірностей

p(x_i, y_j)=p(x_i)×p(y_j/x_i),

побудуємо матрицю ймовірностей системи д. в. в. X, Y:

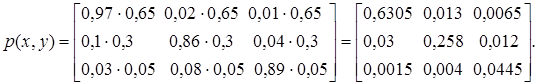Перевіряємо умову нормування: = 0,6305+0,013+0,0065+

+0,03+0,258+0,012+0,0015+0,004+0,0445=1.

      З матриці сумісних ймовірностей p(x, y) знаходимо взаємну ентропію д. в. в. X, Y:

(біт/сим).

      Скориставшись заданим рядом розподілу ймовірностей д. в. в. X, знайдемо ентропію X:

 

(біт/сим).

Перевірка: H(X, Y)=HX+H(Y/X)=1,142+0,385»1,527 (біт/сим).

      Виконавши в матриці сумісних ймовірностей p_ij= p(x, y) згортку за i, отримаємо приблизний безумовний розподіл д. в. в. Y:

;

;

.

      Перевіряємо умову нормування

            p(y₁)+ p(y₂)+ p(y₃)=0,662+0,275+0,063=1.

 

      Знаючи приблизний безумовний закон розподілу P_y={0,662; 0,275; 0,063}, знайдемо матрицю умовних ймовірностей p(x/ y), скориставшись формулою

.

      .

     

 

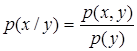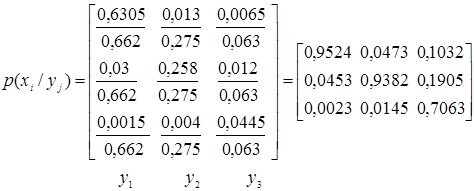Перевіряємо умови нормування:

;

;

.

      Виходячи з розподілу безумовних ймовірностей д. в. в. Y, знайдемо ентропію Y:

     

      (біт/сим).

      З матриці умовних ймовірностей p(x/ y) знайдемо часткові умовні ентропії  д. в. в. X  стосовно д. в. в. Y:

(біт/сим);

(біт/сим);

(біт/сим).

     

      Тоді загальна умовна ентропія X стосовно Y

     

(біт/сим).

      Перевірка: H(X, Y)=HY+H(X/Y)=1,157+0,369=1,527 (біт/сим).

Відповідь:  H(Y/x₁)»0,222 (біт/сим); H(Y/x₂)»0,705 (біт/сим);

H(Y/x₃)»0,593 (біт/сим); H(Y/X)»0,385 (біт/сим); H(X/y₁)»0,289 (біт/сим); H(X/y₂)»0,383 (біт/сим); H(X/y₃)»1,148 (біт/сим); H(X/Y)»0,369 (біт/сим).

 

Завдання на лабораторну роботу

Завдання 1.

Дослідження каналу зв'язку між джерелом X і спостерігачем Y виявило такі умовні ймовірності вибору повідомлень y_jÎY:

.

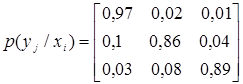Знайти часткові H(X/y_j) і загальну H(X/Y) умовні ентропії повідомлень у цьому каналі, якщо джерело задане ансамблем {x₁, x₂, x₃} з ймовірностями {0,3; 0,2; 0,5}.

 

Завдання 2.

Два статистично залежних джерела X та Y визначаються матрицею сумісних ймовірностей

.

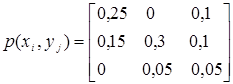Знайти часткові й загальну умовні ентропії H(X/y_j), H(X/Y) і взаємну інформацію I(X, Y).

Завдання 3.

Матриця сумісних ймовірностей каналу зв'язку має вигляд

.

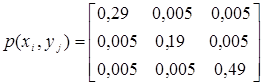Знайти часткові й загальну умовні ентропії H(X/y_j), H(X/Y) і взаємну інформацію I(X, Y).

Завдання 4

Знайти ентропії д. в. в. X, Y, Z і кількість інформації, що містить д. в. в. Z=2X+Y стосовно X та Y. X, Y – незалежні д. в. в., задані такими розподілами ймовірностей:

Завдання 5

Дискретна випадкова величина (д. в. в.) X₁ може набувати три значення: -1, 0 і 1 з однаковими ймовірностями. Д. в. в. X₂ з однаковими ймовірностями може набувати значення 0, 1 і 2. X₁ і X₂ – незалежні, Y=X₁²+X₂. Знайти кількість інформації I(X₁,Y), I(X₂,Y) і ентропії HX₁, HX₂, HY.

Завдання 6

Дискретна випадкова величина (д. в. в.) X з різною ймовірністю може набувати значень від 1 до 8. Д. в. в. Y набуває значення 0, якщо X парне, і 1, якщо X непарне. Знайти кількість інформації I(Y, X) і ентропію HX, якщо д. в. в. X задана таким розподілом ймовірностей:

 

 

Після виконання завдань оформити та здати звіт викладачу