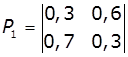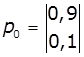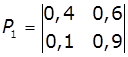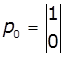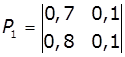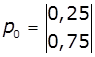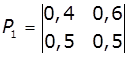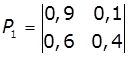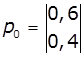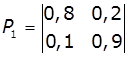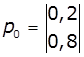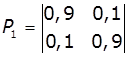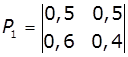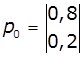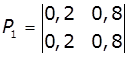Самостійна робота №9
МАРКІВСЬКІ
ДИСКРЕТНІ ПРОЦЕСИ
Мета:
Навчитись розраховувати імовірності станів Марківських
випадкових процесів.
Завдання
для самстійного розв’язання
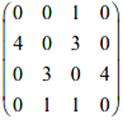
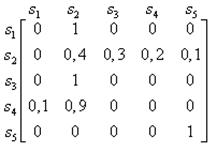
1. Задано матриці: імовірностей переходу
дискретного ланцюга Маркова Р1, та імовірностей станів в початковий
момент р0. Визначити
імовірності станів системи через k
кроків. Зобразити граф станів системи.
|
1. |
|
6. |
|
|
2. |
|
7. |
|
|
3. |
|
8. |
|
|
4. |
|
9. |
|
|
5. |
|
10. |
|
2. Матриця
переходів системи має такий вигляд
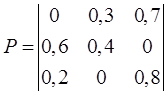
Визначити властивості цього ланцюга Маркова та
розрахувати ймовірності станів системи через три кроки, якщо початковим її
станом є другий (![]() ). Зобразити граф
станів системи.
). Зобразити граф
станів системи.
3. Задано матриці:
імовірностей
переходів дискретного ланцюга Маркова Р1 і Р2, та
імовірностей станів в початковий момент р0. Визначити імовірності станів системи після
двох кроків.
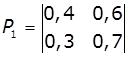 ,
, 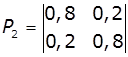
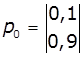
4.
Задано
матриці: імовірностей переходів дискретного ланцюга Маркова Р1, Р2
і Р3, та імовірностей станів в початковий момент р0. Визначити імовірності станів системи після
трьох кроків.
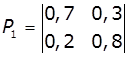 ,
, 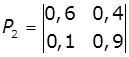 ,
, 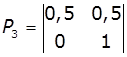
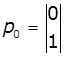
5.
Машина перевозить вантаж між чотирма пунктами, які розташовані на кільцевій
трасі. Вантажі перевозяться з кожного пункту тільки в наступний (з імовірністю 0,8)
або в попередній (з імовірністю 0,2). Початкове розташування машини – пункт 2.
Визначити ймовірності перебування машини в кожному з пунктів після трьох
перевезень, якщо матриця переходів буде мати такий вигляд:
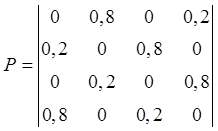
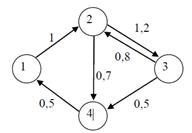
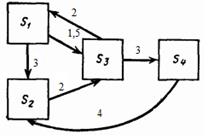
6. Граф станів і переходів системи, характерної
дискретним числом станів і неперервним часом, має вигляд, зображений на рис. 1
На дугах графа проставлено значення інтенсивності
переходів λij. Необхідно скласти систему рівнянь для визначення ймовірностей зміни
станів і розрахувати ймовірності станів системи в граничному стаціонарному
режимі.
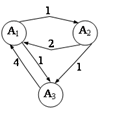
а) б) в)
г)
д)
Рис. 1. Графи станів
системи до задачі 6
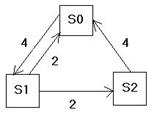
7.
Нехай агрегат складається з двох вузлів. При роботі агрегату можливі появи
наступних станів: S0 - обидва вузли справні, S1 - перший
вузол ремонтується, а другий справний, S2 - другий
вузол ремонтується, а перший справний, S3 -
два вузли в ремонті. Граф станів зображено на рис.
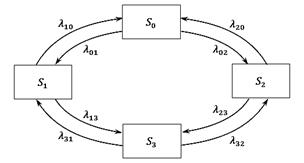
Рис. 2 Граф станів агрегату до
зад. 7.
Знайти
граничні імовірності станів агрегату при:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
1.
Задано матриці інтенсивностей переходів випадкових процесів для можливих
станів системи. Побудувати граф переходів системи, написати систему рівнянь
граничних імовірностей станів системи та знайти граничну імовірність кожного
стану.

а) б)
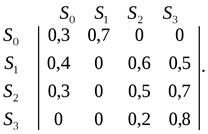
в) г)
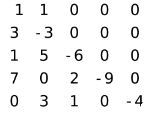 д)
д)
Приклад розв’язання задач
Ланцюгом
будемо називати послідовність випробувань, у кожному з яких може відбутися лише
одна подія з повної групи подій Q1, Q2 … Qm ... Ці події інтерпретуються як стани
системи, а чергове k-тe випробування може розглядатися
як зміна стану в момент часу tk. Процес
зміни станів ланцюга є дискретним випадковим процесом, що характеризується
дискретним часом, де pij(k) – імовірність
того, що при k-му випробуванні система перейде в стан Qj,
за умови, що під час (k – 1)-го випробування вона перебувала в стані Qi .
Послідовність
випробувань утворить ланцюг Маркова в
тому випадку, якщо ймовірність pij(k)
залежить тільки від значень i, j, k і не залежить від того, які стани мали
місце в минулому (тобто до того, як система перейшла в стан Qi),
тобто є випадковим процесом без післядії.
Ланцюг
Маркова повністю описується матрицею переходів такого вигляду:
![]()
![]()
У
кожному стовпці цієї матриці є хоча б один відмінний від нуля елемент, а
ймовірності переходу pij (k) зі
стану Qi (i = 1, m) для будь-якого
значення k (номера випробування) задовільняють таке
співвідношення:
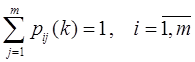
Наприклад:
матриця переходів системи має такий вигляд:
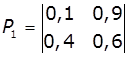 ,
, 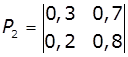
Система має два стани (m = 2). При першому випробуванні
(k = 1) ймовірність переходу зі стану Q1 до стану Q1 дорівнює 0,1 (тобто, якщо
система перебуває в стані Q1, то при першому випробуванні з імовірністю 0,1
вона в ньому залишиться). Імовірність переходу із стану Q1 в стан Q2 дорівнює
0,9 (тобто з ймовірністю 0,9 система перейде зі стану Q1 в стан Q2). Аналогічно
ймовірність переходу при першому випробуванні із стану Q2 до Q1 дорівнює 0,4, а
з Q2 в Q2 – 0,6. Матриця P2 описує поведінку
системи в другому випробуванні. Граф
станів системи має вигляд:
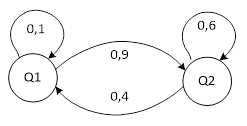 ,
, 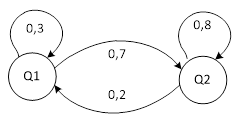
Рис.3. Графи станів для двох
випробувань
Ланцюг
Маркова називається скінченним, якщо
він характеризується скінченною множиною станів.
Ланцюг
Маркова називається незвідним, якщо кожен
стан системи може бути отриманий із будь-якого іншого стану.
Ланцюг
Маркова називається періодичним, якщо
повернення системи в будь-який стан відбувається тільки через певну кількість
кроків, кратну деякому цілому числу γ, більшому за 1 (γ > 1).
Характерним
випадком ланцюга Маркова є однорідний
ланцюг, у якому перехідні ймовірності pij (k) не
залежать від номера випробування k, тобто pij(k)
= pij .
Стовпець
ймовірностей того, що при n-му випробуванні система перейде відповідно в стани
Q1, Q2 … Qm , можна визначити таким чином:
![]()
де
р(0) – стовпець початкових імовірностей станів системи, Р’ – транспонована матриця;
![]() .
.
Приклад 1.
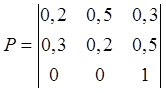
Визначити властивості цього ланцюга Маркова та розрахувати
ймовірності станів системи через три кроки, якщо початковим її станом є перший.
Розв’язування
Цей ланцюг скінченний (кількість станів – три), звідний
(оскільки із стану 3 не можна перейти в жоден інший), неперіодичний, однорідний
(матриця переходу не залежить від номера випробування).
Для однорідного ланцюга вектор імовірностей станів
визначається за такою формулою:
![]()
де n – кількість кроків; p(0) – вектор
початкових станів; p(n) – вектор станів через n кроків; P
– матриця переходів.
Виконаємо
обчислення, якщо n = 3, тоді:
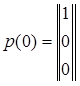 ,
, 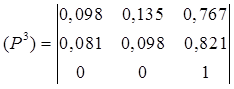 ,
,
Тоді
транспонована матриця:
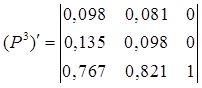 ,
,
Остаточно:
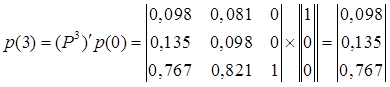
Отже ймовірності станів системи через три кроки
становлять: першого – р1(3)=0,098 другого – р2(3)=0,135 і третього –
р3(3)=0,767.
Із збільшенням числа випробувань
n система наближається до свого граничного стану. З практичного погляду цікавим є визначення
ймовірностей станів системи саме в граничному стаціонарному режимі. Для їхнього
розрахунку використовується система алгебраїчних рівнянь:
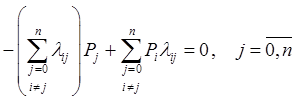 .
.
Система лінійно залежна, тому її необхідно доповнити
рівнянням:
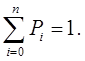
Таким чином, для опису поведінки Марківських дискретних процесів, з неперервним часом,
необхідно:
1. Ввести поняття стану системи.
2. Визначити всі стани, у яких може
перебувати система.
3. Скласти граф станів і переходів
системи, тобто окреслити шляхи можливих безпосередніх переходів системи з
одного стану в інший.
4. Для розрахунку перехідних процесів у
системі визначити, у якому стані вона перебуває в початковий момент часу.
5. Для кожного можливого переходу на
графі показати інтенсивність λij потоку
подій, що переводять систему зі стану Хi в
стан Хj. Інтенсивності λij,
як правило, визначаються експериментально.
Приклад
2.
Два абоненти А і В працюють
із одним інформаційним центром. У кожен момент часу центр може обслуговувати
тільки одного абонента. Абонент А має більш високий пріоритет, тому,
якщо від А приходить заявка, то обслуговування абонента В припиняється
до закінчення обслуговування абонента А. За таких умов потрібно:
1. Розрахувати ймовірності можливих
станів даної системи, коли відомі інтенсивності потоків подій, що переводять
систему в сусідні стани.
2. З'ясувати, чи буде система працювати
ефективно, коли відомо, що для цього необхідно, аби втрати часу абонента В на
очікування становили б не більше 50 % часу його обслуговування.
3. Встановити, які параметри і яким
чином повинні змінитися, щоб підвищилася ефективність обслуговування абонента В?
Розв’язання
Уведемо поняття стану системи.
Очевидно, що стан системи визначається
станом абонентів А і В. Для абонента А можливі два стани:
0 – відсутність заявки; 1 – обслуговування. Для абонента В можливі три
стани: 0 – відсутність заявки; 1 – обслуговування; 2 – очікування
обслуговування. Тоді можна визначити такі стани системи:
(0, 0) – X1 – відсутність заявок
від абонентів А і В;
(0, 1) – X2 – відсутність заявки
від абонента А й обслуговування абонента В;
(1, 0) – X3 – обслуговування
абонента А і відсутність заявки від абонента В;
(1, 2) – X4 – обслуговування
абонента А й очікування обслуговування для абонента В.
Граф станів і переходів системи має
вигляд, який зображено на рис.4.
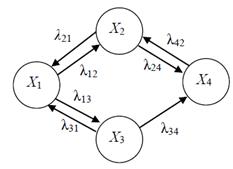
Рис.4 Граф станів і переходи системи.
Складемо систему алгебраїчних рівнянь
для визначення ймовірностей станів:
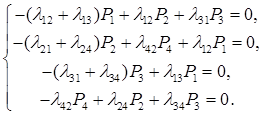
Крім того це система лінійно залежних
рівнянь. Тому одне з рівнянь (не важливо, яке) необхідно замінити умовою ![]() . Замінимо нею перше рівняння системи.
. Замінимо нею перше рівняння системи.
Допустимо, що для графа задано такі
значення інтенсивності:
![]()
![]()
![]()
![]()
![]()
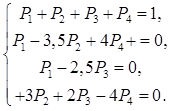
Розв’язуючи систему, одержимо, що
![]()
![]()
![]()
![]()
Відношення часу очікування й часу
обслуговування абонента В визначається відношенням імовірностей станів Р4
і Р2, тобто:
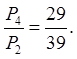
Оскільки це відношення більше 0,5 (50
%), то можна зробити висновок про неефективність роботи системи.
Приклад
3.
В умовах попередньої задачі скласти граф
станів і переходів для визначення ймовірностей станів системи, якщо з
інформаційним центром працює три абоненти А, В, С, а їхні
пріоритети мають вигляд A > B > C.
Уведемо такі позначення:
0 – відсутність заявки,
1 – обслуговування,
2 – очікування обслуговування.
Тоді можливі стани системи можуть бути
описані таким чином:
X1 – (0, 0, 0) – відсутність заявок від абонентів А,
В, С;
X2 – (1,0,0) – обслуговування абонента А,
відсутність заявок від абонентів В, С;
X3 – (0,1,0) – обслуговування абонента В,
відсутність заявок від абонентів А, С;
X4 – (0,0,1) – обслуговування абонента С,
відсутність заявок від абонентів А, В;
X5 – (1,2,0) – обслуговування абонента А,
очікування обслуговування для абонента В, відсутність заявок від
абонента С;
X6 – (1,0,2) – обслуговування абонента А,
відсутність заявок від абонента В, очікування для абонента С;
X7 – (0,1,2) – відсутність заявок від абонента А,
обслуговування В, очікування обслуговування для абонента С;
X8 – (1,2,2) – обслуговування абонента А ,
очікування обслуговування для абонентів В, С.
Граф
станів і переходів системи має вигляд, зображений на рис.5.
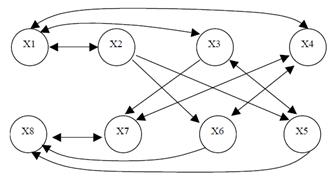
Рис . 5
Граф станів і переходи системи
Приклад
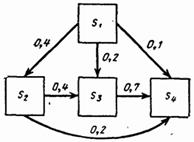
4.
Три рибальських траулери обслуговує одна
плавуча база. Середній час плавання траулера становить 2 доби, після чого він
прибуває на базу для обслуговування. На базі є один причал, а середній час
обслуговування траулера дорівнює 8 годин. Визначити середній час простою бази,
вважаючи, що процеси в цій системі Марківські.
Розв’язання
Цей об'єкт можна описати як систему
масового обслуговування із скінченним числом вимог. Уведемо поняття станів
системи:
– на базі немає жодного траулера
(простій бази); 0 X
– на базі обслуговується один траулер; 1
X
– один траулер обслуговується, а ще один
– у черзі; 2 X
– один траулер обслуговується, а два – у
черзі. 3 X
Граф станів і переходів системи
зображено на рис.:

Визначимо інтенсивності μ і λ
потоків обслуговування і вимог відповідно, враховуючи, що вони повинні мати
однакову розмірність, а саме:
λ=0,5 доби-1
, μ=3 доби-1.
Граничні ймовірності станів Рj, j=0,..3, обчислимо, розв’язуючи таку систему рівнянь:


Контрольні
запитання
1. Які
процеси називаються Марківськими?
2. Що
можна зобразити на графі станів системи?
3. Як
складається матриця імовірностей переходів?
4. Однорідний
та неоднорідний ланцюг маркова. Навести приклад.
5. Що
таке інтенсивність потоку обслуговування?
6. Що
таке інтенсивність потоку вимог (заявок)?
7. Що
означає гранична імовірність станів?