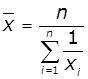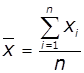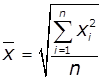Самостійна робота №3
оцінка параметрів системи при різних типах групування
даних
Мета.
Навчитись порівнювати сукупності оцінок параметрів системи при різних типах
групування даних.
Завдання
для самостійного розв’язання
1.
Розділити групу студентів на підгрупи по 5 чоловік, кожна підгрупа вибирає
певний вид продукції в асортименті 5 - 8 широковідомих марок і проводить їх
незалежну оцінку кожним із членів підгрупи (виставляє оцінку кожному виду
продукції). Заповнити таблицю і отримати
ранжований ряд видів продукції для кожної підгрупи.
|
Об’єкт oцінки |
Респонденти (кількість
студентів в групі) |
Сер.
арифм. оцінок |
Ранг по середн. оцінці |
Мода |
Медіана |
Ранг по методу медіан |
|||
|
1 |
2 |
… |
N |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||
|
П1 |
|
|
|
|
|
|
|
|
|
|
П2 |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
Пm |
|
|
|
|
|
|
|
|
|
2. Для заданих дискретних рядів визначити
величини основних середніх: гармонічне, геометричне, арифметичне, квадратичне.
|
№\хі |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
4,6 |
6,1 |
5,1 |
5,9 |
2,4 |
4,0 |
5,5 |
2,3 |
8,1 |
7,8 |
|
2 |
33 |
40 |
35 |
39 |
22 |
30 |
37 |
22 |
51 |
49 |
|
3 |
26 |
41 |
31 |
39 |
4 |
20 |
35 |
3 |
61 |
58 |
|
4 |
1289 |
2042 |
1546 |
1946 |
192 |
1029 |
1739 |
179 |
3079 |
2924 |
|
5 |
38 |
65 |
59 |
6 |
-11 |
63 |
35 |
-19 |
21 |
56 |
|
6 |
6,6 |
8 |
7 |
7,9 |
4,4 |
6 |
7,4 |
4,4 |
10,2 |
9,9 |
|
7 |
66 |
69 |
68,5 |
64 |
50 |
61 |
67 |
52 |
65 |
67 |
|
8 |
80 |
88 |
78 |
81 |
77 |
89 |
88,5 |
85 |
86 |
70 |
|
9 |
9 |
9,5 |
9,1 |
8,9 |
8,5 |
10 |
9,9 |
9,9 |
10,2 |
9,5 |
|
10 |
100 |
112 |
220 |
150 |
66 |
78 |
144 |
111 |
30 |
1 |
3.
Для випадкового набору даних (не менше
50) сформувати інтервальний варіаційний ряд.
Розрахувати моду і медіану для інтервального ряду за означенням і
використовуючи засоби MS Excel.
Приклад виконання завдання
Оцінити середні значення для різних типів варіаційних
даних.
1. Для ранжованих рядів.
Розглянемо
обробку думок експертів, виміряних в порядковій шкалі. Кожен з 5 експертів
виставляє оцінку кожному з об'єктів експертизи від 1 до n (наприклад, одному з
варіантів стратегічного розвитку фірми, якості продукту П, тощо), колонка 2
таблиці 1. Метою дослідження є отримання ранжованого ряду видів продукції чи
послуг з рангами від 1 – найкращий продукт, до 8 - найгірший, що може бути
основою для прийняття рішень про збільшення/зменшення об’ємів виготовлення
продукції, проведення реклами, тощо.
Таблиця 1
|
Об’єкт оцінки |
Експерти
(респонденти) |
Сер.
арифм. оцінок |
Ранг по середн.оцінці |
Мода |
Медіана |
Ранг по методу медіан |
||||
|
1 |
2 |
3 |
4 |
5 |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||||
|
П1 |
8 |
5 |
6 |
4 |
6 |
5,8 |
6 |
6 |
6 |
5,5 |
|
П2 |
1 |
6 |
2 |
8 |
7 |
4,8 |
5 |
- |
6 |
5,5 |
|
П3 |
7 |
1 |
3 |
1 |
1 |
2,6 |
2 |
1 |
1 |
1 |
|
П4 |
6 |
4 |
4 |
2 |
2 |
3,6 |
3 |
2
і 4 |
4 |
3,5 |
|
П5 |
2 |
3 |
1 |
3 |
3 |
2,4 |
1 |
3 |
3 |
2 |
|
П6 |
3 |
2 |
5 |
5 |
4 |
3,8 |
4 |
5 |
4 |
3,5 |
|
П7 |
5 |
8 |
8 |
6 |
8 |
7 |
8 |
8 |
8 |
8 |
|
П8 |
4 |
7 |
7 |
7 |
5 |
6 |
7 |
7 |
7 |
7 |
Якщо
обрахувати середнє арифметичне рангів кожного рядка, то можна впорядкувати
продукти в порядку зростання середнього значення (колонки 3 і 4). При
детальнішому аналізі видно, на результат ранжування вплинула значна розбіжність
думок експертів щодо продуктів П3, П4, П5, це показує недолік використання
середньоарифметичних значень в порядкових шкалах. Для порядкової шкали оцінкою
може служити обчислення медіани і моди оцінок експертів.
Мода показує який показник зустрічається найчастіше в
розподілі продукту по місцях (колонка 5). Для обчислення медіани (колонка 7)
впорядковуємо по зростанню кожен рядок і знаходимо значення, що стоїть в
середині ряду (наприклад перший – 4,5,6,6,8 медіана – 6 – половина респондентів
поставили продукт на місце менше 6, а друга половина – більше 6). Впорядковуємо
продукти в порядку зростання медіан (колонка 7).
Розглянутий приклад демонструє схожість і відмінність ранжувань,
отриманих за методом середніх арифметичних рангів і по методу медіан, а також
користь від їх спільного застосування.
2. Для дискретних рядів.
Нехай
деякий параметр системи заданий множиною дискретних значень. Необхідно
охарактеризувати ряд по його середніх величинах. Вибір середньої величини в
загальному здійснюється в залежності від умов реальної задачі.
Використання
середнього арифметичного ґрунтується
на припущенні, що вихідна величина розподілена нормально - всі можливі значення
сконцентровані біля деякого найбільш частого значення а відхилення в більшу і
меншу сторону відносно невеликі. Реально такий розподіл зустрічається рідко.
Тривалість
обслуговування абонентів, час очікування, сума контракту, розмір переведення,
частка ринку, відсоток приросту - всі ці і багато інших показників розподілено
ненормально, і їх, як правило, не варто усереднювати за допомогою середнього
арифметичного. Нормальний розподіл зазвичай зустрічається при великому числі
значень - сотні і тисячі штук. Наприклад, число звернень в крупний колл-центр
може бути розподілене нормально і тому в кожному випадку слід переконатися в
нормальності розподілу.
Значення
середнього гармонійного
застосовується тоді, коли необхідно, щоб при усередненні незмінною залишалась
сума величин обернених усереднюваним, найчастіше коли параметри ряду зв’язані з
часом і продуктивністю.
Наприклад: працівник А виконує операцію за 10
хв, а працівник Б – за 25. За скільки часу вони разом виконають операцію.
Відповідь – 14 хв 17 сек (на відміну від середнього арифметичного 17 хв 30
сек), що дозволяє визначити темп надходження заявок на обслуговування.
Перші
100 км шляху автомобіль проїхав зі швидкістю 50 км/год, другі 100км – 80
км/год. Тоді середня швидкість його руху – за середнім гармонійним – 61,54 км/год
– така, при якій на ту ж дорогу затрачається той же час.
Середнє геометричне
застосовується тоді, коли значення параметра виражають відносні величини
динаміки, побудовані в вигляді ланцюжкових величин, як відношення кожного
наступного члена ряду до попереднього, найчастіше зустрічається в
бізнес-задачах з відсотками і долями, якщо в задачі якість показники змінюються
(ростуть чи падають).
Наприклад:
в 2015 році прибуток виріс на 12% від попереднього року, в 2016 – на 42%. На
скільки в середньому виріс прибуток ![]() =26,11%.
=26,11%.
Середнє квадратичне
обраховується для обчислення середньої величини сторін n квадратних ділянок,
середніх діаметрів труб, значень напруги і сили змінного струму – для
обчислення яких використовується квадратична функція.
Таблиця 2
|
Вид
середнього |
гармонічне |
геометричне |
арифметичне |
квадратичне |
|
Показник
степеня |
-1 |
1 |
0 |
2 |
|
Формула |
|
|
|
|
3. Для інтервальних рядів.
Якщо
не задано інакшого, то для побудови інтервального ряду необхідно вибрати
оптимальне число груп (інтервалів ряду) і встановити довжину інтервалу.
Величина одного інтервалу ряду визначається як відношення розмаху варіації R (різниця між найбільшим і найменшим
значенням) до кількості груп даних m: ![]() ,
,
де
![]() ,
, ![]() ,
, ![]() - число одиниць
сукупності.
- число одиниць
сукупності.
Використовуючи
MS Excel (див. рис. 1) необхідно
здійснити наступні розрахунки:
-
згенерувати дискретний ряд цілих чисел
(кількість не менше 50) в діапазоні від 0 до 1000 використовуючи функцію СЛЧИС() (повертає випадкове число в
діапазоні від 0 до 1):
Xi=1000*
СЛЧИС();
-
визначити розмах ряду R, кількість інтервалів m і ширину інтервалу h;
-
записати межі інтервалів ( [X0; X0+h), [X0+h;
X0+2h), [X0+2h; X0+3h)…);
-
підрахувати кількість попадань чисел ряду в
кожен інтервал f.
Для
цього використаємо функцію ЧАСТОТА:
Wj=ЧАСТОТА (масив
даних; масив інтервалів)
- обраховує накопичену частоту появи значень
в інтервалі від X0 до X0+j*h .
Якщо після запису цієї функції виділити комірки значень
частот f1..f7 натиснути F2 а потім клавіші CTRL
+ SHIFT +ENTER
отримаємо формулу в вигляді масиву частот даних по окремих інтервалах:
f j ={=ЧАСТОТА (масив
даних; масив інтервалів)}
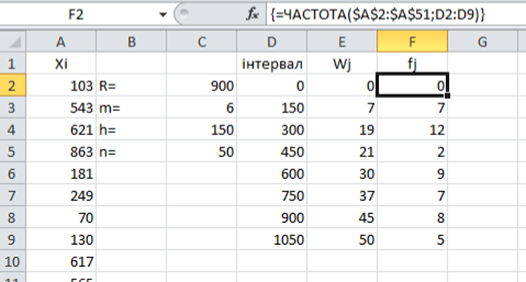
Рис. 1. Побудова інтервального
ряду.
Наприклад табл. 3
- інтервальний варіаційний ряд розподілу користувачів послуг певного підприємства
в залежності від їх віку.
Таблиця 3
|
Вікові групи інтервал |
Число користувачів fi |
Сума накопичених частот
wi |
|
До 20 р |
346 |
346 |
|
20 — 25 |
872 |
1218 |
|
25-30 |
1054 |
2272 |
|
30 — 35 |
781 |
3053 |
|
35 — 40 |
212 |
3265 |
|
40 — 45 |
121 |
3386 |
|
> 45 р |
76 |
3462 |
|
Всього |
3462 |
|
Мода — це варіант ряду, що найбільш часто зустрічається. Модою
для дискретного ряду є варіант, з найбільшою частотою. При обчисленні
інтервального варіаційного ряду необхідно спочатку визначити модальний інтервал
(по максимальній частоті), а потім — значення модальної величини ознаки по
формулі:
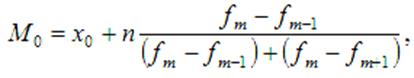
де: ![]() — значення моди,
— значення моди, ![]() — нижня межа
модального інтервалу,
— нижня межа
модального інтервалу, ![]() — величина інтервалу,
— величина інтервалу, ![]() ,
, ![]() ,
, ![]() — частота модального інтервалу, інтервалу перед ним і
наступного за модальним.
— частота модального інтервалу, інтервалу перед ним і
наступного за модальним.
Медіана — це значення ознаки, яке ділить цей
ряд на дві рівні за чисельністю частини. Для визначення медіани в дискретному
ряді за наявності частот спочатку обчислюють напівсуму частот ![]() , а потім визначають, яке значення варіанту доводиться на
неї. (Якщо відсортований ряд містить непарне число ознак, то номер медіани
обчислюють за формулою: Ме = (n + 1)/2,
n - число ознак в сукупності. В
випадку парного числа ознак медіана рівна середньому з двох центральних ознак.
, а потім визначають, яке значення варіанту доводиться на
неї. (Якщо відсортований ряд містить непарне число ознак, то номер медіани
обчислюють за формулою: Ме = (n + 1)/2,
n - число ознак в сукупності. В
випадку парного числа ознак медіана рівна середньому з двох центральних ознак.
При обчисленні медіани для інтервального варіаційного
ряду спочатку визначають медіанний інтервал, в межах якого знаходиться медіана,
а потім — значення медіани по формулі:
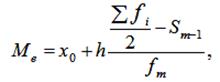
де: ![]() — шукана медіана,
— шукана медіана, ![]() — нижня межа інтервалу, який містить медіану,
— нижня межа інтервалу, який містить медіану, ![]() — величина інтервалу,
— величина інтервалу, ![]() — сума частот або
число членів ряду,
— сума частот або
число членів ряду, ![]() - сума накопичених
частот інтервалів, передуючих медіанному,
- сума накопичених
частот інтервалів, передуючих медіанному, ![]() — частота медіанного інтервалу.
— частота медіанного інтервалу.
Для табл.3. модальний інтервал знаходиться в межах
вікової групи 25-30 років (частота - 1054). Розрахуємо величину моди:
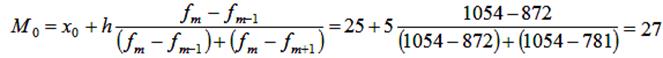
Це означає що
модальний вік користувачів дорівнює 27 рокам.
Обчислимо медіану.
Медіанний інтервал знаходиться у віковій групі 25-30 років, оскільки в межах
цього інтервалу розташована варіанту, яка ділить сукупність на дві рівні
частини (Σfi/2 = 3462/2 = 1731). Тоді:
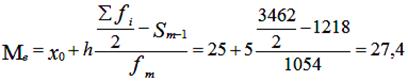
Це означає що одна половина користувачів має вік до 27,4
років, а інша понад 27,4 років.
Знаходимо моду і медіану ряду використовуючи функції MS Excel МОДА.ОДН (масив даних) та МЕДИАНА(масив даних).
Контрольні запитання
1.Пояснити
різницю між поняттями: атрибутивний, варіаційний, ранжований ряд.
2.Пояснити
різницю між поняттями дискретний і інтервальний ряд.
3.Як
сформувати інтервальний ряд даних?
4.Що таке мода? Обчислення моди для інтервального і дискретного
рядів.
5.Що таке медіана? Обчислення медіани для інтервального і
дискретного рядів.
6.Пояснити
різницю в визначення і застосуванні наступних видів середнього: середнє
арифметичне, середнє квадратичне, середнє геометричне, середнє гармонійне.