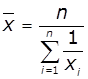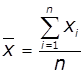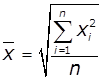4.3. Оцінка середніх величин.

Як порівнювати сукупності даних, виражених в різних шкалах чи згрупованих по різних ознаках? Очевидно, найпростіший спосіб – по середніх значеннях.

Відомі різні види середніх величин: середнє арифметичне, медіана, мода, середнє геометричне, середнє гармонійне, середнє квадратичне.

Узагальненням декількох з перерахованих є середнє по Колмогорову. Для чисел середнє по Колмогорову обчислюється за формулою:

G{F(X₁)+F(X₂)+…+F(Xn))/n},

де F – строго монотонна функція, G – функція, зворотна до F. Серед середніх по Колмогорову, багато добре відомих функцій.

Так, якщо F(x) = x, то середнє по Колмогорову – це середнє арифметичне, якщо F(x) = ln x, то середнє геометричне, якщо F(x) = 1/x, то середнє гармонійне, якщо F(x) = x², то середнє квадратичне, і так далі.

Нехай деякий параметр системи заданий множиною дискретних значень. Необхідно охарактеризувати ряд по його середніх величинах. Вибір середньої величини в загальному здійснюється в залежності від умов реальної задачі.

Використання середнього арифметичного ґрунтується на припущенні, що вихідна величина розподілена нормально - всі можливі значення сконцентровані біля деякого найбільш частого значення а відхилення в більшу і меншу сторону відносно невеликі. Реально такий розподіл зустрічається рідко.

Тривалість обслуговування абонентів, час очікування, сума контракту, розмір переведення, частка ринку, відсоток приросту - всі ці і багато інших показників розподілено ненормально, і їх, як правило, не варто усереднювати за допомогою середнього арифметичного. Нормальний розподіл зазвичай зустрічається при великому числі значень - сотні і тисячі штук. Наприклад, число звернень в крупний колл-центр може бути розподілене нормально і тому в кожному випадку слід переконатися в нормальності розподілу.

Значення середнього гармонійного застосовується тоді, коли необхідно, щоб при усередненні незмінною залишалась сума величин обернених усереднюваним, найчастіше коли параметри ряду зв’язані з часом і продуктивністю.

Наприклад: працівник А виконує операцію за 10 хв, а працівник Б – за 25. За скільки часу вони разом виконають операцію. Відповідь – 14 хв 17 сек (на відміну від середнього арифметичного 17 хв 30 сек), що дозволяє визначити темп надходження заявок на обслуговування.

Перші 100 км шляху автомобіль проїхав зі швидкістю 50 км/год, другі 100км – 80 км/год. Тоді середня швидкість його руху – за середнім гармонійним – 61,54 км/год – така, при якій на ту ж дорогу затрачається той же час.

Середнє геометричне застосовується тоді, коли значення параметра виражають відносні величини динаміки, побудовані в вигляді ланцюжкових величин, як відношення кожного наступного члена ряду до попереднього, найчастіше зустрічається в бізнес-задачах з відсотками і долями, якщо в задачі якість показники змінюються (ростуть чи падають).

Наприклад: в 2015 році прибуток виріс на 12% від попереднього року, в 2016 – на 42%. На скільки в середньому виріс прибуток =26,11%.

Середнє квадратичне обраховується для обчислення середньої величини сторін n квадратних ділянок, середніх діаметрів труб, значень напруги і сили змінного струму – для обчислення яких використовується квадратична функція.

Таблиця 2

Вид середнього	гармонічне	геометричне	арифметичне	Квадратичне
Показник степеня	-1	1	0	2
Формула

З іншого боку, такі популярні середні, як медіана і мода, не можна представити у вигляді середніх по Колмогорову.

Мода – це варіант ряду, що найбільш часто зустрічається. Мода застосовується, наприклад, при визначенні параметрів товару, що має найбільший попит у покупців. Модою для дискретного ряду є варіант, з найбільшою частотою. При обчисленні інтервального варіаційного ряду необхідно спочатку визначити модальний інтервал (по максимальній частоті), а потім – значення модальної величини ознаки по формулі:

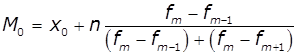
де: – значення моди, – нижня межа модального інтервалу, – величина інтервалу, , , – частота модального інтервалу, інтервалу перед ним і наступного за модальним.

Медіана – це значення ознаки, яке ділить цей ряд на дві рівні за чисельністю частини. Для визначення медіани в дискретному ряді за наявності частот спочатку обчислюють напівсуму частот , а потім визначають, яке значення варіанту доводиться на неї. (Якщо відсортований ряд містить непарне число ознак, то номер медіани обчислюють за формулою: Ме = (n + 1)/2, n - число ознак в сукупності. В випадку парного числа ознак медіана рівна середньому з двох центральних ознак.

При обчисленні медіани для інтервального варіаційного ряду спочатку визначають медіанний інтервал, в межах якого знаходиться медіана, а потім – значення медіани по формулі:

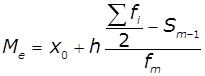
де: – шукана медіана, – нижня межа інтервалу, який містить медіану, – величина інтервалу, – сума частот або число членів ряду, – сума накопичених частот інтервалів, передуючих медіанному, – частота медіанного інтервалу.

Опишемо види допустимих середніх в основних шкалах:

- в шкалі найменувань в якості середнього годиться тільки мода;

- в порядковій шкалі в якості середніх можна використовувати тільки члени варіаційного ряду (порядкові статистики), зокрема, медіану, але не середнє арифметичне, середнє геометричне і так далі;

- у шкалах інтервалів можна застосовувати тільки середнє арифметичне;

- у шкалі відношень стійкими відносно порівняння є тільки степеневі середні і середнє геометричне.