4.1 Загальні положення

 

Загальне завдання оптимізації полягає у пошуку екстремуму цільової функції:

                                     (4.1)

при n змінних, при m обмеженнях, заданих у формі рівностей і (або) нерівностей:

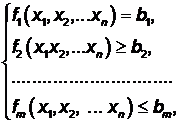                                       (4.2)

і граничних умовах, що задають діапазон зміни змінних:

d_iх_iD_i,  i=0,1,2,...n.                                        (4.3)

Якщо в математичній моделі оптимізаційної задачі є нелінійні залежності, для розв’язування цієї задачі використовуються методи нелінійного програмування.

Більшість реальних оптимізаційних завдань є нелінійними.

Як відзначалося в п. 1.2. нелінійна цільова функція може мати один або кілька екстремумів. Існуючі методи нелінійного програмування дозволяють знайти один екстремум цільової функції і не дають відповіді на питання: чи є цей екстремум локальним або глобальним?

Тому при багатоекстремальній цільовій функції діапазон зміни змінних (4.3) розбивається на ряд більш вузьких діапазонів, наприклад:

, , ,                 (4.4)

у кожному з яких шукається локальний екстремум цільової функції. З отриманих локальних екстремумів вибирається глобальний екстремум. Для випадку (4.4) оптимізаційна задача розв’язується тричі: в діапазоні зміни змінних d_iх_ia_i, у діапазоні a_iх_ib_i і в діапазоні b_iх_iD_i. У результаті одержуємо три локальних екстремуми. Із трьох локальних екстремумів вибирається глобальний екстремум.

Найбільш простими задачами нелінійного програмування є задача безумовної оптимізації. У цих задачах шукається абсолютний екстремум цільової функції без обмежень і граничних умов.

З курсу вищої математики відомо, що в точці екстремуму (мінімуму, максимуму) нелінійної функції всі її часткові похідні дорівнюють нулю. Отже, для знаходження екстремуму нелінійної функції n змінних необхідно визначити її часткові похідні за всіма змінними і прирівняти їх до нуля. Розв’язок отриманої системи n рівнянь з n невідомими дасть значення змінних, при яких досягається екстремум функції.

Слід зазначити, що точний розв’язок системи рівнянь, в загальному випадку системи нелінійних рівнянь, являє собою досить складне завдання. Тому для відшукання екстремуму нелінійної функції часто використовуються інші методи, зокрема градієнтні методи.

Задачі безумовної мінімізації на практиці зустрічаються рідко, однак методи їхнього розв’язку є основою розв’язку більшості практичних задач умовної оптимізації. У цих задачах шукається умовний екстремум цільової функції, тобто екстремум функції при наявності обмежень і граничних умов.

У більшості практичних оптимізаційних задачах шукані змінні приймають тільки додатні або нульові значення. У цьому випадку граничні умови мають вигляд:

,                                    (4.5)

Нижче будуть розглядатися задачі безумовної й умовної оптимізації, у яких шукається один екстремум цільової функції при граничних умовах виду (4.5).