ЛАБОРАТОРНА РОБОТА 4

ВИЗНАЧЕННЯ КРИТИЧНОЇ ЧАСТОТИ
ОБЕРТАННЯ ВАЛА

 

1. Мета роботи

Ознайомитися з конструкцією й технічною характеристикою лабораторної установки ДМ 36 для визначення критичної частоти обертання вала, особливостями користування нею; розрахунком і експериментально визначити критичну частоту обертання вала; дослідити вплив відстані між опорами й розміщення диска на валу на величину критичної частоти.

 

2. Теоретичні відомості

У коливаннях, що спостерігаються в машинах, бере участь зазвичай значна частина всієї системи, зокрема: основний кінематичний ланцюг, основні несучі деталі.

Самостійні коливання передавальних валів, типу валів редукторів, не відіграють суттєвої ролі в динаміці машин, і тому їх окремо не розглядають. Навпаки, коливання корінних валів, що разом із приєднаними до них вузлами й опорами обертаються з високою швидкістю, (роторів турбін, колінчастих валів поршневих двигунів, шпинделів верстатів із оброблюваними деталями й т. п.) можуть виявитися визначальними.

Коливання валів та осей зумовлюються різноманітними чинниками: періодичною зміною передаваної навантаги, незрівноваженістю обертових мас, нерівномірністю розподілу навантаг у зонах спряження валів з іншими деталями тощо. Періодична зміна жорсткості опор і зачеплень також є джерелом коливань.

Колову частоту змушених коливань вала (осі) позначатимемо _, колову частоту власних (вільних) коливань – . У разі, коли колова частота змушених коливань вала збігається із частотою його власних коливань, або коли ці частоти є кратними, відбувається різке зростання амплітуди коливань, що може призвести до руйнування вала. Описане явище носить назву резонансу. Про наближення резонансу свідчить поява сильної вібрації. Колову частоту змушених коливань вала, що відповідає резонансу, називають критичною коловою частотою й позначають .

Найхарактернішими для валів є поперечні, або згинальні, кутові, або крутильні, і згинально-крутильні коливання. Два останні види коливань мають значення переважно для привода загалом, тому розрахунки на ці коливання розглядаються в спецкурсах.

Розглянемо поперечні коливання валів. Більшість швидкохідних валів зазнають дії змінних за модулем або напрямком сил, перпендикулярних до осі обертання, наприклад сил, спричинених незбалансованістю мас, що виникає через неточності виготовлення та монтажу вала й установлених на ньому деталей. Під дією цих сил (їх називають збуджуючими силами) й виникають поперечні коливання вала. Колова частота дії збуджуючих сил, а отже й колова частота змушених поперечних коливань вала, зазвичай дорівнюють його кутовій швидкості , тобто .

Отже, розрахунок валів на поперечні коливання для запобігання резонансу в умовах усталеного режиму роботи полягає у відшуканні критичної кутової швидкості  та відповідної їй критичної циклічної частоти  обертання вала й у перевірці умови відсутності резонансу, відповідно до якої значення кутової швидкості вала не має збігатися зі значенням  або бути близьким до нього. Небезпека резонансу існує, коли кутова швидкість знаходиться в проміжку від  до ; отже, робочу кутову швидкість валів слід призначати:  – для жорстких валів;  – для гнучких валів.

Критичну частоту обертання вала знайдемо на підґрунті таких міркувань.

Нехай на валу діаметром , установленому на двох опорах (рис. 3.1, а), прогон між якими , на відстані  від лівої опори розміщується диск масою  зі зміщеним від геометричної осі вала на деяку величину , що називається ексцентриситетом, центром ваги (Ц. в.). Власну масу вала  уважатимемо малою проти маси диска й до уваги не братимемо. Отже, маємо невагомий вал із зосередженою масою , тобто пружну систему з одним ступенем вільності.

З початком обертання вала з незбалансованою масою , виникне початкова відцентрова сила інерції:

, Н,                                             (2.1)

від дії якої вал зазнáє поперечного згину й прогнеться. Прогин вала позначатимемо . Надалі вал обертатиметься зігнутим і перебуватиме під дією відцентрової сили інерції:

 , Н,                                      (2.2)

де  – радіус обертання зосередженої маси  (центра ваги диска), м.

Вочевидь, що початкова відцентрова сила інерції  є складовою відцентрової сили інерції .

У здеформованому валі виникає сила пружного опору вала поперечному деформуванню , яка прагне відновити початкову форму вала, тобто є відновлюючою силою. Формула для її визначення має вигляд:

 , Н,                                           (2.3)

де  – згинальна жорсткість вала (величина, чисельно рівна силі, що спричиняє одиничний прогин вала), Н/м.

У разі рівномірного обертання відцентрова сила інерції  зрівноважується силою пружного опору вала , тобто виконується умова: , – або: , звідки:

 , м.                                     (2.4)

Розглянемо рух зосередженої маси . Рівняння руху дістанемо, скориставшись принципом Д’Аламбера. Оскільки маса  здійснює криволінійний (коловий) рух у площині, перпендикулярній до осі обертання, розглядатимемо його в системі координат  (рис. 2.1), початок якої сумістимо з віссю обертання.

 

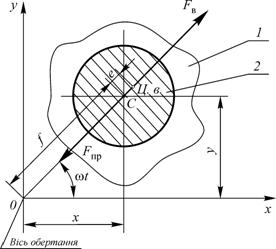
Рис. 2.1. Розрахункова схема вала

з незрівноваженим диском

Складаючи рівняння рівноваги, до проекцій сили  (, Н; , Н, де  та  – проекції прогину  вала, м), яка є зовнішньою щодо зосередженої маси , додамо відповідні проекції відцентрової сили інерції , що виникає під час руху маси :

   

або, після виконання диференціювання:

                                   (2.5)

де: ; ;  – час.

У результаті дістаємо диференціальні рівняння руху зосередженої маси :

                                    (2.6)

Рівняння (2.6) описують обертовий рух пружно зігнутого вала, який формально можна розглядати як змушені гармонійні поперечні коливання вала з амплітудою  відносно осі обертання як положення рівноваги*. Збуджуючими силами є проекції початкової відцентрової сили інерції: , Н, та , Н, які, унаслідок обертання вектора сили  зі сталою коловою частотою , змінюються в часі за гармонійним законом. Амплітуда збуджуючих сил .

Колова частота власних коливань вала , що фігурує в рівняннях (2.6), визначається за формулою:

 , с^–1.                                         (2.7)

Формулу (2.4), з урахуванням виразу (2.7), можна подати в такому записі:

 , м.                                     (2.8)

Ураховуючи те, що, унаслідок неминучої наявності всіляких опорів** (внутрішнє тертя в матеріалі вала, який зазнає циклічного деформування, опір оточуючого середовища та спряжених із валом деталей тощо), власні коливання завжди загасають і досить швидко припиняються, розв’язки рівнянь (2.6) запишемо у вигляді, відповідно:

                              (2.9)

 

Амплітуда змушених коливань: ,  м, що повністю збігається з виразом (2.8) для прогину вала.

 

*Слід зазначити, що за своєю фізичною суттю обертання пружно зігнутого вала якісно відрізняється від власне поперечних коливань.

**Сили опору в рівняннях рівноваги, задля спрощення теоретичних досліджень, не враховано.

З аналізу формули (2.8) випливає, що з ростом кутової швидкості  вала від 0 до  його прогин (амплітуда коливань)  збільшується, а коли  – , тобто настає резонанс, і вал може зруйнуватися (зламатися).

Отже, ми довели умову виникнення резонансу, сформульовану вище.

Критична кутова швидкість:

 , с^–1.                                   (2.10)

Як видно з формули (2.8), наявність навіть щонайменшого ексцентриситету може призвести в умовах резонансу до руйнування вала; тому, виготовляючи швидкохідні вали, слід приділяти особливу увагу їхньому балансуванню й центруванню встановлених на них деталей.

Частота власних поперечних коливань вала, здійснюваних за одну секунду, визначається за формулою:

 , Гц.                                        (2.11)

Звідси:

 , с^–1.                                          (2.12)

Оскільки критична частота обертання вала , хв.^–1, то, з урахуванням формули (2.12) і того, що :

 , хв.^–1.                                        (2.13)

Виразивши масу  через силу ваги : ,
де  м/с² – прискорення вільного падіння, дістанемо, що

 , с^–1.                                      (2.14)

Згинальна жорсткість  вала може бути знайдена з виразу для прогину вала. Для вибраної розрахункової схеми вала прогин від дії сили : , – звідки:

 , Н/м,                                (2.15)

де  – модуль поздовжньої пружності матеріалу вала, Па; , м⁴ – осьовий момент інерції площі поперечного перерізу вала.

За означенням, згинальна жорсткість вала чисельно дорівнює силі, що спричиняє його прогин на величину, рівну одиниці довжини. Якщо вал навантажується силою ваги , то  (величина, обернена до жорсткості, називється піддатливістю й дорівнює прогину вала від одиничної сили: , м/Н), де  – статичний прогин вала від дії сили , м. Звідси:

 , м.                                           (2.16)

Підкореневий вираз у формулі (2.14) містить величину, обернену до статичного прогину . Отже, критичну кутову швидкість вала можна виразити через його статичний прогин:

    , с^–1,                                      (2.17)

або:

 , с^–1.                                       (2.18)

Критична частота обертання вала, з урахуванням формули (2.17):

    , хв.^–1,                                 (2.19)

або:

 , хв.^–1.                                   (2.20)

У загальному випадку статичний прогин вала визначається методами опору матеріалів. Для визначення статичного прогину валів, які відповідають основним розрахунковим схемам, можна скористатися готовими формулами, що є в літературі. Так, наприклад, для вибраної розрахункової схеми вала:

 , м.                                (2.21)

Критичну частоту можна визначити точніше, якщо врахувати власну масу вала , що є доцільним тоді, коли вона не є малою проти маси встановлених на валу деталей. Найпростіше це зробити, додавши до зосередженої маси (у нашому випадку вона дорівнює масі диска ) зведену масу вала. Коефіцієнт зведення власної маси вала , для двоопорного вала із зосередженою масою посередині, який зазнає поперечних коливань, становить: . Отже, розрахункова маса системи, з урахуванням власної маси вала, буде визначатися за формулою:

 , кг.                                      (2.22)

Вираз у правій частині формули (2.8) можна записати дещо інакше:

 , м.                                   (2.23)

Аналіз формули (2.23) показує, що в разі, коли  (докритична область кутових швидкостей),  та  мають однакові знаки, тобто додаються (фаза змушених коливань і фаза збуджуючої сили збігаються), що відповідає обертанню вала за схемою рис. 3.1, а. Коли  (закритична область кутових швидкостей), знаки  та  протилежні (зсув фази змушених коливань щодо фази збуджуючої сили на кут ). Отже, у закритичній області з ростом  прогин вала зменшується, а коли  – , тобто центр ваги наближається до осі обертання вала, і зігнутий вал обертається навколо центра ваги. Таке явище називають динамічним самоцентруванням вала в закритичній області кутових швидкостей.

Більшість валів працюють у докритичній області. Аби зменшити небезпеку резонансу, уживають заходів для забезпечення їхніх антирезонансних властивостей: підвищують жорсткість валів, збільшуючи діаметр або зменшуючи відстань між опорами, підвищуючи тим самим частоту власних поперечних коливань.

У високошвидкохідних машинах (центрифуги, сепаратори, турбіни) застосовують вали, що працюють у закритичній області. Для уникнення руйнування під час переходу через зону резонансу, такі вали мають вільно прогинатися під дією відцентрової сили інерції, а отже мають бути гнучкими, з малою частотою власних коливань; тому їх виготовляють підвищеної піддатливості. Розганяючи або гальмуючи вал, перехід через критичну частоту обертання здійснюють якомога хутчій. Тривала робота вала в зоні резонансу неминуче призведе до його руйнування. Однак, завдяки наявності опорів коливальному руху, про які йшлося вище, руйнування вала не може відбутися миттєво, і тому, якщо перехід у закритичну область був здійснений достатньо швидко, роботоздатність вала збережеться уповні. Проте, для запобігання небезпечному наростанню амплітуд коливань вала під час його проходження через резонансну зону, варто передбачити додаткові спеціальні пристрої – обмежувачі амплітуд коливань, – а встановлені на валу деталі слід старанно збалансувати.

Для відшукання критичної частоти складніших систем, у тому числі багатомасових, може бути застосований підхід, аналогічний до розглянутого, або інші методи теоретичної механіки та опору матеріалів. Для систем із більш ніж одним ступенем вільності становить інтерес зазвичай найменша критична частота (вона відповідає основній частоті власних коливань системи), яка є найнебезпечнішою.

 

3. Лабораторне устаткування

1.    Лабораторна установка ДМ 36 для визначення момента тертя у вальницях котіння.

2.    Індикатор годинникового типу.

Схему лабораторної установки ДМ 36 подано на рис. 3.1.

Вал регульованого електродвигуна 1 за допомогою пружної муфти 2 з’єднано з випробуваним валом 3 (далі – просто “вал”), який установлено на опорах 4 й 5. На вал насаджено диск 6 зі зміщеним від геометричної осі вала на величину  центром ваги. Відстань  між опорами вала можна змінювати за допомогою маховичка 7. Обертаючи його, ми зміщуватимемо мутру (гайку)-корпус 8 разом із установленою в ній кульковою вальницею 5 уздовж осі ґвинта 9 і корпуса 10 правої опори вала. Можливість пересування вальниці 5 на валу забезпечується наявністю спеціальноого затискача, що з’єднує вал із внутрішнім кільцем вальниці.

На установці ДМ 36 маємо змогу визначити дослідним способом статичний прогин і критичну частоту обертання вала.

Для визначення статичного прогину вала на диск навішують скобу 11 із вантажем 12 (рис. 3.1, б). Це здійснюється за допомогою важеля, розміщеного на корпусі установки. Скоба має увійти в колову западину, що є на диску. Захисний кожух із закріпленим на ньому індикатором годинникового типу 13 розмістити так, щоб підпружинений вимірювальний стрижень індикатора доторкався до диска. Вивільнивши диск від навішеної на нього скоби зняти показник індикатора й обчислити за цим показником значення статичного прогину вала.

 

 

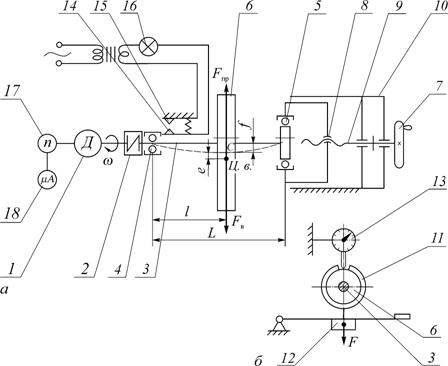
Рис. 3.1. Схема лабораторної установки ДМ 36

для визначення критичної частоти обертання вала:

а – загальна схема установки;

б – схема визначення статичного прогину вала

 

Критична частота обертання вала визначається так. Пустити електродвигун, здійснити його розгін і вихід на усталений режим обертання вала. Вал під дією відцентрової сили інерції прогнеться (рис. 3.1, а). Подальше нарощування частоти обертання призведе до збільшення прогину вала. У момент резонансу прогин досягне максимуму, вал натисне на рухомий підпружинений контакт 14 і замкне його з нерухомим контактом 15 – на панелі установки засвітиться зелена лампочка 16. Сигнал від тахометра 17, з’єднаного з валом електродвигуна, неперервно передається на встановлений на панелі установки міліамперметр 18, шкалу якого проградуйовано в об./хв., що дозволяє зафіксувати критичну частоту обертання вала в момент засвічування лампочки.

Змінюючи масу диска, розміщення диска на валу й відстань між опорами вала, можна дослідити залежність величини критичної частоти від цих параметрів. Конструкція установки дозволяє: змінювати  у межах 500…550 мм; розміщувати диск на валу на відстані до 25 мм ліворуч і праворуч від серединнного щодо опор вала положення; за рахунок приєднання до диска додаткових кілець збільшити його масу; створювати дисбаланс різної величини, заґвинтивши в диск ґвинт, який можна обтяжити іншими деталями (мутра, шайби).

 

Технічна характеристика лабораторної установки ДМ 36:

–  тип приводного електродвигуна – універсальний колекторний УЛ-062 (потуга – 180 Вт, максимальна частота обертання вала – 5000 хв.^–1, напруга – 220 В, частота струму – 50 Гц);

–  спосіб регулювання частоти обертання вала електродвигуна – безступінчастий за допомогою автотрансформатора РНО-250-0,5;

–  вимірювання статичного прогину вала – за допомогою індикатора годинникового типу із ціною поділки 0,01 мм;

–  вимірювання частоти обертання вала – за допомогою тахометра моделі ТГП-1 зі зніманням показників із міліамперметра моделі М-24;

–  діаметр вала – 12 мм;

–  маса вала – 0,5 кг;

–  маса диска – 2 кг;

–  відстань між опорами вала – 500 мм; 550 мм;

–  хід диска відносно серединного положення на валу – 25 мм;

–  зусилля статичного навантажування вала – 100 Н;

–  ексцентриситет – 0,245 мм;

–  габарити установки: довжина´ширина´висота – 1225´345´425 мм;

–  маса установки – 118 кг.

 

4. Порядок виконання роботи

4.1. Ознайомитися з теоретичними відомостями до роботи, конструкцією й технічною характеристикою лабораторної установки ДМ 36 та особливостями користування нею; викреслити схему установки (рис. 3.1) показавши всі основні вузли, пристрої, прилади та деталі й дати короткий опис установки.

4.2. У першому досліді: прáва опора вала розміщується в положенні, найвіддаленішому від лівої ( мм); диск установлено на валу на відстані  мм від лівої опори, тобто посередині між опорами; маса диска  кг; дисбаланс мінімальний ( мм).

4.2.1. З використанням формули (2.21) визначити розрахунковий статичний прогин вала , узявши для розрахунку:  МПа;  мм. Оскільки маса вала є співрозмірною з масою диска (кг), розрахункову масу системи слід узяти у відповідності з виразом (2.22).

4.2.2. Визначити статичний прогин вала експериментальним способом; для цього: навісити на диск скобу з вантажем, закріпивши на захисному кожуху індикатор підвести останній до диска, виставити на шкалі індикатора показник 0 (“нуль”), підняти скобу й зняти показник індикатора, який дасть нам значення статичного прогину вала з навішеною на диск скобою . За формулою (2.16) обчислити експериментальне значення статичного прогину вала, визначивши для цього згинальну жорсткість вала: , Н/м, де  Н – зусилля статичного навантажування вала.

Зіставити між собою експериментальне й розрахункове значення статичного прогину вала.

4.2.3. За залежністю (2.20) визначити розрахункову критичну частоту обертання вала.

4.2.4. Відвести індикатор від диска, зняти з диска скобу з вантажем, зняти індикатор, закрити кожух і пустити електродвигун.

4.2.5. Визначити критичну частоту обертання вала експериментально; для цього: плавно нарощуючи швидкість, довести вал до стану резонансу й не зупиняючи його якнайхудчій іще наростити швидкість перейшовши в такий спосіб у закритичну область; потім вал із закритичної області через стан резонансу повернути в докритичну область. Так повторити декілька разів щоразу фіксуючи за допомогою тахометра з міліамперметром частоту обертання вала  в момент входження в резонанс із докритичної області й  в момент входження в резонанс із закритичної області.

Обчислити усереднену експериментальну критичну частоту:

    , хв.^–1,                              (4.1)

й зіставити його з розрахунковою критичною частотою , обчисленою в п. 4.2.3.

4.3. Для проведення другого досліду установити диск у найближче до лівої опори положення ( мм). Виконати всі вимірювання й розрахунки за порядком, визначеним пп. 4.2.1…4.2.5.

4.4. Третій дослід проводиться для відстані між опорами  мм; диск розміти в найвіддаленіше від лівої опори положення ( мм). Виконати всі вимірювання й розрахунки за порядком, визначеним пп. 4.2.1…4.2.5.

4.5. Проаналізувати результати дослідження, зробити висновки й оформити звіт про виконання лабораторної роботи.

 

5. Форма та зміст звіту

про виконання роботи

Звіт виконується в тонкому зошиті в клітинку або на аркушах білого паперу формату А4, які потім мають бути зшиті. Поля обов’язкові.

 

 

ЗВІТ

про виконання лабораторної роботи 4:

“Визначення критичної частоти обертання вала”

 

1. Мета роботи

2. Схема лабораторної установки та її короткий опис

3. Результати вимірювань і розрахунків

Указівка. Виконати й записати всі розрахунки за змістом пп. 4.2…4.4; результати вимірювань і розрахунків занести до таблиць 3.1 і 3.2.

Таблиця 3.1

Таблиця 3.2

 

4. Аналіз результатів дослідження й висновки

 

6. Контрольні запитання

  1. Мета проведення досліджень.

  2. Які чинники зумовлюють прогин вала під час його обертання?

  3. Що таке критична частота обертання вала?

  4. Поясніть суть явища резонансу.

  5. Які зовнішні прояви резонансу?

  6. В якій зоні, дорезонансній чи зарезонансній, є доцільнішою робота машин із швидкохідними гнучкими валами?

  7. Що таке динамічне самоцентрування вала?

  8. Як експериментальним способом визначити статичний прогин вала?

  9. Чи можна визначити частоту власних поперечних коливань вала, знаючи величину його статичного прогину?

10. Яка методика визначення критичної частоти обертання вала на установці ДМ 36?

11. Від яких параметрів і як залежить величина критичної частоти обертання вала?

 

Список літератури

 

1. Деталі машин. Методичні вказівки до виконання лабораторних робіт: Навчально-методичний посібник для студентів інженерно-технічних спеціальностей: У 3-ьох ч. Ч.2 / Уклад. В.Байбула, Д.Коновалюк, М.Ярошевич; За ред. В.Байбули. – Луцьк: Ред.-видавничий від. ЛДТУ, 2001. – 48 с.

2. Гузенков П.Г. Детали машин. – М.: Высш. школа, 1982. – 351 с.

3. Иванов М.Н. Детали машин. – М.:Высш. шк., 1991. – 383 с.

4. Кудрявцев В.Н. Детали машин. – Л.: Машиностроение. Ленингр. отд-ние, 1980. – 464 с.

5. Опір матеріалів / Г.С.Писаренко та ін. – К.: Вища шк., 1993. – 655 с.

6. Павлише В.Т. Основи конструювання та розрахунок деталей машин: Підручник. – 2-е вид. перероб. – Львів: Афіша, 2003. – 560 с.

7. Прикладная механика. Лабораторный практикум. Учебное пособие / В.Ф.Мальцев, И.Ф.Сорока, В.И.Крупский и др. – Киев, Одесса: Вища школа, 1988.

8. Решетов Д.Н. Детали машин. – М.: Машиностроение, 1989. – 496 с.

9. Тарг С.М. Краткий курс теоретической механики. – М.: Наука, 1968. – 480 с.

10. Коновалюк Д.М., Ковальчук Р.М. Деталі машин: Підручник: Друге видання. – К.: Кондор, 2004. – 584 с.

11. Коновалюк Д.М., Ковальчук Р.М., Байбула В.О., Толстушко М.М. Деталі машин. Практикум. Навчальний посібник. – К.: Кондор, 2009. – 278 с.