7.7. Розрахунок валів для запобігання поперечним
коливанням
Більшість швидкохідних валів знаходяться під дією змінних за
модулем або напрямом сил, перпендикулярних до осі обертання, наприклад сил,
спричинених дисбалансом встановлених на них деталей. Частота таких збурюючих
сил переважно дорівнює частоті обертання вала. Якщо частота збурюючих сил
стає рівною частоті власних коливань вала, то настає явище резонансу, коли амплітуда коливань різко зростає і може
досягнути такого значення, при якому відбудеться руйнування вала. Кутова
швидкість вала, що відповідає резонансним коливанням, називається критичною кутовою швидкістю ωкр.
Розрізняють згинальні та крутильні коливання валів. Крутильні
коливання мають суттєве значення під час розрахунків валів із великими
приєднаними до них масами, наприклад роторів потужних турбін.
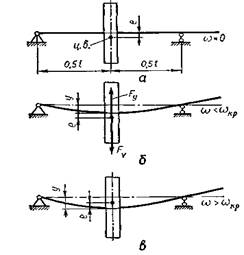
Рис. 11
Розрахунок валів для запобігання поперечним коливанням полягає у перевірці умови відсутності резонансу під час
усталеного режиму роботи. Відповідно до цієї умови фактична кутова швидкість
обертання не повинна знаходитись у межах від
0,7 · ωκρ до 1,3
· ωкр, тобто:
0,7 · ωκρ > ω >
1,3 · ωкр. (13)
Критичну кутову швидкість вала визначимо на основі
таких міркувань. Припустимо, що на валу симетрично щодо опор розміщений диск
масою m, центр ваги якого
зміщений відносно геометричної осі обертання на величину е (р.11 а).
Під час обертання вала під дією відцентрової сили Fv на диск відбувається
його поперечний згин. При кутовій швидкості ω прогин вала буде у (рис. 11, б), а відцентрова сила:
Fv = m · ω2
· (у + е).
(14)
Відцентрову силу Fv
зрівноважує сила поперечної пружності вала:
Fnp = k · y, (15)
де k – згинальна жорсткість вала (сила,
що спричинює прогин вала на
З усталеним режимом обертання вала зберігається умова Fv = Fnp,
тобто:
m · ω2 · (y
+ e) = k · y,
звідки можемо дістати
вираз для прогину вала:
у = m · ω2
· e / (k – m · ω2). (16)
З аналізу виразу (16) випливає, що при k = m · ω2 прогин у = ∞, тобто наступає резонанс.
Резонансна, або критична, кутова швидкість вала
![]() . (17)
. (17)
Формулу можна подати і в іншому вигляді. Якщо взяти m = G
/ g, де G – власна вага диска, g – прискорення вільного падіння, a G / k = yст – статичний
прогин вала під дією власної ваги диска, то
![]() . (18)
. (18)
Для схеми на рис. 11, б згинальна
жорсткість вала може бути визначена, якщо записати прогин вала у вигляді:
у = Fv
· l3 / (48 · E · I) = k
· y · l3 / (48 · E · I).
Звідси маємо:
k = 48 · E · I / l3. (19)
Отже, маючи критичну кутову швидкість ωκρ
вала заданих розмірів, за умовою (13) можна перевірити відсутність резонансу
при усталеному режимі обертання з кутовою швидкістю ω.
Aналіз формули (16) показує, що при ω < ωκρ
(дорезонансний режим обертання вала) знаки е та у однакові, що відповідає
обертанню вала за схемою рис. 11, б. Якщо
ω > ωκρ (зарезонансний режим обертання вала),
знаки при е та у протилежні.
В цьому випадку при ω → ∞ y → – е, тобто центр ваги (ц. в.) диска
наближається до геометричної осі обертання вала (рис. 11, в). Таке явище називають самоцентруванням вала в закритичній
області кутових швидкостей.
Більшість валів працює в докритичній області. Щоб зменшити небезпеку
резонансу, треба підвищити згинальну жорсткість валів і тим самим збільшити
критичну кутову швидкість. При високих швидкостях обертання, наприклад у
швидкохідних центрифугах та турбінах, застосовують вали, що працюють у
закритичній області. В таких випадках слід передбачати додаткові спеціальні
пристрої, що зменшують прогини валів під час переходу через резонансну
область.

