2.12. КОНІЧНІ ЗУБЧАСТІ ПЕРЕДАЧІ

 

Особливості конічних зубчастих передач.  Конічні зубчасті передачі застосовуються в тих випадках, коли осі валів перетинаються. Кут між осями валів може бути довільним, але на практиці найширше розповсюджені конічні зубчасті передачі з міжосьовим кутом Σ = 90°. Такі передачі називають ортогональ­ними.

Конічна зубчаста передача (рис. 28) складаєть­ся з двох зубчастих коліс, початковими поверхнями яких є бічні поверхні прямих кругових конусів, вписаних у сферу радіуса R_e так, що їхні вершини знаходяться у центрі сфери. Зубці на бічних поверхнях конусів відрізняються від зубців циліндричних коліс тим, що їхні розміри в поперечному пе­рерізі поступово зменшуються з на­ближенням до вершин конусів.

Під час обертання зубчастих коліс початкові конуси з кутами при вершинах δ₁ і δ₂ перекочують­ся один по другому без ковзання.

Профілі зубців конічних зубча­стих коліс так само, як і циліндрич­них, окреслюються евольвентою. Евольвента повинна утворюватись на сфері радіусом R_e, оскільки до­вільні точки контакту спряжених профілів зубців повинні  знаходи­тись на однаковій відстані від точ­ки О. Цій умові задовольняють точ­ки, що лежать на поверхні сфери. Профілювання  зубців на сфері утруднене, бо поверхня сфери не розгортається  на площину. Прак­тично  профілювання зубців здій­снюється наближено на поверхнях додаткових конусів із  твірними О₁А та 0₂A, перпендикулярними до спільної твірної ОА початкових конусів.

Зазначені особливості роблять конічні передачі складнішими, ніж циліндричні у виготовленні та монтажі. Для нарізування зубців ко­нічних коліс потрібне спеціальне обладнання та інструменти. Крім допусків на розміри зубчастих вінців, тут треба забезпечити допуски на кути Σ, δ₁ і δ₂, а при монтажі – збіг вершин конусів з точкою перетину осей валів. Виготовити конічну зубчасту передачу з одним і тим же ступенем точності значно важче, ніж циліндричну.

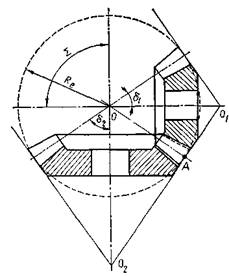
Рис. 28. Утворення конічної зубчастої передачі

 

Оскільки осі валів перетинаються, то виникають труднощі з роз­міщенням опор валів конічної передачі. В більшості випадків одне з конічних коліс розміщують консольнo на валу. При цьому збільшу­ється нерівномірність розподілу навантаження по довжині зубців. За дослідними даними несуча здатність конічної зубчастої передачі суттєво нижча від циліндричної з порівняльними розмірами і стано­вить близько 85 %. ККД конічної зубчастої передачі становить 0,95 – 0,96. Конічні зубчасті колеса бувають із прямими, тангенціальними та круговими зубцями.

Розміри зубців та вінців конічних зубчастих коліс. Конічна зуб­часта передача з основними розмірами вінців зубчастих коліс пока­зана на рис. 39.

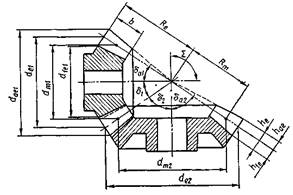
Рис. 29. Параметри конічної зубчастої передачі

В ортогональній конічній передачі міжосьовий кут Σ = δ₁ + δ₂= 90°, де δ₁ – кут при вершині ділильного конуса шестірні, а δ₂ – кут при вершині ділильного конуса колеса (у некоригованій передачі початковий та ділильний конуси збігаються).

Якщо число зубців конічної шестірні z₁ а колеса z₂, то кути при вершинах ділильних конусів визначають за формулами:

tg δ₁ = z₁/z₂;    tg δ₂  = z₂/z₁ = 90° – δ₁. (75)

Число зубців умовного плоского колеса діаметра d = 2R_e (рис. 29)

                          (76)

Модуль зубців конічних зубчастих коліс не е постійним у різних нормальних перерізах зубців. Тому вибір стандартного модуля тут втрачає зміст. Однак часто з метою полегшення контролю конічних зубчастих коліс за стандартний беруть модуль у зовнішньому нормаль­ному перерізі зубців. Такий модуль називається зовнішнім коловим модулем і позначається m_e. Надалі будемо брати до уваги, що зов­нішній коловий модуль зубців стандартний.

Початковий контур конічних зубчастих коліс стандартизований. Згідно з ГОСТ 13754–81 для m_e ≥ 1 мм регламентують такі пара­метри початкового контура: кут профілю зубця α = 20°; коефіцієнти – висоти головки зубця h^*_a = 1, радіального зазору с^* = 0,2, висоти ніжки зубця h^*_f = h^*_a + c^* = 1,2, радіуса кривини перехідної кривої у граничній точці профілю ρ^*_f ≥ 0,2, але не більш ніж 0,3.

Згідно з параметрами стандартного початкового контура розміри зубців конічних зубчастих коліс (рис. 29) визначаються за форму­лами:

– зовнішня висота головки зубця: h_ae = h^*_a · m_e = m_e;

– зовнішня висота ніжки зубця: h_fe = h^*_f · m_e = 1,2 · m_e;

– зовнішня висота зубця: h_e = h_ae + h_fe = 2,2 · m_e;

– радіальний зазор: с = с^* · m_e = 0,2 · m_e.

Розміри вінців конічних шестірні та колеса:

– зовнішні ділильні діаметри: d_e1 = m_e · z₁,    d_e2 = m_e · z₂;

– зовнішні діаметри вершин зубців:

d_ae1 = d_e1 + 2h_ae · cos δ₁ = d_e1 + 2m_e · cos δ₁,

d_ae2 = d_e2 + 2h_ae · cos δ₂ = d_e2 + 2m_e · cos δ₂,

– зовнішні діаметри впадин:

d_fe1 = d_e1 – 2h_fe · cos δ₁ = d_e1– 2,4m_e · cos δ₁;

d_fe2 = d_e2 – 2h_fe · cos δ₂ = d_e2– 2,4m_e · cos δ₂;

– зовнішня конусна відстань: R_e = 0,5 · m_e · z_с;

– коефіцієнт ширини зубчастого вінця: К_ье = b/R_e = 0,..0,30;

– ширина зубчастого вінця: b = К_ье · R_e ,    але за умови, що b ≤ 10m_e;

– середня конусна відстань: R_m = R_e – 0,5b;

– середній коловий модуль зубців: m_m = m_e · R_m / R_e;

– середні ділильні діаметри шестірні та колеса: d_m1 = m_m · z₁; d_m2 = m_m · z₂;

– кути головки   θ_а та ніжки   θ_f,  зубця:     tg θ_а = h_ae / R_e;      tg θ_f= h_fe / R_e ;

– кути конуса вершин зубців шестірні та колеса:

δ_a1 = δ₁+ θ_а;    δ_a2 = δ₂+ θ_а;

– кути конуса впадин шестірні та колеса:

δ_f1 = δ₁+ θ_f;    δ_f2 = δ₂+ θ_f.

Додаткові співвідношення між розмірами елементів конічної зуб­частої передачі, які будуть використані у подальших теоретичних викладках: передаточне число конічної зубчастої передачі:

u = ω₁/ ω₂ = d_e2/d _e1 = d_m2/d_ml = z₂/z₁,

– кути при вершинах початкових конусів шестірні та колеса:

tg δ₁ = l / u;    tg δ₂ = u;

– зовнішня конусна відстань: R_e= =  ;

– ділильні діаметри, виражені через R та  u,

d_e1 = 2 R_e /;        d_e2 = 2 R_eu /;

d_m1 = 2R_m /;               d_m2=2R_mu /;

– середня конусна відстань, середній коловий модуль та середні ділильні діаметри:

R_m = R_e– 0,5b = R_e · (1– 0,5K_be);

m_m = m_е· ( 1 – 0,5К_Ье);

d_m1 = d_el · (1– 0,5/K_bе);

d_m2 = d_e2 · (1– 0,5/K_be).

Заміна конічної зубчастої передачі еквівалентною прямозубою циліндричною передачею. Щоб спростити виклад при виводах розрахункових залежностей для оцінки міцності зубців конічних передач, замінимо конічну зубчасту передачу еквівалентною прямозубою циліндрич­ною передачею (рис. 30). При цьому початкові циліндри еквівалентних коліс будуть розгортками додаткових конусів у середньому перерізі зубців.

Параметри еквівалентних циліндричних коліс:

– модуль зубців еквівалентних коліс m_c дорівнює середньому коловому модулю конічних коліс m_m;

– ширина вінця еквівалентних коліс b_v дорівнює ширині вінця конічних коліс   b;

– ділильні діаметри еквівалентних коліс:

d_v1 = 2R_m · tg δ₁ = d_ml ·;

d_v2 = 2R_m · tg δ₂ = d_m2 ·;

– число зубців еквівалентних коліс:

d_v1= m_v · z_v1 = m_m · z_l ·, звідки z_v1 = z₁ ·  = z₁ / cos δ₁;

d_v2= m_v · z_v2 = m_m · z₂ ·, звідки   z_v2 = z₂ ·  = z₂ / cos δ₂.

– передаточне число еквівалентної передачі:     u_v = z_v2 / z_v1 = u²;

– міжосьова відстань еквівалентної циліндричної передачі визначається як півсума діаметрів коліс d_v1 та d_v2:    а_w = d_v1 + d_v2 / 2.

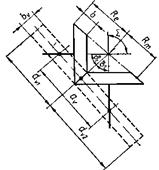
Рис. 30. До заміни конічних зубчастих коліс еквівалентними циліндричними

 

Номінальні сили у зачепленні прямозубих конічних коліс. За ана­логією з циліндричними передачами силу взаємодії зубців, розподілену по довжині їхнього контакту, замінимо зосередженою силою, яка прикладається до зубця у його середньому перерізі. Сили тертя між зубцями тут також не враховуєм.

У конічній передачі (рис. 31, а) взаємодія зубців показана у їх середньому нормальному перерізі А–А. Якщо до ведучого вала прикладений обертовий момент T₁, то з боку зубця шестірні на зу­бець колеса діє нормальна сила F_n, яка направлена вздовж нормалі до профілів зубців у точці їхнього контакту, тобто вздовж лінії за­чеплення, яка утворює кут зачеплення α з перпендикуляром до лінії центрів еквівалентних коліс. Силу F_n замінимо двома взаємно перпен­дикулярними складовими F_t та F₀, які перенесемо на схему переда­чі. Тут сила F_t проекціюється у точку Р, а сила F₀ направлена вздовж сліду площини А–А. Замінивши повторно силу F₀ двома взаємно перпендикулярними складовими F_r2 та F_a2, дістанемо в результаті три взаємно перпендикулярні компоненти нормальної сили F_n вза­ємодії зубців: F_t – колову силу; F_r2 – радіальну силу на колесі та F_a2 – осьову силу на колесі.

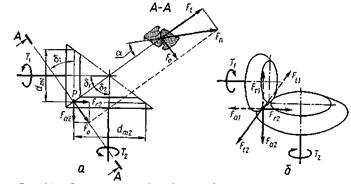
Рис. 31. Зусилля на зубці конічних зубчастих коліс

Колова сила направлена по спільній дотичній до конічних коліс і лежить у площині їхнього обертання. Тому ця сила може бути ви­значена через обертовий момент Т₁ за формулою:

F_l=2T₁/d_m1.                               (77)

Нормальна сила F_n і сила F₀ виражаються через колову силу F_t за залежностями (див. паралелограм сил у перерізі А–А на рис. 31, а):

F_n = F_t/cos α = 2T₁ /(d_m1 · cos α);        F₀ = F_t · tg α.  (78)

Подаючи сили F_r2 та F_a2 через F₀ (див. паралелограм сил на схемі передачі), дістаємо:

F_r2 = F₀ · cos δ₂ = F_t · tg α · cos δ₂;                        (79)

F_a2 = F₀ · cos δ₁ = F_t · tg α · cos δ₁.                        (80)

Отже, формула (78) дозволяє визначити нормальну силу F_n взаємодії зубців через обертовий момент T₁, а формули (74), (79) та (80) – її три складові, що діють на зубці конічного колеса; колову силу F_t, радіальну F_r2 та осьову F_a2.

Аналогічні складові діють з боку зубців конічного колеса на зубці шестірні, але у протилежному напрямі, до того ж радіальна сила на шестірні F_r1 дорівнює осьовий силі F_a2 на коле­сі, а осьова сила F_a1 на шестірні – радіальній силі F_r2 на колесі. Остаточно запишемо компоненти сили F_n взаємодії зубців конічної прямозубої передачі:

F_t = F_t1 = F_t2 = 2T₁/d_ml;

F_rl = F_a2 = F_t · tg α · cos δ₁;                              (81)

F_a1 = F_r2 = F_t · tg α · cos δ₂.

Зображення сили взаємодії зубців F_n конічних зубчастих коліс у формі трьох взаємно перпендикулярних складових (81) дає пев­ну зручність при складанні розрахункових схем валів передачі.

Розрахункове навантаження на зубці конічної зубчастої передачі. За аналогією з циліндричними зубчастими передачами розрахункове навантаження на зубці конічної передачі визначають за формулами: при розрахунку зубців на кон­тактну втому:

q_н = W_{H t} /(K_ε· ε_α· cos α);                   (82)

при розрахунку зубців на втому при згині     q_F = W_{F t} /( K_ε · ε_α · cos α).        

Під час визначення питомої розрахункової колової сили W_{H t} і W_{F t} треба враховувати такі особливості конічної зубчастої передачі. Несуча здатність конічної передачі становить приблизно 85 % від несучої здатності еквівалентної циліндричної передачі, тобто у конічній передачі тільки 85 % ширини вінця b ефек­тивно бере участь у передаванні навантаження. Тому для конічної зубчастої передачі питому розрахункову колову силу рекомендують визначати за формулами:

W_{H t} = [F_Ht /(0,85b)] · К_Hα· К_Hβ· К_HV,                       (83)

W_{F t} = [F_Ft /(0,85b)] · К_Fα· К_Fβ· К_FV.                       (84)

Тут колові сили F_Ht = F_Ft = F_t визначаються за виразом (77), а коефіцієнти К_α, К_β і К_V мають такий же зміст, як і в циліндрич­них передачах. Для прямозубих конічних передач К_Hα = К_Fα = 1. а коефіцієнти К_Hβ та К_Fβ знаходять за кривими 1–3 на рис. 32 залежно від схем 1–3 розміщення конічних коліс, виду опор валів, твердості активних поверхонь зубців та коефіцієнта K_bd:

К_bd = b/d_vl = [K_beR_e/(2R_m)] u = К_bеu / (2 – К_bе).             (31)

Коефіцієнти динамічного навантаження зубців К_HV та K_fv можна брати такі самі, як і для циліндричних зубчастих передач при коловій швидкості зубців v =0,5· ω₁· d_m1.

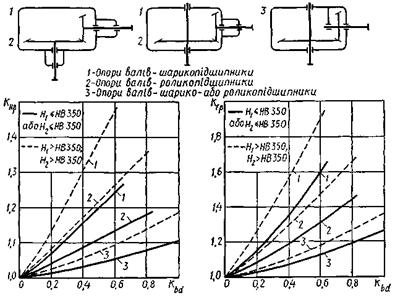
Рис. 32. Графіки для визначення коефіцієнтів К_Hβ та К_Fβ

 

Розрахунок активних поверхонь зубців на контактні втому та міцність. Розрахункову формулу для перевірки на контактну втому активних поверхонь зубців конічної зубчастої передачі можна дістати на основі залежності, яка використовується у розрахунках циліндричних зубчастих передач. Дістанемо розрахункову залежність для перевірки на контактну втому активних поверхонь зубців конічної зубчастої передачі у вигляді:

 .             (85)

Тут W_{H t} – питома розрахункова колова сила, яка визначається за виразом:

W_{H t} = [F_Ht /(0,85b)] К_HαК_HβК_HV.

Розрахункові коефіцієнти Z_M та Z_H в умові (85) беруть такими ж, як і для циліндричних передач, а коефіцієнт Z_ε = , де коефіцієнт торцевого перекриття ε_α можна знайти за числами зуб­ців Z_v1 та Z_v2 еквівалентних циліндричних коліс:

ε_α = 1,88 – 3,2 ( l / z_v1 + l / z_v2).                       (86)

Розрахунок на контактну міцність активних поверхонь зубців конічних зубчастих передач виконують як і у циліндричних передачах. Допусти­мі контактне напруження [σ]_н та граничне контактне напруження [σ]_{н max}  визначають згідно з рекомендаціями 11.( циліндричних передачах).

Розрахунок зубців на втому при згині та на міцність при згині максимальним навантаженням. Для розрахунку зубців конічних передач на втому при згині справедлива формула, яку дістали для циліндричних передач, тільки замість нормального модуля m_n, треба брати середній коловий модуль зубців m_m конічних коліс, що дорівнює модулю зубців m_v еквівалентної циліндричної передачі:

σ_f = Y_FY_ε Y_β W_{F t} / m_m ≤ [σ]_F.                                 (87)

Тут питома розрахункова колова сила визначається за формулою:

W_{F t} = [F_Ft /(0,85b)] К_FαК_FβК_FV.

Коефіцієнт форми зубців Y_F знаходять за даними табл. 5 залежно від еквівалентних чисел зубців Z_v1 та Z_v2. Для конічних передач із прямими зубцями коефіцієнти Y_ε = 1 та Y_β = 1.

Розрахунок зубців конічних передач на міцність при згині максимальним навантаженням виконують за аналогією з циліндричними передачами.

Міцність зубців на втому та на міцність при згині перевіряють окремо для зубців шестірні та зубців колеса. Якщо результати перевірки незадовільні, то треба збільшити модуль зубців m_m.

У проектному розрахунку конічної зубчастої передачі основний розмірний параметр визначають також із умови стійкості активних поверхонь зубців проти втомного викришування. Основним розмірним параметром ко­нічної передачі, що визначає її габаритні розміри, беруть зовнішній ділильний діаметр колеса d_e2.

Вихідними даними для проектного розрахунку передачі є такі:

– розрахункове тривало діюче навантаження   Т_1н:

– передаточне число передачі u;

– параметр    K_be = b/R_e або   К_ьd = b/d_v1 = К_ьеu / (2 – К_ье),

– вид передачі – із прямими, тангенціальними чи круговими зубцями;

– матеріали зубчастих коліс, термообробка їх та твердість активних поверхонь зубців, за цими даними попередньо визначають допустиме контактне напруження [σ]_H.

Розрахункову формулу для проектного розрахунку конічної зубчастої передачі дістанемо шляхом таких перетворень:

W_Ht / d_m1 = [F_t/(0,85bd_ml)] К_HαК_HβК_HV = [2  10³ T_1H /(0,85bd_ml)] К_HαК_HβК_HV.

Виразимо b і d_m1 через зовнішній ділильний діаметр колеса d_e2:

b = К_ьеR_е = K_be 0,5 d_el   =  0,5K_be d_e2 /;

d_m1 = d_e1 (1 – 0,5 K_be) = d_e2 (1 – 0,5 K_be) / u.

Підставивши відношення W_Ht / d_m1, в якому Ь та d_m1 подані через d_e2, у розрахункову залежність (74), можна знайти формулу для визначення мінімального зовнішнього ділильного діаметра конічного колеса:

d_{e2 min} = K_d .               (88)

Тут допоміжний коефіцієнт K_d об’єднує ряд коефіцієнтів і виражається залежністю

К_d = .

У проектному розрахунку прямозубої конічної зубчастої пере­дачі рекомендують брати: К_d = 1000 МПа¹/³ для сталевих коліс; K_d – 825 МПа¹/³ для чавунних коліс. Коефіцієнт К_Hβ визначають за графіками на рис. 5.

Слід зауважити, що T₁ беруть у ньютон-метрах (Н·м), [σ]_н – у мегапаскалях (МПа), a d_{e2 min} – у міліметрах (мм).

Щоб визначити модуль зубців, треба попередньо вибрати числа зубців шестірні та колеса. Число зубців конічної шестірні для сило­вих конічних передач рекомендується брати в таких межах:

z₁ = 17...20 при u = 1,0... 1,5;       z₁ = 13...18 при u = 2...4.

За вибраним числом зубців шестірні визначають число зубців конічного колеса z₂ = uz₁. При цьому бажано виконувати умову
 z₁ + z₂ ≤ 80 ..85.

Вибравши число зубців конічного колеса, можна визначити потрібний зовнішній коловий модуль:

 m’_e = d_{e2 min} /z₂,                                               (89)

який треба узгодити зі стандартним значенням   m_е.

Знаючи модуль m_е та число зубців коліс z₁ та z₂, можна знайти всі розміри вінців конічних зубчастих коліс.

У конічних зубчастих передачах перевага надається також маломодульним колесам (для силових передач m_е ≥ 1,5 мм), що досягається відповідним вибором чисел зубців шестірні та колеса.

 

 Особливості конічних зубчастих передач із непрямими зубцями

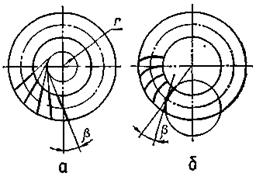
Рис. 33. Конічні колеса з непрямими зубцями

 

Прямозубі конічні передачі використовують з порівняно невисокими коловими швидкостями до 3 м/с (інколи до 8 м/с) за умови шліфування зубців та 6-го або 7-го ступенів точності. При більш високих швидкостях доцільно застосовувати конічні колеса із тангенціальними або круговими зубцями (рис. 33), які забезпечують більш плавне зачеплення, більшу несучу здатність і, крім цього, вони більш технологічні.

У конічних колесах із тангенціальними зубцями (рис. 33, а) лінія зубців напрямлена по дотичній до деякого додаткового кола радіуса r і утворює з твірною конуса кут β. Кут нахилу зубців β не повинен перевищувати 25–30°. Колова швидкість таких коліс може бути доведена до 15 м/с. Найбільш ефективні у силових передачах колеса з тангенціальними зубцями при m ≥ 8 мм.

У конічних колесах із круговими зубцями (рис. 33, б) лінія зубців має форму дуги кола, де рухається інструмент при нарізуванні зубців. Кут нахилу β кругового зубця змінний для різних перерізів зубця. За розрахунковий беруть кут нахилу зубців на колі середнього діаметра колеса. Для коліс із круговими зубцями β ≈ 35°. Використовують конічні зубчасті передачі з колесами з круговими зубцями у трансмісіях транспортних машин та у верстатобудуванні. Колова швидкість може досягати 30 м/с.

Для конічних коліс із тангенціальними зубцями за розрахунковий беруть зовнішній нормальний модуль m_ne, а для коліс із круговими зубцями – середній нормальний модуль m_mn.

Розрахунок конічних зубчас­тих передач з непрямими зубцями наведено у відповідній довідко­вій літературі, а їх розрахунки на міцність можна наближено виконувати, враховуючи деякі особливості цих передач при виборі розрахункових коефіцієнтів. Зараз широко застосовують спеціальні розрахунки конічних передач із круговими зубцями AGMA (США), що розроблені фірмою зуборізних верстатів «Глісон», яка має великий досвід у проектуванні, виг­товленні та випробуванні конічних зубчастих передач.