Тема 10. Взаємне розташування площин та прямих в просторі.

Приклад 1. Обчислити величину кута між прямими і

Розв'язання.

Напрямний вектор має координати . Знайдемо координати напрямного вектора другої прямої

.

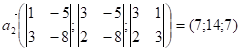Дія подальших обчислень зручно брати не вектор , а йому колінеарний . За формулою

,
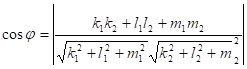де і - напрямні вектори відповідних прямих, одержимо , звідси .

Приклад 2. Встановити взаємне розміщення прямих та .

Розв'язання.

Координати напрямних векторів і даних прямих не пропорційні, значить прямі або перетинаються, або мимобіжні. Вони будуть перетинатися, якщо вектори , і , де , – будь-які точки, що належать відповідно першій і другій даним прямим, компланарні і будуть мимобіжними, якщо ці вектори не компланарні. В якості точок і візьмемо відомі точки і .

Знайдемо вектор : і знайдемо мішаний добуток векторів , і

.

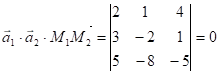Отже, дані вектори є компланарні, а тому відповідні прямі перетинаються.

Приклад 3. Скласти рівняння площини, що проходить через пряму перетину площин , і паралельної осі .

Розв'язання. Запишемо рівняння всіх площин, що проходять через задану пряму: або

.

Рівняння площини паралельної осі , має вигляд. Тоді якщо шукана площина належить пучку площин, то , звідси . Підставляючи в рівняння пучка площин і скоротивши на , одержимо шукане рівняння .

Приклад 4. З точки опустити перпендикуляр на площину

Розв'язання. В якості напрямного вектора а шуканого перпендикуляру можна взяти вектор даної площини. Тепер, знаючи точку і напрямний вектор прямої, запишемо її канонічне рівняння:

.

Приклад 5. Знайти точку перетину прямої і площини .

Розв'язання. __

Запишемо параметричне рівняння прямої

, , .

Підставимо значення в рівняння площини:

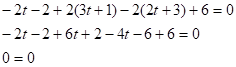
Отже, пряма лежить на площині .

Приклад 6. При якому значенні пряма паралельна площині .

Розв'язання. Пряма паралельна площині, якщо напрямний вектор прямої перпендикулярний нормальному вектору площини. Вектор – нормальний вектор площини, а вектор – напрямний вектор прямої, тому

.

Приклад 7. Знайти кут між прямою

(1) і площиною (2).

Розв'язання. Рівняння прямої (1) запишемо в канонічному вигляді. З першого рівняння системи (1) ; з другого рівняння , звідси:

або .

Отже , .

Для визначення кута використаємо формулу

.

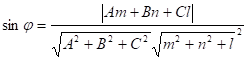В нашому випадку:

.

Приклад 8. Знайти відстань від точки до прямої
(1).

Розв'язання. Через дану точку проведемо площину , перпендикулярну до цієї прямої. Далі знайдемо точку перетину цієї площини з прямою (1). Відрізок буде лежати в площині , що перпендикулярна до прямої (1), отже він буде перпендикуляром, що опушений з точки на дану пряму, основою якого є точка найкоротша відстань від т. до даної прямої буде довжина перпендикуляра , проведеного з т. на пряму (1). Запишемо рівняння площини, що проходить через т. :

(2)

Визначимо коефіцієнти так щоб площина (2) була перпендикулякною до прямої (1). Використаємо умову перпендикулякності прямої площини

Покладемо ; ; одержимо

або

. (3)

Далі знайдемо точку перетину цієї площини з даною прямою

Звідси .

Відстань між точками і :

.