Лабораторна робота № 4

Тема. Перетворення двовимірних координат

Вступ

Перетворення координат широко використовується під час синтезу як статичних, так і динамічних зображень з метою реалізації таких операцій над рисунком, як перенесення, поворот, подібність, симетрія.

Перенесення є достатньо простою операцією, оскільки реалізується шляхом зміни значень першої і/чи другої координат. Інші операції, а тим більше їх комбінація, характеризуються більшою складністю і вимагають відповідних математичних перетворень.

У лабораторній роботі розглядаються тільки двовимірні перетворення. Звичайно в даному процесі початково задаються основні (первинні) координати х1, у1 а через них у вигляді рівнянь прораховуються вторинні координати х22, у22.

х22 = f(xl, yl),

у22 = f(xl, yl).

Найбільш поширені так звані афінні перетворення, які припускають збереження після розрахунку вторинних координат паралель і форми у прямих. Загальний вигляд рівнянь таких перетворень має вигляд:

x22 = axxxl+axyyl+ax,

у22 = аухх1 +аууу1+ау.

При цьому зсув без повороту характеризується матрицею коефіцієнтів:

,

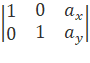де ах, ау - задають зсув відповідно по осях х і у, тобто х2 = xl+ах, у2=у1+ау.

Операція масштабування (перетворення подібності) реалізується матрицею:

.

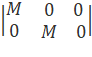Дзеркальне відображення щодо діагоналі першого квадранта (зміна координатних осей) припускає матрицю вигляду:

.

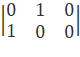Повороту на кут α проти годинникової стрілки відповідає матриця:

.

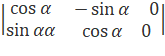Комбінації двох або більше операцій перетворення відповідає комбінація коефіцієнтів відповідних матриць. Так, наприклад, зсув із одночасним поворотом реалізується матрицею:

.

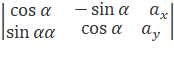Опис середовища програмування

Під час перетворення координат у середовищі мови програмування TurboPascal необхідно врахувати, що графічний екран ПК є четвертим квадрантом прямокутної системи координат, тобто початок координат знаходиться в лівому верхньому кутку. Повноцінна система координат створюється самим користувачем шляхом перенесення її початку вниз і/чи вправо на величини Δх і/чи Δу, тобто реалізується локальна система, зсунута на дані величини щодо глобальної. Надалі глобальні координати всіх точок (х_г, у_г) перераховуються через локальні (х_л, у_л) за такими рівняннями:

х_г = х_л+Δх,

у_г = Δу-у_л.

Друга проблема, що виникає звичайно при складних перетвореннях, − різна роздільна здатність (кількість пікселів на одиницю довжини) графічного екрану по горизонтали і вертикалі. Спроба зобразити квадрат шляхом задання однакової кількості пікселів по його сторонах приводить до відображення прямокутника, витягнутого по висоті. Даний ефект відсутній тільки за роздільної здатності 640×480 і особливо посилюється під час встановлення підрежимів з низькою кількістю пікселів по вертикалі, наприклад, 640×200. Для усунення вказаного ефекту засобами мови Паскаль проводиться попереднє масштабування зображення за допомогою процедури GetAspectRatio (mх, mу), де mх, mу − змінні, в які записується число точок по горизонталі і вертикалі. Надалі, під час побудови потрібного зображення всі координати по осі Х повинні множитися на відношення mу/mх, або, навпаки, всі координати по осі Y множаться на відношення mx/my. При цьому виникає ще одна проблема пов'язана з особливостями мови Паскаль, які отримуються під час множення. Масштабовані координати можуть приймати суттєві значення, що заборонено для параметрів графічних примітивів даної мови. Тому всі результати таких множень повинні округлятися функцією Round.

Приклад програми. У першому квадранті локальної системи координат зобразити прямокутник, ліва нижня точка якого має координати (10,10), а елементи зображення мають розмір не менше 50 пікселів і різне забарвлення, а потім перемістити його вгору на 120 і в право на 200 пікселів з поворотом за годинниковою стрілкою на 70°.

Лістинг програми

program dd;

uses crt,graph;

var dr,md,i:integer;

p:pointer; size:word;

begin

initgraph(dr,md,'');

setlinestyle(0,0,3);

setcolor(lightgreen);

rectangle(2,25,150,100);

size:=imagesize(0,0,153,103);

getmem(p,size);

getimage(0,0,153,103,p^);

cleardevice;

for i:= 1 to 100 do

begin

putimage(50,200-i,p^,0);

delay(5000);

end;

for i:= 1 to 150 do

begin

putimage(50+i,100,p^,0);

delay(5000);

end;

cleardevice;

line(215,150,255,100);

line(215,150,325,230);

line(325,230,360,175);

line(360,175,255,100);

readln;

end.

Варіанти завдань

Створити програму, що реалізує графічними засобами мови програмування TurboPascal зображення, включаючи: локальну систему координат; на початку першого квадранта координат початкове зображення, ліва нижня точка якого має координати (10, 10), а елементи зображення мають розмір не менше 50 пікселів і різне забарвлення; перетворене відповідно до завдання зображення.

1. —|— – подібна фігура дзеркально відображається щодо осі X і збільшується в 1,5 рази;

2. —|— – подібна фігура переміщається вгору на 90 і вліво на 150 пікселів із поворотом на 40° за годинниковою стрілкою;

3. ┌─ − подібна фігура дзеркально відображається щодо діагоналі першого квадранта і збільшується в 2 рази;

4. прямокутний трикутник переміщується вниз на 40 і вправо на 200 пікселів із поворотом проти годинникової стрілки на 50°;

5. дві вертикальні паралельні лінії і зсунути вгору і вправо на 100 пікселів і повернути на 30º проти годинникої стрілки щодо початку локальних координат;

6. Т − фігура дзеркально відображається на осі Y і повертається на 15° за годинниковою стрілкою;

7. |—| − подібна фігура зміщується на 120 і вліво на 140 пікселів з поворотом проти годинникової стрілки на 73°;

8. правильна трапеція відображається відносно діагоналі першого квадранта і зменшується в 2 рази;

9. ||- − подібна фігура повертається на 180° і збільшується в 1,3 рази;

10. зафарбований трикутник зміщується вліво на 230 і вниз на 50 пікселів з поворотом за годинниковою стрілкою на 49°;

11. -|—|- – подібна фігура дзеркально відображається відносно осі X з поворотом за годинниковою стрілкою на 36°;

12. зафарбований рівнобедренний трикутник зміщується вліво на 130 і вниз на 150 пікселів з поворотом за годинниковою стрілкою на 79°;

13. ± – подібна фігура зміщується вправо на 60 і вниз на 200 пікселів зі збільшенням в 2,3 рази;

14. ├ − подібна фігура дзеркально відображається відносно осі Y і зменшується в 1,4 рази;

15. X − подібна фігура повертається на 70° проти годинникової стрілки зі зміщенням вліво на 60 і вниз на 140 пікселів;

16. Δ – подібна фігура повертається на 180°, зміщуючись вліво і вниз на 100 пікселів;

17. Н – подібна фігура дзеркально відображається відносно діагоналі першого квадранта зі збільшенням в 1.5 рази;

18. И – подібна фігура дзеркально відображається відносно осі X з поворотом за годинниковою стрілкою на 34°;

19. N – подібна фігура зміщується вверх на 90 і вліво на 120 пікселів із поворотом за годинниковою стрілкою на 56°;

20. ┴┴ – подібна фігура зміщується вправо на 200 і вниз на 70 пікселів із збільшенням в 1,8 рази;

21. ┌┐ – подібна фігура зміщується вниз на 120 і вліво на 140 пікселів із поворотом проти годинникової стрілки на 73°;

22. │├ – подібна фігура повертається на 180° і збільшується в 1,3 рази;

23) ┼┼ – подібна фігура зміщується вправо на 200 і вниз на 70 пікселів із збільшенням у 1,8 рази;

24. ┌┘ – подібна фігура дзеркально відображається відносно осі X з поворотом проти годинникової стрілки на 54°;

25. Е – подібна фігура зміщується на 100 і вліво на 160 пікселів з поворотом проти годинникової стрілки на 23°;

26. П – подібна фігура зміщується вліво на 130 і вниз на 80 пікселів з поворотом за годинниковою стрілкою на 69°;

27. О – подібна фігура зміщується вверх на 90 і вліво на 120 пікселів із поворотом за годинниковою стрілкою на 26°;

28. L – подібна фігура зміщується вверх на 90 і вліво на 120 пікселів із поворотом за годинниковою стрілкою на 56°;

29. # – подібна фігура дзеркально відображається відносно осі У і зменшується в 1,4 рази;

30. ↑ – подібна фігура повертається на 180° і збільшується в 1,3 рази.

Зміст звіту

1) Зміст завдання;

2) лістинг програми;

3) надруковане зображення.

Контрольні питання

1. Які геометричні перетворення називаються афінними?

2. Які існують види геометричного перетворення?

3. Яким квадрантом прямокутної системи координат поданий екран дисплея по замовчуванню?

4. Для чого застосовується під час геометричної побудови процедура мови Паскаль GetAspectRatio?

5. Чи можна сумістити при геометричному перетворенні зсув і масштабування?