7.4. Загальний алгоритм Брезенхема

Для того, щоб реалізація алгоритму Брезенхема була повною, необхідно обробляти відрізки у всіх октантах. Модифікацію легко зробити, враховуючи в алгоритмі номер квадранта, в якому лежить відрізок і його кутовий коефіцієнт. Коли абсолютна величина кутового коефіцієнта більше 1, використовується для прийняття рішення про зміну величини . Вибір постійно змінюється (на +1 або −1) координати залежить від квадранта (рис. 7.7).

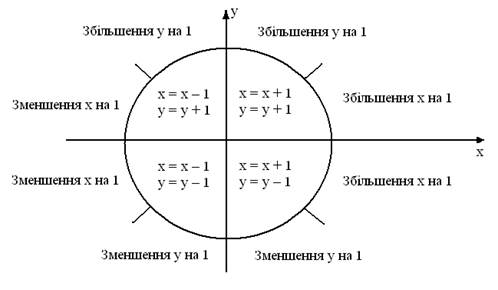
Рис. 7.7. Розбір випадків для узагальненого алгоритму Брезенхема

Загальний алгоритм може мати такий вигляд:

Ззагальнений цілочисельний алгоритм Брезенхема квадрантів

передбачається, що кінці відрізка і не збігаються

всі змінні вважаються цілими

функція Sign повертає -1, 0, 1 для негативного, нульового і позитивного аргументу відповідно

ініціалізація змінних

обмін значень та у залежності від кутового коефіцієнта нахилу відрізка

if then

тим =

Δy = тим

Обмін =1

else

Обмін = 0

end if

ініціалізація з поправкою на половину пікселя

основний цикл

for i = 1 to

Plot (x, y)

while ()

if Обмін = 1 then

else

end if

end while

if Обмін = 1 then

else

end if

next i

finish

Приклад 7.4. Узагальнений алгоритм Брезенхема

Для ілюстрації загального алгоритму Брезенхема розглянемо відрізок із точки (0, 0) в точку (-8, -4). У прикладі 7.2. цей відрізок був оброблений за допомогою простого ЦДА

початкові дані

Обмін = 0

послідовне виконання основного циклу

i	Plot	e	x	y
		0	0	0
1	(0, 0)
		−16	0	−1
		−8	−1	−1
2	(−1,−1)
		0	−2	−1
3	(−2, 1)
		−16	−2	−2
		−8	−3	−2
4	(−3,−2)
		0	−4	−2
5	(−4, 2)
		−16	−4	−3
		−8	−5	−3
6	(−5,−3)
		0	−6	−3
7	(−6, 3)
		−16	−6	−4
		−8	−7	−4
8	(−7, 4)
		0	−8	−4

На рис. 7.8 наведений результат. Результати роботи двох алгоритмів відрізняються, рис. 7.2 і 7.8.

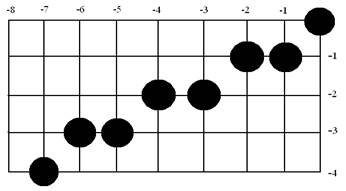
Рис. 7.8. Результат роботи узагальненого алгоритму Брезенхема в третьому квадранті