РОЗДІЛ 7. ПРАКТИЧНА ЧАСТИНА

7.1. Цифровий диференціальний аналізатор

Один з методів розкладання відрізка в растр полягає у вирішенні диференціального рівняння, що описує цей процес. Для прямої лінії маємо

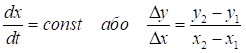
Рішення представляється у вигляді:

,

(7.1)

,

де , і , – кінці відрізка, який розкладається і – початкове значення для наступного кроку уздовж відрізка. Фактично рівняння (7.1) являє собою рекурентне співвідношення для послідовних значень уздовж потрібного відрізка. Цей метод, що використовується для розкладання в растр відрізків, називається цифровим диференціальних аналізатором (ЦДА). У простому ЦДА або , або (більше із збільшень) вибирається в якості одиниці растру. Нижче наводиться простий алгоритм, який працює у всіх квадрантах.

Процес розкладання в растр відрізка за методом цифрового диференціального аналізатора (ЦДА)

передбачається, що кінці відрізка і не збігаються.

Integer - функція перетворення дійсного числа в ціле.

Примітка: у багатьох реалізаціях функція Integer означає взяття цілої частини, тобто

Integer (-8.5) = -9, а не -8. У даному алгоритмі використовується саме така функція,

Sign - функція, що повертає -1, 0, 1 для негативного, нульового і позитивного аргументу відповідно апроксимуємо довжину відрізка

if then

Довжина =

else

Довжина =

end if

вважаємо більше із збільшень або рівним одиниці растра

Довжина

Довжина

округлюємо величини, а не відкидаємо дробову частину

використання знакової функції робить алгоритм придатним для всіх квадрантів

Sign

Sign

початок основного циклу

i = 1

while (i довжина)

Plot (Integer(x), Integer(y))

end while

finish

Наведемо приклад, що ілюструє роботу алгоритму.

Приклад 7.1. Простий ЦДА у першому квадранті.

Розглянемо відрізок з точки (0, 0) в точку (5, 5). Використовуємо ЦДА для розкладання цього відрізка в растр. Результати роботи алгоритму такі:

початкові дані

Довжина = 5

результати покрокового виконання основного циклу

i	Plot	x	y
1	(0, 0)	0.5	0.5
		1.5	1.5
2	(1, 1)
		2.5	2.5
3	(2, 2)
		3.5	3.5
4	(3, 3)
		4.5	4.5
5	(4, 4)
		5.5	5.5

Отримане растрове подання відрізка наведено на рис. 7.1. Зауважимо, що кінцеві точки визначені точно і вибрані пікселі рівномірно розподілені вздовж відрізка. Зовнішній вигляд прямої цілком задовільний. Однак, якщо початковим значенням змінної зробити нуль замість одиниці, то виявиться активованим піксель з координатами (5, 5), що не бажано. Якщо адреса пікселя задана цілими координатами лівого нижнього кута, то активація цього пікселя дасть явно невірну кінцеву точку відрізка (рис. 7.1). До того ж при виведенні серії послідовних відрізків піксель (5, 5) буде активований двічі, в кінці цього відрізка і на початку наступного. Такий піксель може виглядати як більш яскравий або мати інший (мабуть, неприродний) колір. Наступний приклад ілюструє роботу алгоритму в третьому квадранті.

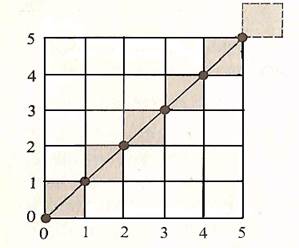
Рис. 7.1. Результати роботи простого ЦДА в першому квадранті

Приклад 7.2. Простий ЦДА в третьому квадранті.

Розглянемо відрізок з точки (0, 0) в точку (-8, -4) у третьому квадранті. Результати роботи алгоритму такі:

початкові дані

Довжина = 8

результати покрокового виконання основного циклу в припущенні, що використовується функція округлення, такі:

i	Plot	x	y
1	(-1, -1)	-0.5	-0.5
		-1.5	-1.0
2	(-2, -1)
		-2.5	-1.5
3	(-3, -2)
		-3.5	-2.0
4	(-4, -2)
		-4.5	-2.5
5	(-5, -3)
		-5.5	-3.0
6	(-6, -3)
		-6.5	-3.5
7	(-7, -4)
		-7.5	-4.0
8	(-8, -4)
		-8.5	-4.5

Попри те, що результати, наведені на рис. 7.2, виглядають цілком прийнятними, аналіз відрізків, проведених з точки (0, 0) в точку (-8, 4) і (8, -4), показує, що розкладений у растр відрізок лежить по одну сторону від реального і що на одному з кінців відрізка з'являється зайва точка. Тобто результат роботи алгоритму залежить від орієнтації. Отже, точність у кінцевих точках погіршується. Далі, якщо замість взяття цілої частини використовувати округлення до найближчого цілого, то результати знову вийдуть різними.

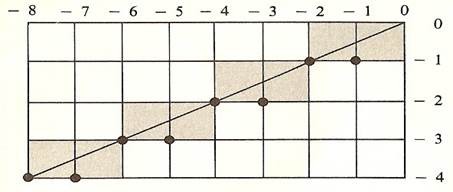
Рис. 7.2. Результати роботи простого ЦДА в третьому квадранті

Таким чином, або потрібно використовувати більш складний і більш повільний алгоритм, або потрібно відступитися від вимоги максимально точної апроксимації. До того ж запропонований алгоритм має той недолік, що описаний більш прийнятний алгоритм.