2. ПОХИБКИ ВИМІРЮВАННЯ
При вимірюванні фізичних величин за допомогою навіть найточніших засобів і методів їх результат завжди відрізняється від дійсного значення вимірюваної фізичної величини, тобто визначається з деякою похибкою. Визначення «похибка» є одним з центральних в метрології, в якому використовуються поняття «похибка результату вимірювання» і «похибка засобу вимірювання». Похибкою результату вимірювання називається відхилення результату вимірювання від істинного значення вимірюваної фізичної величини. Оскільки істинне значення вимірюваної величини невідоме, то при кількісній оцінці похибки користуються дійсним значенням величини. 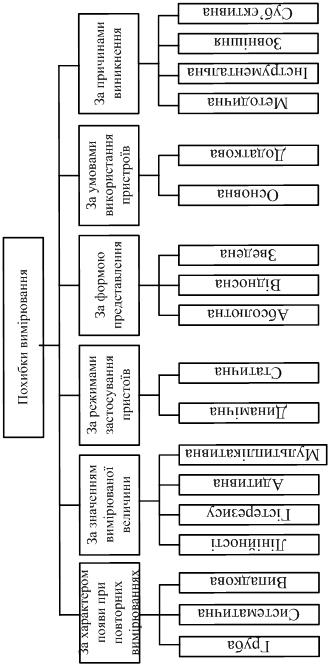
Рис.1.1. Похибки вимірювання Це значення знаходиться експериментальним шляхом і близьке до істинного значення, тому для поставленого вимірювального завдання може бути використане замість нього. Похибка засобу вимірювання (ЗВ) – різниця між показами ЗВ і дійсним (істинним) значенням вимірюваної фізичної величини. Вона характеризує точність результатів вимірювання, що проводяться даним засобом. Існує п'ять основних ознак, по яких класифікуються похибки вимірювання.1) По формі представлення (кількісного виразу) похибки діляться на абсолютні, відносні і зведені.Абсолютною похибкою Δ, вираженою в одиницях вимірюваної величини, називається відхилення результату вимірювання х від істинного значення хі :
Δ = x − хі
Абсолютна похибка характеризує величину і знак отриманої похибки, але не визначає якість самого проведеного вимірювання. Поняття похибки характеризує недосконалість вимірювання. Характеристикою якості вимірювання є поняття точності вимірювань, що відображає міру близькості результатів вимірювань до дійсного значення вимірюваної фізичної величини. Точність і похибка зв'язані зворотною залежністю. Інакше кажучи, високій точності вимірювань відповідає мала похибка. Тому, аби мати можливість порівнювати якість вимірювань, введено поняття відносної похибки.Відносною похибкою δ називається відношення абсолютної похибки вимірювання до дійсного значення вимірюваної величини:
δ = Δ / хі.
Похибку δ часто виражають в відсотках: δ = 100 Δ / хі (%). Оскільки зазвичай Δ << хі, то відносна похибка може бути визначена як δ ≈ Δ / x або δ = 100 Δ / x (%). Мірою точності вимірювань служить величина, зворотна модулю відносної похибки, тобто 1/|δ|. Якщо вимірювання виконане однократно і за абсолютну похибка результату вимірювання δ прийнята різниця між показом приладу і істинним значенням вимірюваної величини хі, то з співвідношення (1.2) виходить, що значення відносної похибки δ зменшується із зростанням величини хі. Тому для вимірювань доцільно вибирати такий прилад, покази якого були б в кінцевій частині його шкали (діапазону вимірювань), а для порівняння різних приладів використовувати поняття зведеної похибки. Зведеною похибкою γз, що виражає потенційну точність вимірювань, називається відношення абсолютної похибки Δ до деякого нормуючого значення XN (наприклад, до кінцевого значення шкали приладу або суми кінцевих значень шкал при двосторонній шкалі):γз = 100Δ / XN (%).
У вимірювальних
приладів, як правило, основна зведена похибка у всьому діапазоні вимірювань
нормується і називається класом точності приладу. Класи точності вибирають з
ряду: 1*10n ; 1.5*10n ; 2*10n ; 2.5*10n
; 4*10n ; 5*10n ; 6*10n, де n=1, 0, -1, -2,
-3, ... .
Максимальне
значення похибки приладу, при якому він допускається до використання
називається граничною допустимою похибкою і записується відповідно:
Δгр=±Δ, δгр=±δ
Тоді
інтервал дійсного значення вимірюваної величини записується у вигляді:
Хд = Х ± Δгр.
2) По характеру появи похибки вимірювань поділяються на систематичні, випадкові і грубі (промахи). Систематичні похибки Δc – складові похибки вимірювань, що залишаються постійними або закономірно змінюються при багатократних (повторних) вимірюваннях однієї і тієї ж величини в одних і тих же умовах. Такі похибки можуть бути виявлені шляхом детального аналізу можливих їх джерел і зменшені (застосуванням точніших приладів, калібруванням приладів і ін.). Проте повністю їх усунути не можна. По характеру зміни в часі систематичні похибки поділяються на постійні ( що зберігають в часі величину і знак), прогресуючі (що зростають або зменшуються в часі), періодичні, а також що змінюються в часі по складному неперіодичному закону. Основні з цих похибок – прогресуючі.Випадкові похибки Δв – складові похибки вимірювань, що змінюються випадковим чином при повторних (багатократних) вимірюваннях однієї і тієї ж величини в одних і тих же умовах. У появі таких похибок немає яких-небудь закономірностей, вони виявляються при повторних вимірюваннях однієї і тієї ж величини у вигляді деякого відхилення отримуваних результатів. Практично випадкові похибки неминучі, неусувні і завжди мають місце в результатах вимірювань. Опис випадкових похибок можливий лише на основі теорії випадкових процесів і математичної статистики.
На відміну від систематичних випадкові похибки не можна виключити з результатів вимірювань шляхом введення поправки, проте їх можна істотно зменшити шляхом багатократного вимірювання цієї величини і подальшою статистичною обробкою отриманих результатів.Грубі похибки (промахи) – похибки, що істотно перевищують очікувані результати. Такі похибки виникають через помилки оператора або невраховані зовнішні впливи.
Їх виявляють при обробці результатів вимірювань і виключають з розгляду, користуючись певними правилами.3) По причинах виникнення похибки вимірювання поділяються на методичні, інструментальні, зовнішні і суб'єктивні. Методичні похибки виникають зазвичай через недосконалості методу вимірювань, використання невірних теоретичних передумов (допущень) при вимірюваннях, а також через вплив вибраного засобу вимірювання на вимірювані фізичні величини. При підключенні електровимірювального приладу від джерела сигналу споживається деяка потужність. Це приводить до спотворення режиму роботи джерела сигналу і викликає похибку методу вимірювання (методичну), що розраховується за означенням для абсолютної і відносної похибок. Так, наприклад, якщо вольтметр має недостатньо високий вхідний опір, то його підключення до схеми здатне змінити в ній розподіл струмів і напруги. При цьому результат вимірювання може істотно відрізнятися від дійсного. Для розрахунку методичної похибки при вимірюванні струмів і напруги необхідно знати внутрішні опори амперметрів RA і вольтметрів RV . Якщо, наприклад, для вимірювання струму в деяке коло включити амперметр, причому вихідний опір кола по відношенню до затискачів амперметра рівний R, а напруга холостого ходу по відношенню до тих же затискачів U, то дійсне значення струму в ланцюзі (при RA = 0 ) визначаєтьсяIд = U / R
виміряне дорівнюєI = U /( R + RA ) .
Тоді абсолютна методична похибка дорівнює різниці дійсного значення струму і виміряного:ΔIМ = (I – Iд)
Відносна методична похибка при цьому рівнаδIМ= (I – Iд)/ Iд = − RA/( R + RA ).
Аналогічно для вимірювання напруги на затискачах активного двополюсника з вихідним опором R і напругою холостого ходу U використовувати вольтметр з внутрішнім опором RV, то для відносної методичної похибки вимірювання напруги можна аналогічно отриматиΔVМ =( UV − U ), δVМ =( UV − U )/ U = − R/ (R + RV)
де UV – напруга на затискачах вольтметра. Методичну похибка можна зменшити шляхом застосування точнішого методу вимірювання.Інструментальні (апаратурні, приладові) похибки виникають через недосконалості засобів вимірювання. Джерелами інструментальних похибок можуть бути, наприклад, неточне градуювання приладу і зсув нуля, варіація показів приладу в процесі експлуатації і так далі. Зменшують інструментальні похибки вживанням точнішого приладу.
Зовнішня похибка – важлива складова похибки вимірювання, пов'язана з відхиленням однієї або декількох впливаючих величин від нормальних значень або виходом їх за межі нормальної області (наприклад, вплив вологості, температури, зовнішніх електричних і магнітних полів, нестабільності джерел живлення, механічних дій і так далі). В більшості випадків зовнішні похибки є систематичними і визначаються додатковими похибками застосовуваних засобів вимірювань. Суб'єктивні похибки викликаються помилками оператора при відліку показів засобів вимірювання (похибки від недбалості оператора, від паралаксу, тобто від неправильного напряму погляду при відліку показів стрілочного приладу і ін.). Подібні похибки усуваються застосуванням сучасних цифрових приладів або автоматичних методів вимірювання.4) По характеру поведінка вимірюваної фізичної величини в процесі вимірювань розрізняє статичні і динамічні похибки. Статичні похибки виникають при вимірі сталого значення вимірюваної величини, тобто коли ця величина перестає змінюватися в часі.Динамічні похибки мають місце при динамічних вимірюваннях, коли вимірювана величина змінюється в часі і потрібно встановити закон її зміни. Причина появи динамічних похибок полягає в інерційності засобу вимірювання і визначається різницею похибки в динамічному режимі і статичної похибки.
5) За умовами, в яких використовуються засоби вимірювання, розрізняють основну і додаткову похибки. Засоби вимірювань можуть застосовуватися в нормальних і робочих умовах. Ці умови для конкретних видів ЗВ встановлені в стандартах або технічних умовах. Нормальним умови застосування засобів вимірювань є ряд основних вимог: температура довколишнього повітря (20±5) °С; відносна вологість (65±15) %; атмосферний тиск (100±4) кПа; напруга мережі живлення (220±4) В і (115±2,5) В; частота мережі (50±1) Гц і (400±12) Гц. Основна похибка вимірювального приладу має місце за нормальних умов експлуатації засобу вимірювання, обумовлених в регламентуючих документах (паспорті, технічних умовах і ін.). Її можна представити у вигляді суми похибок - адитивної і мультиплікативної.
Δ
= a+b*х ,
де а –
адитивна похибка – постійна при всіх значеннях х;
b –
мультиплікативна похибка – лінійно змінюється зі зміною х;
х –
поточне значення вимірювання;
Адитивна похибка – не залежить від чутливості
приладу і є постійною для всього діапазону вимірювань.
Мультиплікативна похибка – залежить від чутливості
приладу і змінюється пропорційно до поточного
значення вхідної величини.
Інтерпритація сказаного приведена на рис. 1.
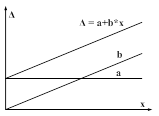
Рис 1.2. Адитивна і
мультиплікативна похибки ЗВ.
Додаткова похибка вимірювань виникає при відхиленні умов експлуатації ЗВ від нормальних (номінальних). Дана похибка, як і основна, вказується в нормативних документах. Необхідно відзначити, що проведена вище класифікація похибок вимірювань є умовною (відносною). Зокрема, при виготовленні вимірювальних мостів розкид опорів його резисторів можна віднести до випадкових похибок, тоді як в конкретному зібраному мосту цей розкид слід віднести до систематичних похибок вимірювального моста. Іншим прикладом може служити кліматична похибка вимірювального приладу. Якщо можливий контроль температури, при якій проводяться вимірювання, і є поправочна таблиця, то таку похибка слід розглядати як систематичну. Проте за відсутності контролю температур ця ж похибка враховується як випадкова.
Всі
похибки вимірювань містять в собі
систематичну і випадкову складові, що називаються також систематичною і
випадковою похибками.
При
вимірюванні ці похибки виявляються спільно, внаслідок чого сукупність
результатів вимірювання утворює нестаціонарний, випадковий процес.
Оскільки випадкові і систематичні похибки
при повторних вимірюваннях поводять себе неоднаково, відрізняються і методи їх
зменшення.
Методи зменшення систематичних похибок
Систематичними називають
похибки, які залишаються постійними або закономірно змінюються при повторних
вимірюваннях однієї і тієї ж величини.
Систематичні похибки поділяються на
постійні (наприклад, похибка зсуву нуля приладу) і змінні (наприклад, похибка,
обумовлена зміною температури середовища).
Для зменшення постійної систематичної
похибки найбільшого поширення набули наступні методи: введення поправок, метод
заміщення, метод компенсації похибки по знаку.
Введення
поправок є широко використовуваним методом виключення систематичних
похибок. Поправкою називають величину, яку треба додати до результату
вимірювання з метою виключення систематичної похибки. Поправки можуть бути
визначені різними способами: розрахунковим шляхом (наприклад, абсолютна
похибка, взята зі зворотнім знаком, поправки на методичні похибки), або за результатами
перевірки засобів вимірювань в робочих
умовах, що дає можливість врахувати всі систематичні похибки без з'ясування
причин їх виникнення.
Метод
заміщення є одним з найбільш поширених методів усунення більшості
систематичних похибок і полягає в тому, що дія на вимірювальний прилад
вимірюваної величини замінюється еквівалентною, відомою дією регульованої міри
на прилад. Вимірювання здійснюється в два етапи. При збереженні умов
експерименту похибка вимірювання визначатиметься похибкою міри і випадковою
похибкою вимірювального приладу. Метод заміщення широко використовується для
підвищення точності вимірювання величин, для яких існують точні регульовані
міри (наприклад, при вимірі опорів, ємкостей і ін.).
Метод компенсації похибки по знаку
застосовується для виключення відомих за природою, але невідомих за значенням
похибок, джерела яких мають направлену дію (похибки від впливу магнітних полів,
термоЕРС і ін.). Для усунення таких похибок
вимірювання проводять двічі (або парне число разів) так, щоб систематична
похибка входила в результати вимірювань
з протилежними знаками. Середнє значення з двох отриманих результатів є
остаточним результатом вимірювання.
Змінні систематичні похибки
залежать від зовнішніх дій, що постійно змінюються і значення яких зазвичай
невідомі, тому для їх зменшення використовуються методи, засновані на
використанні структурної і часової надмірності.
Метод
зразкових сигналів полягає в тому, що в процесі циклу вимірювань на вхід засобу вимірювань періодично замість вимірюваної величини Х
подаються зразкові сигнали Х01,
Х02 ..., Х0n. Процес вимірювання складається з n + 1
тактів. Спочатку вимірюють величину Х. У подальших тактах здійснюється
вимірювання зразкових сигналів, що по черзі підключаються через комутатор до
засобу вимірювання. Результати всіх вимірювань
Y0, Y01, Y02 ..., Y0n
утворюють систему рівнянь, з якої
знаходиться значення вимірюваної величини.
Метод допоміжних вимірювань використовується для виключення похибок від впливаючих величин і неінформативних параметрів
вимірюваного сигналу. Для реалізації цього методу одночасно з вимірюваною
величиною Х за допомогою допоміжних засобів вимірювань здійснюється вимірювання
кожної з впливаючих величин і обчислення за допомогою
обчислювального пристрою поправок до
результатів вимірювання. Метод можна застосувати для зниження впливу тих
дестабілізуючих чинників, які можуть бути легко враховані, але при цьому необхідно
знати залежність похибки засобу вимірювання від цих чинників.
Метод
симетричних спостережень застосовується для усунення прогресуючої
(мультиплікативної) систематичної похибки, що змінюється за лінійним законом в
часі. Він полягає в проведенні багатократних спостережень через рівні проміжки
часу з подальшим усередненням результатів вимірювань.
Метод періодичних вимірювань
застосовується в тому випадку, якщо впливаюча
величина, що створює систематичну похибка, змінюється по періодичному закону. В
цьому випадку два вимірювання проводять через половину періоду, коли похибка
має протилежні знаки, але рівні значення. В результаті усереднювання
результатів вимірювань систематична
похибка виключається.
Методи зменшення випадкових похибок
Випадковими
називаються похибки, що змінюються випадковим чином при повторних вимірюваннях
тієї ж величини. Випадкові похибки не можна заздалегідь виявити і усунути до і
в процесі вимірювання. Вони можуть бути зменшені при багатократних
спостереженнях однієї і тієї ж величини, фільтрацією похибок, застосуванням паралельних
вимірювань і ін. При цьому необхідно на основі певного ряду значень отримати
найкраще наближення вимірюваної величини до її істинного значення. Вимірювана
величина, що містить випадкову похибку, повинна розглядатися як випадкова
величина.
Випадкові похибки
Випадковими
називаються похибки, що змінюються випадковим чином при повторних вимірюваннях
тієї ж величини. Випадкові похибки не можна заздалегідь виявити і усунути до і
в процесі вимірювання. Вони можуть бути зменшені при багатократних спостереженнях
однієї і тієї ж величини, фільтрацією похибок і ін. При цьому необхідно на
основі певного ряду значень отримати найкраще наближення вимірюваної величини
до її істинного значення. Вимірювана величина, що містить випадкову похибку,
повинна розглядатися як випадкова величина.
Для
характеристики випадкового процесу визначають інтегральну і диференційну
функції розподілу імовірності випадкової величини.
Інтегральна
функція розподілу показує імовірність того, що випадкова
величина Х знаходиться в інтервалі
від - ∞ до деякого значення, меншого х1,
при функція є не спадаюча і F(-∞)=0, а F(+∞)=l.
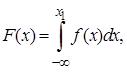
Диференційна
функція (густина імовірності) показує імовірність того, що
випадкова величина Х набуде значення
в інтервалі між x1 і x2, і рівна:
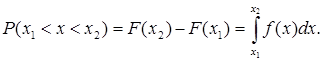
У практиці електровимірювань найчастіше мають справу з нормальним законом
розподілу. Випадкова величина Х
розподілена нормально, якщо її густина імовірності має вигляд:
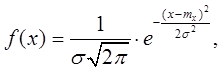
де σx
– середнє квадратичне відхилення (CКВ), mx – математичне очікування
випадкової величини. Функція показує розсіювання результатів навколо деякого
середнього значення, і повністю характеризується середнім квадратичним
відхиленням (рис. 2.б). Чим менше значення СКВ, тим частіше зустрічаються малі
випадкові похибки, тобто тим точніше виконані вимірювання.
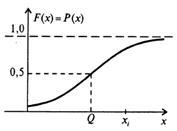
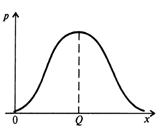
Рис 1.3. Інтегральна і диференційна функції нормального розподілу
імовірності результатів вимірювання.
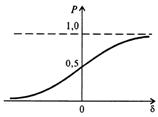
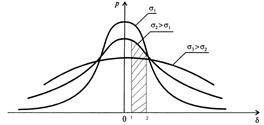
Рис 1.4. Інтегральна і диференційна функції нормального розподілу
імовірності похибок вимірювання.
Імовірність появи похибки в
інтервалі ![]() визначається площею
заштрихованої ділянки (рис 2.б) і визначається як визначений інтеграл від
функції (3) в межах (δ1, δ2). Інтеграл не
обчислюється в елементарних функціях, його обчислюють за допомогою таблиць
(таблиця 2.). Для спрощення запису здійснюють заміну змінних:
визначається площею
заштрихованої ділянки (рис 2.б) і визначається як визначений інтеграл від
функції (3) в межах (δ1, δ2). Інтеграл не
обчислюється в елементарних функціях, його обчислюють за допомогою таблиць
(таблиця 2.). Для спрощення запису здійснюють заміну змінних:
![]() , тоді
, тоді ![]() .
.
Тоді імовірність попадання
похибок в інтервал ![]() (або результатів
вимірювання в
(або результатів
вимірювання в ![]() ) обчислюється за
відомими значеннями t1 i t2 через табличні значення Ф1
і Ф2:
) обчислюється за
відомими значеннями t1 i t2 через табличні значення Ф1
і Ф2:
![]() .
.
Способи знаходження оцінок ряду
спостережень і показники їх якості залежать від законів розподілу. Для
нормального розподілу, як і для всіх симетричних розподілів, як оцінку
математичного очікування ряду n спостережень приймають середнє арифметичне ряду
спостережень, яке і приймають за дійсне значення вимірюваної величини ![]() .
.
 .
.
Величина δ = x – mx
є випадковою похибкою і може бути додатною і від’ємною. Якщо систематична
похибка відсутня, то математичне очікування дорівнює дійсному значенню xд.
Потім визначаються абсолютне
відхилення ![]() кожного результату
вимірювання відносно середнього значення (при чому виконується умова:
кожного результату
вимірювання відносно середнього значення (при чому виконується умова:
![]() ):
): ![]() .
.
Оцінка
відхилення результату спостереження від дійсного значення називається дисперсією
і обчислюється за формулою:
![]() .
.
Тоді середнє квадратичне
відхилення результатів n спостережень:
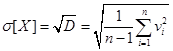 .
.
Середнє арифметичне залежить від числа спостережень і є
випадковою величиною, яка володіє деякою дисперсією відносно дійсного значення
величини Хд. Тоді оцінкою середнього квадратичного
для середнього арифметичного ряду спостережень відносно дійсного значення
(тобто відхилення ![]() при повторних вимірюваннях) є:
при повторних вимірюваннях) є:
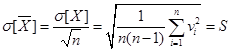 ,
,
S – середнє квадратичне
відхилення середнього арифметичного. Отже, збільшення кількості вимірювань n
веде до зменшення СКВ результату вимірювань.
Вимірювання з
багатократними спостереженнями і відповідна обробка результатів дозволяють
оцінити випадкову похибку і її зменшити. Оцінки ![]() і
і ![]() є так званими точковими оцінками випадкової похибки.
Вони вказують інтервал значень вимірюваної величини
є так званими точковими оцінками випадкової похибки.
Вони вказують інтервал значень вимірюваної величини ![]() , усередині якого знаходиться дійсне значення.
, усередині якого знаходиться дійсне значення.
На відміну від точкової при інтервальній оцінці визначається
довірчий інтервал εр, в якому з
довірчою імовірністю Р знаходиться дійсне значення Хд:
![]() .
.
При заданій імовірності Р і обчисленому ![]() значення
значення ![]() визначається законом
розподілу. В випадку нормального розподілу і числа вимірювань n>20 вибирається по таблиці функцій
Лапласа. Якщо число вимірювань n<20,
то довірчий інтервал випадкової величини визначається по формулі Стьюдента:
визначається законом
розподілу. В випадку нормального розподілу і числа вимірювань n>20 вибирається по таблиці функцій
Лапласа. Якщо число вимірювань n<20,
то довірчий інтервал випадкової величини визначається по формулі Стьюдента:
![]() ,
,
де ![]() – коефіцієнт розподілу
Стьюдента, який залежить від заданої імовірності Р і числа вимірювань n. При n>20 розподіл Стьюдента
наближається до нормального, і замість
– коефіцієнт розподілу
Стьюдента, який залежить від заданої імовірності Р і числа вимірювань n. При n>20 розподіл Стьюдента
наближається до нормального, і замість ![]() , можна використовувати
, можна використовувати ![]() для нормального
розподілу.
для нормального
розподілу.
Оскільки при рівномірному
розподілі довірчий інтервал слабо залежить від довірчої імовірності, зазвичай приймають
т![]() , тобто для P=1.
, тобто для P=1.
Таким чином результат вимірювання записується у вигляді ![]() , при Р = ..%
, при Р = ..%
Як правило, приймають Р=0,95. Якщо ж вимірювання не можна
повторити, то приймають Р=0,99, а в особливо відповідальних випадках ще вище.
Таблиця 1.
Таблиця коефіцієнтів Стьюдента.
|
n \ P |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
|
2 |
1,00 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
636,6 |
|
3 |
0,82 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
31,6 |
|
4 |
0,77 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
12,9 |
|
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
8,6 |
|
6 |
0,73 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
6,9 |
|
7 |
0,72 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
6,0 |
|
8 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
5,4 |
|
9 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
5,0 |
|
10 |
0,70 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
2,8 |
3,3 |
4,8 |
|
20 |
0,69 |
0,86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,9 |
3,9 |
|
40 |
0,68 |
0,85 |
1,1 |
1,3 |
1,7 |
2,0 |
2,4 |
2,7 |
3,6 |
|
60 |
0,68 |
0,85 |
1,0 |
1,3 |
1,7 |
2,0 |
2,4 |
2,7 |
3,5 |
|
∞ |
0,67 |
0,84 |
1,0 |
1,3 |
1,6 |
2,0 |
2,3 |
2,6 |
3,3 |
Таблиця 2.
Інтегральна функція нормованого нормального розподілу.![]()
|
t |
Ф(x) |
t |
Ф(x) |
t |
Ф(x) |
t |
Ф(x) |
|
-3,5 |
0,00023 |
-1,7 |
0,0446 |
+0,0 |
0,5000 |
+1,8 |
0,9641 |
|
-3,4 |
0,00034 |
-1,6 |
0,0548 |
+0,1 |
0,5398 |
+1,9 |
0,9713 |
|
-3,3 |
0,00048 |
-1,5 |
0,0558 |
+0,2 |
0,5793 |
+2,0 |
0,9773 |
|
-3,2 |
0,00069 |
-1,4 |
0,0808 |
+0,3 |
0,6179 |
+2,1 |
0,9821 |
|
-3,1 |
0,00097 |
-1,3 |
0,0968 |
+0,4 |
0,6554 |
+2,2 |
0,9861 |
|
-3,0 |
0,00135 |
-1,2 |
0,1151 |
+0,5 |
0,6915 |
+2,3 |
0,9893 |
|
-2,9 |
0,0019 |
-1,1 |
0,1357 |
+0,6 |
0,7157 |
+2,4 |
0,9918 |
|
-2,8 |
0,0026 |
-1,0 |
0,1587 |
+0,7 |
0,7580 |
+2,5 |
0,9938 |
|
-2,7 |
0,0035 |
-0,9 |
0,1841 |
+0,8 |
0,7881 |
+2,6 |
0,9953 |
|
-2,6 |
0,0047 |
-0,8 |
0,2119 |
+0,9 |
0,8159 |
+2,7 |
0,9965 |
|
-2,5 |
0,0062 |
-0,7 |
0,2420 |
+1,0 |
0,8413 |
+2,8 |
0,9974 |
|
-2,4 |
0,0082 |
-0,6 |
0,2743 |
+1,1 |
0,8643 |
+2,9 |
0,9981 |
|
-2,3 |
0,0107 |
-0,5 |
0,3085 |
+1,2 |
0,8849 |
+3,0 |
0,99865 |
|
-2,2 |
0,0139 |
-0,4 |
0,3440 |
+1,3 |
0,9032 |
+3,1 |
0,99903 |
|
-2,1 |
0,0179 |
-0,3 |
0,3821 |
+1,4 |
0,9192 |
+3,2 |
0,99931 |
|
-2,0 |
0,0228 |
-0,2 |
0,4207 |
+1,5 |
0,9332 |
+3,3 |
0,99952 |
|
-1,9 |
0,0287 |
-0,1 |
0,4602 |
+1,6 |
0,9452 |
+3,4 |
0,99966 |
|
-1,8 |
0,0359 |
-0,0 |
0,5000 |
+1,7 |
0,9554 |
+3,5 |
0,99977 |
Виключення грубих похибок.
В деяких випадках виявляється,
що результат одного вимірювання різко відрізняється від результатів інших
вимірювань, виконаних за тих же контрольованих умов. В цьому випадку говорять
про грубу похибку (промах). Причиною
можуть стати помилка оператора, поява значної короткочасної перешкоди, поштовх,
порушення електричного контакту і так далі. Такий результат, що містить грубу
похибку необхідно виявити, виключити і не враховувати при подальшій
статистичній обробці результатів вимірювань.
Згідно формули ![]() , для довірчого інтервалу
, для довірчого інтервалу ![]() , довірча імовірність рівна 0,9973. Тобто імовірність появи
похибки, більшої за 3σ рівна 1-0,9973=0,0027≈1/370. Така довірча
імовірність означає, що з 370 випадкових похибок тільки одна по абсолютному
значенню буде більша за 3σ. Тому 3σ вважається максимально можливою
випадковою похибкою, похибки більше 3σ вважаються грубими і при обробці
результатів вимірювань не враховуються.
, довірча імовірність рівна 0,9973. Тобто імовірність появи
похибки, більшої за 3σ рівна 1-0,9973=0,0027≈1/370. Така довірча
імовірність означає, що з 370 випадкових похибок тільки одна по абсолютному
значенню буде більша за 3σ. Тому 3σ вважається максимально можливою
випадковою похибкою, похибки більше 3σ вважаються грубими і при обробці
результатів вимірювань не враховуються.
Правила
додавання похибок прямих спостережень.
Випадкова похибка вимірювального пристрою ![]() , що складається з m блоків з випадковими похибками
, що складається з m блоків з випадковими похибками ![]() кожного блоку, знаходиться шляхом геометричного сумування:
кожного блоку, знаходиться шляхом геометричного сумування:
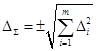
Аналогічно визначається відносна і граничні похибки, а також
середньоквадратичне відхилення. Систематичні похибки ![]() сумуються
з врахуванням їх знаків, сумарна похибка
сумуються
з врахуванням їх знаків, сумарна похибка ![]() є модулем отриманої
суми:
є модулем отриманої
суми:
![]() .
.
При наявності і випадкових і систематичних похибок загальна
похибка ![]() приймається рівною їх геометричній сумі:
приймається рівною їх геометричній сумі: ![]()
При наявності кореляційного зв’язку між випадковими похибками,
що характеризуються дисперсіями ![]() і
і ![]() , дисперсія суми цих величин:
, дисперсія суми цих величин:
![]()
Де ![]() - коефіцієнт кореляції між випадковими величинами, що служить
мірою лінійного зв’язку між двома випадковими величинами:
- коефіцієнт кореляції між випадковими величинами, що служить
мірою лінійного зв’язку між двома випадковими величинами:
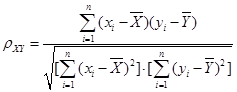
При ![]() > 0,6 (n>10) з великою імовірністю можна припустити, що
між величинами X і Y існує лінійний зв'язок.
> 0,6 (n>10) з великою імовірністю можна припустити, що
між величинами X і Y існує лінійний зв'язок.