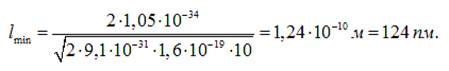Приклади розв’язування задач

Задача 1. Обчислити енергію фотона, що випромінюється при переході електрона у атомі з четвертого на другий енергетичний рівень.

Відповідно до серіальної формули для водневоподібних атомів:

,

енергія фотона випромінювання набуде вигляду:

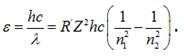
Врахуємо, що енергія іонізації атома гідрогену рівна:

Тоді енергію фотона запишемо:

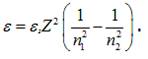
Підставивши значення відповідних фізичних величин одержимо:

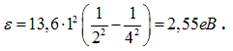
Задача 2. За теорією Бора визначити циклічну частоту та період обертання електрона в атомі гідрогену в основному стані.

1) Використаємо перший постулат Бора:

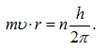
Враховуючи зв’язок лінійної та кутової швидкості, одержимо:

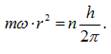
Підставимо в отриману формулу підставимо вираз для радіуса

n-ної орбіти електрона в атомі:

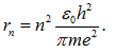
В результаті одержимо кінцеву робочу формулу:

Тоді:

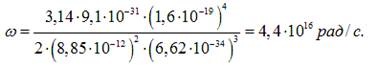
2) Для періоду обертання використаємо формулу:

Тоді:

Задача 3. Електрон без початкової швидкості пройшов прискорюючу різницю потенціалів. Визначити довжину хвилі де Бройля такого електрона для нерелятивістського та релятивістського випадків.

За означенням довжина хвилі де Бройля визначається:

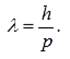
Запишемо формули для імпульс частинки.

1) Для нерелятивістського випадку:

2) Для релятивістського випадку:

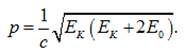
В даних формулах кінетична енергія визначається:

Енергія спокою:

.

Підставивши вищезгадані формули у вираз для довжини хвилі де Бройля отримаємо необхідний результат.

Задача 4. За співвідношенням невизначеності Гейзенберга оцінити розмір атома гідрогену при відомій кінетичній енергії його електрона.

За співвідношенням для координати та імпульсу:

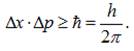
Якщо діаметр атома гідрогену позначити l, то невизначеність електрона в такому атомі можна записати:

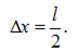
Співвідношення невизначеності набуде вигляду:

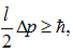
тоді:

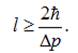
Врахуємо, що невизначеність імпульсу не перевищує самого імпульсу:

Використаємо співвідношення між імпульсом та кінетичною енергією:

Підставивши замість невизначеності імпульсу формулу для імпульсу, перейдемо від нерівності, у співвідношенні для невизначеності розміру, до рівняння:

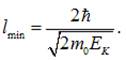
Обчислення дають наступний результат: