Лабораторна робота №12
Тема. Визначення
частотної оцінки якості САР методом одиничних трикутників і трапецій
Мета: ознайомитись з
частотним методом оцінки якості САР, оцінити якість системи методом одиничних
трикутників і трапецій
Розв’язання задачі автоматичного керування об’єктом
залежить не лише від стійкості системи автоматичного керування (САК), а й від
інших показників, які зазвичай об’єднують поняттям „якість системи керування”.
Це поняття застосовується виключно до стійких систем. Якість оцінюють за
кількома критеріями, основними з яких є: характер перехідного процесу, його
тривалість, перерегулювання, точність (похибка)
системи та інші показники, специфічні для певних типів перехідних процесів.
Частотні методи досліджування, які дістали найбільше
поширення на практиці, базуються на математичній залежності характеристики
перехідного процесу x(t) від дійсної
частотної характеристики замкнутої системи за збуренням 
.
Практично розгляд характеристики обмежується
зоною суттєвих частот 
.
Під зоною суттєвих частот розуміють зону зміни частоти
від 0 до , в якій виконується умова 
.
В зоні суттєвих частот виконується апроксимація
характеристики , яку замінюють рівнозначними фігурами 
- трапеціями і
трикутниками.
При заміні в зоні суттєвих
частот мають виконуватись такі правила:
1.
Прямолінійні частини
фігур мають по
можливості точно збігатися з кривою .
2.
Всі n фігур (трапеції і
трикутники) повинні мати однією зі своїх сторін вертикальну вісь.
3.
Алгебраїчна сума площ
всіх n фігур, якими замінюють характеристику має дорівнювати
площі, обмеженій характеристикою .
4.
Кількість фігур n має
бути по можливості менша.
Дослідимо перехідну
характеристику, замкненої САР за умови дії одиничного кидка навантаження 
. Для цього, скористаємося одним із частотних методів – методом одиничних
трапецій, та трикутників, який дає можливість дістати відповіді на основні
питання, якості про характер перехідного процесу, його тривалість, величину перерегулювання. Частотні методи досліджування базуються,
на математичній залежності характеристики, перехідного процесу 
від
дійсної частотної характеристики замкнутої системи за збуренням.
Приклад.
Насамперед згідно алгоритму, вибраного методу побудуємо залежність, дійсної
частини 
амплітудно-фазової частотної, характеристики замкнутої
системи за збуренням від частот 
.
Передаточна функція замкненої, системи за збуренням 
по завданню має вигляд:
Зробимо заміну 
:
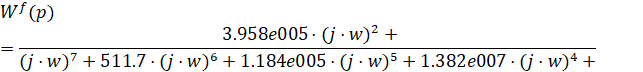
Згідно схеми типових перетворень, якщо :
(1)
то дійсні та уявні частини від 
визначаються
як:
Отже, дійсна частина
амплітудно-фазової частотної характеристики матиме вигляд:
Замінюючи ω від 0 до ωс,
де ωс – границя зони суттєвих частот,
(тобто таких ,для яких виконується умова 
), отримуємо характеристику U(ω) (рис. 1).
Границя зони суттєвих частот в нашому випадку буде дорівнювати 13.3 при частоті 4.0с-1 .
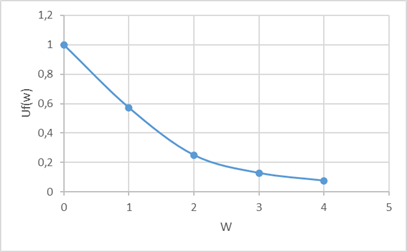
Рисунок 1 – Дійсна частина
амплітудно-фазової частотної характеристики
Отриману характеристику апроксимуємо рівнозначними
фігурами . В нашому
випадку це 1 трапеції і 1 трикутник
(рис.2):
1 – трикутник
АВС; 2 – трапеція ВСDЕ.
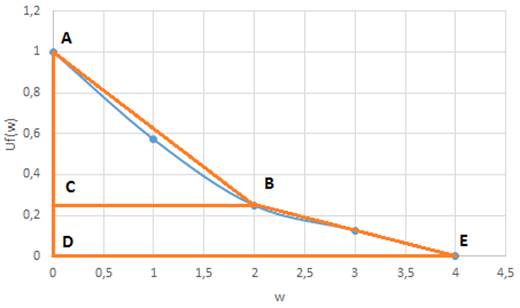
Рисунок 2 – Апроксимуючі
еквівалентні фігури
З рис. 2 визначаємо
висоти 
та нахили фігур
:
– трикутник ABC; H1p=0.750648; ω11p=2;
– трапеція ВСDE; H2p=0.249352; ω02p=2;
ω12p=4; ν2p=2/4=0,5;
За даними таблиць h-функцій по відповідних значеннях 
знайдемо відповідні значення h-функцій для
фігур H2 –H1
Помноживши знайдені табличні значення 
на ординати відповідних фігур 
, отримуємо ординати 
відповідних фігур. Знайдемо результуючі
перехідні характеристики при різних 
.
Отримавши ординати перехідного процесу при різних
значеннях реального часу побудуємо відповідну характеристику (рис.3):
Всі дані для оцінки САР занесено в
таблицю 1.
Таблиця 1 – Дані для оцінки якості САК
|
t |
h1(t) |
h2(t) |
x1(t) |
x2(t) |
Ʃx(t) |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0,896 |
0,9949 |
0,672580243 |
0,24808071 |
0,920660953 |
|
10 |
0,939 |
1,0008 |
0,704933154 |
0,249551889 |
0,954485044 |
|
15 |
0,956 |
0,9994 |
0,717619098 |
0,249202796 |
0,966821894 |
|
20 |
0,967 |
1,0005 |
0,726101416 |
0,249477084 |
0,9755785 |
|
25 |
0,975 |
1 |
0,732031532 |
0,249352408 |
0,98138394 |
|
30 |
0,980 |
0,9999 |
0,735634641 |
0,249327472 |
0,984962113 |
|
35 |
0,983 |
1 |
0,73751126 |
0,249352408 |
0,986863667 |
|
40 |
0,984 |
0,9999 |
0,738862425 |
0,249327472 |
0,988189898 |
|
45 |
0,986 |
1,0001 |
0,740213591 |
0,249377343 |
0,989590934 |
|
50 |
0,988 |
1 |
0,741489692 |
0,249352408 |
0,990842099 |
|
55 |
0,989 |
1 |
0,742465534 |
0,249352408 |
0,991817941 |
|
60 |
0,990 |
1 |
0,743066052 |
0,249352408 |
0,992418459 |
|
65 |
0,991 |
1 |
0,743591505 |
0,249352408 |
0,992943913 |
|
70 |
0,991 |
1 |
0,744116958 |
0,249352408 |
0,993469366 |
|
75 |
0,992 |
1 |
0,744717476 |
0,249352408 |
0,994069884 |
|
80 |
0,993 |
1 |
0,7450928 |
0,249352408 |
0,994445208 |
|
85 |
0,993 |
1 |
0,745693318 |
0,249352408 |
0,995045726 |
|
90 |
0,993 |
1 |
0,745693318 |
0,249352408 |
0,995045726 |
|
95 |
0,993 |
1 |
0,745693318 |
0,249352408 |
0,995045726 |
|
100 |
0,993 |
1 |
0,745693318 |
0,249352408 |
0,995045726 |
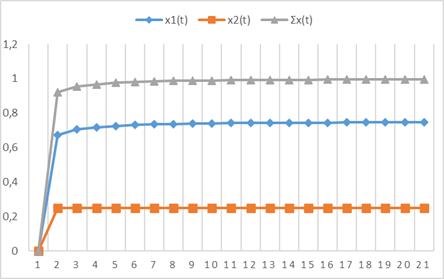
Рисунок
3 – Перехідний процес САР
Проведемо
аналіз отриманої перехідної характеристики. Виходячи з рис. 3 можемо визначити
основні показники якості:
1)
Перерегулювання системи σ=0%.
2)
Час регулювання складає 85 с
3)
Процес є монотонним.
Завдання для виконання
1.
Побудувати
перехідну характеристику САР та визначити показники якості, характер процесу та
час регулювання.
2.
Дані в таблиці
відповідно до порядкового номеру в журналі.
Дослідити САР,
яка описана такими передаточними функціями:
1.Об’єкт керування:
(без збурення)
(зі збуренням)
2.Вимірювальний елемент:
3.Керуючий елемент:
4.Виконуючий елемент:
Таблиця 1 – Параметри розрахунку САР
|
Варіант |
To, °C |
k₀, °C/рад |
kf |
Tд, |
kд, В/°C |
Tм, с |
Tя, с |
ky |
f, °C |
kφ, рад/(В·с) |
|
1 |
2 |
50 |
0,3 |
2 |
0,015 |
0,015 |
0,002 |
50 |
-10 |
0,05 |
|
2 |
1,8 |
45 |
0,4 |
1,5 |
0,015 |
0,016 |
0,005 |
60 |
15 |
0,05 |
|
3 |
1,4 |
40 |
0,5 |
3 |
0,015 |
0,018 |
0,003 |
70 |
-20 |
0,05 |
|
4 |
1,1 |
30 |
0,3 |
2,5 |
0,015 |
0,02 |
0,004 |
80 |
12 |
0,05 |
|
5 |
1 |
55 |
0,45 |
4 |
0,015 |
0,015 |
0,005 |
90 |
-14 |
0,05 |
|
6 |
1,3 |
60 |
0,28 |
1,3 |
0,015 |
0,018 |
0,002 |
100 |
20 |
0,05 |
|
7 |
0,8 |
45 |
0,5 |
1,1 |
0,015 |
0,02 |
0,003 |
80 |
-10 |
0,05 |
|
8 |
0,9 |
38 |
0,4 |
1,7 |
0,015 |
0,01 |
0,004 |
85 |
15 |
0,05 |
|
9 |
1,4 |
50 |
0,3 |
1,8 |
0,015 |
0,012 |
0,005 |
70 |
-20 |
0,05 |
|
10 |
1,7 |
55 |
0,45 |
1,9 |
0,015 |
0,014 |
0,002 |
75 |
10 |
0,05 |