2.11. Циліндричні зубчасті передачі
Параметри початкового контуру. Згідно
з діючими стандартами параметри початкового контуру для циліндричних прямо- та
косозубих передач регламентовані такими значеннями (для зубчастих коліс із
модулем т ≥
hf* = h*a + c* = 1,25,
радіуса кривини перехідної кривої ρf * = 0,38.
Розміри зубців та вінців
зубчастих коліс.
Основною
відмінністю косозубих коліс у порівнянні з прямозубими є те, що у косозубих
лінія зубців нахилена під деяким кутом β до твірної ділильного циліндра
(рис. 18, а). Різновидністю
косозубих коліс є шевронні зубчасті колеса (рис. 18, б). Шевронне зубчасте
колесо складається як би з двох косозубих коліс, суміщених торцями так, щоб
зубці мали протилежний нахил. Косозубі колеса використовують із кутом нахилу
зубців β = 8...20°, а у шевронних колесах беруть β = 20...40°,
кут нахилу зубців прямозубих коліс β= 0.
Зважаючи
на те, що косозубі (шевронні) зубчасті колеса можуть нарізуватись таким самим
стандартним інструментом, як і
прямозубі, кут профілю зубців косозубих (шевронних) коліс у їх нормальному
перерізі
αn = α = 20° (відповідно до початкового контуру).
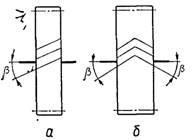
Рис. 18. Розміщення зубців на косозубому та шевронному колесах
За стандартний модуль зубців косозубих
(шевронних) коліс беруть модуль mn
також у нормальному перерізі зубців. У прямозубих колесах нормальний та
коловий модулі однакові: т = тп = mt.
Згідно
зі значеннями параметрів стандартного початкового контуру розміри зубців
циліндричних зубчастих коліс визначають за формулами, наведеними у табл. 1.
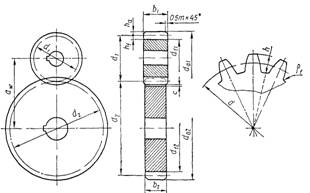
Рис. 19. Параметри циліндричної зубчастої
передачі
Формули для розмірів вінців циліндричних
зубчастих коліс із числами зубців z1 і z2, що утворюють
зубчасту передачу згідно з рис. 52, наведені у табл. 2.
Таблиця 1. Розміри
елементів зубців циліндричних зубчатих коліс
|
Елементи зубця |
Колесо |
|
|
прямозубе |
косозубе
(шевронне) |
|
|
Висота: головки ніжки зубця Радіальний зазор Радіус кривини перехідної кривої |
ha – h"а ·m = m hf = (h*+c*) · m = 1,25m h = ha + hf = 2,25m с = c* · m = 0,25m pf = pf* · m = 0,38m |
ha = ha* · mn = mn hf =( ha* + c*)· mn= l,25mn h = ha + hf = 2,25mn c = c* · mn = 0,25mn pf = pf* · mn = 0,38mn |
Таблиця 2. Розміри вінців пари циліндричних зубчастих коліс
|
Діаметри вінців |
Передача |
|
|
прямозуба |
косозуба (шевронна) |
|
|
Ділильні Вершин зубців Впадин |
d1 = m · z1; d2 = m · z2 da1 = d1
+ 2ha = d1 + 2m, da2 = d2 + 2ha = d2
+ 2m; df1 = d1
–
2hf = dl – 2,5m; df2 = d2
– 2hf = d2 – 2,5m |
d1 = mn ·z1/cosβ; d2 = mn ·z2/cosβ da1 = d1 + 2ha = d1 + 2mn; da2 = d2 + 2ha = d1
+ 2mn; df1 = d1
–
2hf = d1 – 2,5mn; df2 = d2
–
2hf = d2 – 2,5mn |
Міжосьова відстань циліндричних зубчастих передач:
– прямозубої:
аω = 0,5 ·
(d1 + d2 )= 0,5m · (zl + z2); (46)
– косозубої або (шевронної):
aω = 0,5mn · (z1 + z2)
/ cos β. (47)
Враховуючи
те, що передаточне число зубчастої
передачі u = z2
/ z1 , ділильні діаметри зубчастих коліс (у некоригованих
передачах початкові збігаються з ділильними) можуть бути виражені через
міжосьову відстань:
d1 = 2aω / (u ± 1); d2
= 2aω · u / (u
± 1). (48)
Тут
знак плюс – для передачі зовнішнього зачеплення; знак мінус – для передачі
внутрішнього зачеплення.
Ширину зубчастого вінця b2 колеса потрібно
брати залежно від міжосьової відстані передачі:
b2 = ψba ·
aω , (49)
де ψba – коєфіцієнт
ширини вінця, який беруть: ψba = 0,1...0,4 –для прямозубих передач,
ψba = 0,2...0,5
– для косозубих та ψba
= 0, 4...0,8 – для шевронних передач. Менші значення ψba вживають при несиметричному
або консольному розміщенні зубчастого колеса щодо опор вала, а також при
твердості зубчастих коліс Н >
350 НВ.
Граничні
значення ψba
повинні бути такими, щоб виконувались умови:
ψba = b2 / d1= 0,5
ψba (u + 1) ≤ 1 – для прямозубих передач,
ψba ≤ 1,5 – для косозубих передач,
ψba ≤ 2,5
– для шевронних зубчастих передач.
Ширину
зубчастого вінця шестірні b1 беруть на 2 –
Коефіцієнти
торцевого та осьового перекриття. Загальний
коефіцієнт перекриття зубчастої передачі:
εγ =εα + εβ, (50)
де
εα і εβ
– коефіцієнти торцевого та осьового
перекриття зубців відповідно.
Для зубчастих передач без модифікації зубців
і з некоригованими зубцями коефіцієнт торцевого перекриття можна
визначити за такою наближеною залежністю:
εα = [1,88 – 3,2 · (1/z1
± 1/z2,)] соs β.
(51)
Тут знак плюс для передач зовнішнього, а знак
мінус – внутрішнього зачеплення. У прямозубих передачах (β= 0)
рекомендують εα ≥ 1,2, а у косозубих:
(β ≠ 0) – εα
≥ 1.
Коефіцієнт осьового перекриття
εβ виражається відношенням ширини зубчастого вінця колеса b2 до осьового
кроку зубців Рх:
εβ = b2 / Рх = b2 · sin β / Рn = (b2 · sin β)/(π · mn). (52)
У прямозубих зубчастих передачах εβ
= 0, а у косозубих передачах рекомендують брати εβ ≥
1,1, що досягається вибором ширини вінця Ь2
при заданих β та mn.
Заміна косозубих зубчастих коліс
еквівалентними прямозубими.
Міцність
зубця визначають його розміри та форма у нормальному перерізі. Форму косого
зубця у нормальному перерізі визначають через параметри еквівалентного
прямозубого колеса (рис. 20).
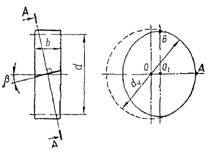
Рис. 20. До питання заміни косозубого колеса еквівалентним прямозубим
Нормальний
до зубця переріз зубчастого колеса має форму еліпса з півосями:
O1 · A = 0,5 · d;
О1 · В =
0,5 · d/cos β.
Максимальний
радіус кривини еліпса:
О · А = (О1 · В)2
/ (O1 · A) = d/(2 ·
cos2 β).
Радіус
еквівалентного прямозубого колеса беруть рівним максимальному радіусу кривини
еліпса, тобто діаметр dυ
еквівалентного прямозубого колеса визначають за формулою:
dυ = d/cos2 β. (53)
Ширина
вінця еквівалентного прямозубого колеса дорівнює ширині вінця косозубого
колеса, тобто bυ = b,
а його модуль тν дорівнює нормальному модулю тп
косозубого колеса.
Число
зубців еквівалентного прямозубого колеса знаходять на основі співвідношення dυ = mn ·
zυ = mn ·z/cos3 β, звідки
дістаємо
zυ = z/соs3β. (54)
Заміна
косозубих зубчастих коліс еквівалентними прямозубими використовується у
розрахунках на міцність зубців зубчастих передач.
Радіуси кривини профілів зубців та приведена
їхня кривина
У
розрахунках зубців зубчастих коліс на контактну втому використовують зведену
кривину профілів зубців у їхньому нормальному перерізі, коли точка контакту
профілів знаходиться у полюсі зачеплення.
Для
прямозубої передачі (рис. 21, а) радіуси кривини профілів зубців у полюсі
зачеплення визначають за такими формулами:
ρ1 = a1· P
= 0,5·d1· sin α t ω ;
ρ2 = a2·
P = 0,5·d2· sin
α t ω , (55)
де
α t ω – кут зачеплення, який у некоригованих
зубчастих колесах дорівнює ділильному
куту профілю зубців (α t ω = α = 20°).
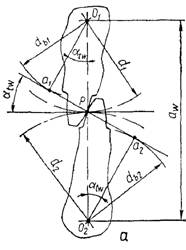
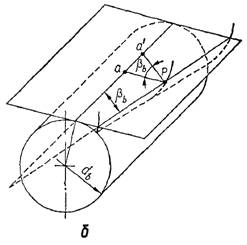
Рис. 21. До визначення радіусів кривини профілів зубців
У
косозубому зубчастому колесі радіус кривини профілю у нормальному перерізі
зубця (рис. 21, б):
ρn = a’ · P = (a · P) / cos β b
= ρ / cos β b
Відповідно
для косозубих шестірні та колеса з урахуванням залежностей (55) маємо для
нормального перерізу зубців:
ρn1 = 0,5d1 · sin αn/cos β b; ρn2= 0,5d2 · sin
αn/cos β b,
(56)
де β b – кут нахилу лінії
зубців на основному циліндрі діаметром db.
У точці контакту зубців зведена кривина їхніх профілів:
1/ρзв
= 1/ρn1 ± 1/ρn2 = 2cos β b /d1sin
αn ± 2 cos β b / d2 sin αn
=
= 2
cos β b / sin αn (1/d1 ± 1/d2).
Якщо
d2 = ud1, то остаточно запишемо:
1/ρзв = [2 cos β b ·(d1 · sin
αn)] (u ± 1)/ u.
Тут
знак плюс – для передач зовнішнього зачеплення; знак мінус – для передач
внутрішнього зачеплення.
Сумарна
довжина ліній контакту зубців у зачепленні. Сумарна довжина контактних ліній lΣ
зубців, що одночасно знаходяться у зачепленні, залежить від значення
коефіцієнтів торцевого εα та осьового εβ
перекриття. В прямозубих передачах lΣ різко змінюється при
переспряженні зубців (рис. 22, а, б).
Здебільшого 1 < εα < 2 і сумарна довжина контактних
ліній у період однопарного зачеплення (рис. 22, а) буде lΣ = b, а у період двопарного зачеплення lΣ = 2 b (рис. 22, б). У косозубих передачах (рис.
22, в) сумарна довжина
контакту: lΣ = b
εα / cosβ.
Якщо
εα або εβ – ціле число, то lΣ
у косозубій передачі не змінюється, оскільки зменшення довжини контакту зубця 1
(рис. 22, в) відповідає такому
ж збільшенню довжини контакту зубця 3 при
незмінній довжині контакту зубця 2.
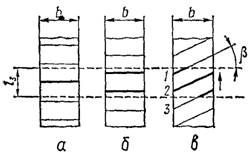
Рис. 22. До визначення сумарної довжини ліній контакту зубців у зачепленні
У загальному випадку εα і
εβ не цілі числа
і lΣ коливається у деяких межах. Тому
рекомендується сумарну довжину ліній контакту зубців визначати за формулою
lΣ =Кε · b · εα / cos β,
де Кε – коефіцієнт, що враховує коливання
сумарної довжини ліній контакту зубців.
Для
розповсюджених на практиці зачеплень величина Кε змінюється в межах 0,9–1,0. У середньому
можна брати Кε
= 0,95.
Найвигіднішим
для роботи зубчастої передачі є випадок lΣ = const. Цього можна
досягнути відповідним вибором β та ширини зубчастого вінця b так, щоб коефіцієнт осьового
перекриття εβ був цілим числом.
Навантаження на зубці циліндричних зубчастих
передач
Номінальні
сили у зачепленні циліндричних коліс. У навантаженій зубчастій передачі сила
взаємодії зубців розподілена вздовж їхнього контакту. Цю розподілену силу
замінимо зосередженою силою, прикладеною до зубця у середньому нормальному
його перерізі. Силами тертя, що виникають у результаті ковзання профілів
зубців, можна знехтувати, оскільки коефіцієнт тертя в зоні контакту малий, і
тому таке припущення не впливає практично на кінцевий результат.
На
рис. 23, а показане косозубе
зубчасте колесо, яке навантажене обертовим моментом Т1. Зубці цього
колеса взаємодіють із зубцями спареного зубчастого колеса. Схема взаємодії
зубців показана у їх середньому нормальному перерізі А–А.
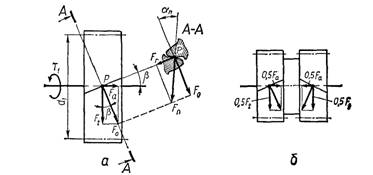
Рис. 23. Зусилля на зубці циліндричних зубчастих коліс
Сила
Fn направлена
вздовж нормалі до профілів зубців у точці їх контакту,
тобто вздовж лінії зачеплення, яка утворює кут зачеплення αn
із перпендикуляром до лінії центрів коліс. Силу Fn замінимо двома її взаємно перпендикулярними
складовими Fr і F0,
які перенесемо на схему колеса. Тут сила Fr
проекціюється у точку Р, а сила
F0 направлена перпендикулярно до лінії зубця. Тепер силу F0 також замінимо двома її взаємно
перпендикулярними складовими Ft і Fa.
Отже,
замість однієї нормальної сили Fn
на зубець маємо три взаємно перпендикулярні її складові Ft, Fa і Fr, Таке зображення
сил, що діють на зубці у зачепленні, зручне для розрахунків зубчастої передачі,
її валів та їхніх опор.
Сила
Ft , яку
будемо називати коловою силою,
лежить у площині дії обертового моменту Т1 і направлена по
дотичній до ділильного кола зубчастого колеса. Тому:
Ft = 2Т1/d1.
(57)
Складова
Fa, яка перпендикулярна
до площини колеса і паралельна осі його вала, називається осьовою силою. Вона
може бути виражена через Ft
та кут нахилу зубців β
Fa = Ft
tgβ.
(58)
Сила Fr діє у площині колеса і
направлена вздовж його радіуса, тому її називають радіальною силою. Для визначення Fr попередньо
знайдемо
F0 = Ft
/cos β,
а тоді (див. переріз А–А на рис. 23)
запишемо:
Fr = F0· tg
αn = Ft ·
tg αn /cosβ. (59)
Нормальна
сила Fn до
профілів зубців дорівнює геометричній сумі сил Ft, Fa і Fr.
Модуль
цієї сили можна визначити за формулою:
Fn = F0/cos
αn = Ft
/ (cosαn· cos β), або Fn = 2T1/(d1 cosαn
· cos β). (60)
У
разі зачеплення прямозубих коліс (β = 0) колова сила також визначається
за формулою Ft = 2Т1/d1,
осьова сила Fа =
0, а радіальна сила може бути знайдена за формулою:
Fr = Ft· tgα. (61)
Наявність осьової сили Fa у зачепленні косозубих коліс, що додатково
навантажує вали та їхні опори, обмежує використання косозубих коліс із великим
кутом нахилу лінії зубців β (Fа
зростає із збільшенням β). Цього недоліку позбавлені шевронні
зубчасті передачі, де осьові сили у зачепленні взаємно зрівноважуються, бо лівий та правий півшеврони мають
протилежний нахил зубців. Цим пояснюється можливість збільшення кутів нахилу
зубців у шевронних колесах у порівнянні з косозубими. Колова та радіальна сили
у зачепленні шевронних зубчастих коліс визначаються відповідно за формулами: Ft
= 2Т1/d1 і
Fr = F0 ·
tg αn = = Ft
· tg βn /cosβ.
Розрахункове
навантаження на зубці зубчастої передачі. За розрахункове навантаження на
зубці беруть максимальне значення питомого навантаження, розподіленого вдовж
лінії контакту зубців у їхньому зачепленні:
q = (Fn/lΣ) · Kα · Кβ · Кν = [Ft/(b · Кε · εα
/ cosαn)] · Kα
· Кβ ·
Кν. (62)
Тут Fn та lΣ
вибрані згідно з формулами (18) і (14), KαКβ
– коефіцієнти, що враховують розподіл навантаження між зубцями та
за шириною зубчастих вінців коліс відповідно; Кν – коефіцієнт, що враховує динамічне
навантаження зубців.
Коефіцієнти
KαКβ
і Кν різні у
розрахунках зубців на контактну втому і на втому при згині. Тому вводять такі
позначення коефіцієнтів: КHα,
КHβ, KHv – у розрахунках на контактну втому;
КFα, КFβ,
KFv
– у розрахунках зубців на згин.
Додатково
введемо поняття питомої розрахункової колової сили:
WH t
= (FHt / b) · КHα,
КHβ, KHv , WF t = (FFt / b) · КFα, КFβ,
KFv . (63)
На
основі виразу (62) розрахункове навантаження на зубці буде визначатись за
такими формулами:
– при розрахунках зубців на контактну
витривалість:
qн = WH t /( Кε·
εα / cosαn); (64)
– при розрахунках зубців на втому при згині:
qF = WF t /( Кε·
εα / cosαn). (65)
Колові
сили FHt і FFt У виразах (63)
знаходять згідно з формулою (15):
FHt = 2T1H/d1, FFt = 2T1F/d1. (66)
Взагалі
беруть обертові моменти T1H
= T1F такими, що дорівнюють максимальному тривало діючому
обертовому моменту T1 відповідно до заданого типового режиму
навантаження передачі (див. 2.2).
Розподіл
навантаження між зубцями. У прямозубих зубчастих передачах та косозубих при
εβ≤1 навантаження у зачепленні може передаватись
однією парою зубців. Тому для таких передач коефіцієнт, що враховує розподіл
навантаження між зубцями, рекомендують брати КHα=КFα=1.
У
косозубих та шевронних зубчастих передачах у зачепленні одночасно знаходяться
кілька пар зубців. Через похибки кроків та напрямів нахилу зубців окремі пари
контактуючих зубців навантажуються нерівномірно. Цю нерівномірність враховують
відповідними значеннями коефіцієнтів КHα
і КFα. Для косозубих та шевронних
зубчастих передач значення КHα,
наведені у табл. 3, а КFα
можна визначити за формулою:
КFα = [4 + (εα – 1) · (nCT
– 5)] / (4εα), (67)
де nCT – ступінь точності за нормою контакту зубців. Якщо nCT
> 9, то беруть nCT = 9 і аналогічно, якщо nCT < 5, то nCT = 5.
|
Таблиця 3. Коефіцієнт КHα
для косозубих та шевронних передач |
|||||
|
Колова
швидкість коліс v,
м/с |
Значення
КHα для ступеня
точності за нормами плавності |
||||
|
5 |
6 |
7 |
8 |
9 |
|
|
2,5 |
1 |
1,01 |
1,03 |
1,05 |
1,13 |
|
5 |
1 |
1,02 |
1,05 |
1,09 |
1,16 |
|
10 |
1,01 |
1,03 |
1,07 |
1,13 |
|
|
15 |
1,01 |
1,04 |
1,09 |
– |
– |
|
20 |
1,02 |
1,05 |
1,12 |
– |
– |
|
25 |
1,02 |
1,06 |
– |
– |
– |
Розподіл
навантаження по ширині зубчастих вінців. Навантаження по ширині вінця зубчастих
коліс розподіляється рівномірно тільки при ідеально точному виготовленні та
монтажі передачі, а також при абсолютно жорстких валах та їхніх опорах. У
реальних передачах при їхньому навантаженні зубчасті колеса перекошуються одне
відносно одного (рис. 24, а).
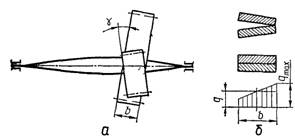
Рис. 24. До
питання концентрації навантаження по ширині зубчастих коліс
У
результаті деформацій валів та опор і похибок виготовлення та монтажу передачі
із абсолютно жорсткими зубцями мали б кутове дотикання зубців, як показано на
рис. 24, б. Через податливість
зубців їх контакт відбувається на всій або на значній частині ширини зубчастого
вінця. Однак пружні деформації зубців по їх довжині неоднакові і відповідно
навантаження у контакті розподіляється нерівномірно (див. епюру q на рис. 24, б).
Нерівномірність
навантаження по ширині вінця b враховується
коефіцієнтом Kβ, що дорівнює відношенню максимального питомого
навантаження qmax до
його номінального значення q.
Зубці
зубчастих коліс можуть припрацьовуватись, через що розподіл навантаження може
частково або майже повністю вирівнюватися. Здатність до припрацювання зубців
залежить від матеріалів зубчастих коліс та умов їхньої роботи.
Вважають,
що зубці передачі припрацьовуються, якщо матеріал хоч би одного з коліс має
твердість Н ≤ 350 НВ, а
колова швидкість коліс ν ≤
15 м/с. При твердості зубців Н > 350
НВ і коловій швидкості v >
15 м/с зубці слабо припрацьовуються або не припрацьовуються зовсім. При
швидкості
v > 15 м/с систематичне спрацьовування зубців відсутнє незалежно від
матеріалів коліс, бо між зубцями утворюється стійка масляна плівка достатньої
товщини.
Повне
припрацювання зубців у передачах можливе не завжди, а тільки при постійному
навантаженні передачі. Це пов’язано із закручуванням валів та самого тіла
шестірні. При змінному навантаженні досягається часткове припрацювання зубців і
нерівномірність розподілу питомого тиску у контакті зменшується в недостатній
мірі.
Отже,
основними факторами, що обумовлюють нерівномірність розподілу навантаження по
ширині зубчастих вінців, є: податливість валів та їхніх опор; похибки
виготовлення зубчастих коліс та монтажу передачі; розміщення зубчастих коліс на
валах відносно опор; умови, за яких не відбувається припрацювання зубців
(висока твердість зубців, висока колова швидкість та несталість навантаження
передачі). За інших рівних умов нерівномірність розподілу навантаження тим
вища, чим більша ширина зубчастого вінця, яка характеризується коефіцієнтом
ψbd = b/d1.
Для
наближеної оцінки коефіцієнта Kβ рекомендують графіки, складені
на основі розрахунків та практики експлуатації зубчастих передач. Графіки
рекомендують для передач, жорсткість та точність деталей яких задовольняють
нормам редукторобудування.
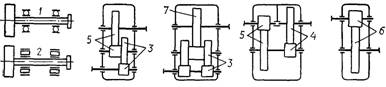
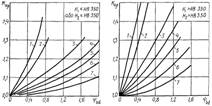
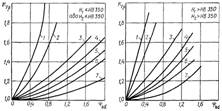
Рис. 25. Графіки для визначення коефіцієнтів KHβ і KFβ
Явище
нерівномірності розподілу навантаження по ширині вінців зубчастих коліс
неоднаково впливає на контактну міцність активних поверхонь зубців та міцність
зубців при згині. Тому за даними на рис. 25 графіками окремо вибирають
коефіцієнти КHβ
і КFβ, які використовуються у
відповідних розрахунках зубчастих передач. Криві 1–7 на графіках відповідають
різним випадкам розміщення коліс 1–7 щодо опор валів, а вплив ширини зубчастого
вінця враховується коефіцієнтом ψbd. Графіки розроблені для
різних твердостей зубців і для наявних на практиці змінних режимів
навантаження передач при коловій швидкості коліс v < 15 м/с. При постійному навантаженні, твердості
одного з коліс передачі Н <
350 НВ і швидкості v < 15
м/с можна брати КHβ
= КFβ =
1.
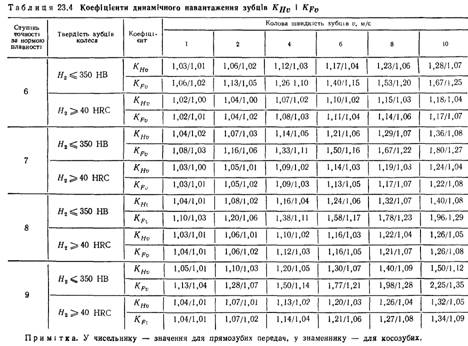
Динамічне навантаження у зачепленні зубчастих
передач. Неминучі похибки у виготовленні зубчастих коліс, а також
пружні деформації зубців під навантаженням спричинюють появу динамічних навантажень
зачеплення. Основний вплив на динамічні навантаження мають похибки основного
кроку Рb зубців
шестірні та колеса і їхня колова швидкість.
Якщо
основний крок зубців колеса більший від кроку зубців шестірні, то відбувається
передчасний вхід у зачеплення кромки зубця колеса – кромковий удар зубців. У
випадку, коли крок зубців менший від кроку зубців шестірні, має місце
запізнення виходу із зачеплення попередньої пари зубців – серединний удар
наступної пари зубців. Щоб зменшити ефект кромкового удару в зачепленні, треба
використовувати зубчасті колеса з модифікацією профілів головок зубців.
Вплив
динамічного навантаження на контакту міцність активних поверхонь зубців та
міцність зубців на згин оцінюється коефіцієнтами відповідно КHV та KFV.
Точне визначення цих коефіцієнтів достатньо складне і для розрахунків зубчастих передач можна
використати наближені значення коефіцієнтів КHV і KFV. При цьому колову швидкість
зубців визначають за формулою: v = 0.5·ω1·d1
Розрахунок
активних поверхонь зубців на контактну втому зводиться до визначення
розрахункових контактних напружень і порівняння цих напружень із допустимими.
Згідно з умовою контактної міцності:
![]()
розрахунок ведеться для моменту зачеплення
зубців у полюсі, оскільки втомне викришування активних поверхонь починається в
зоні полюсної лінії контакту на ніжках зубців.
У
зубчастій передачі питоме розрахункове навантаження qH на лінії контакту зубців визначається за
виразом (64). Після підстановки виразів для qH та 1/ρзв у записану вище
умову дістанемо:
![]()
Якщо
взяти cosαn·sinαn = 0,5sin2αn та позначити:
![]() ;
; ![]() ,
,
то дістанемо остаточну залежність для
розрахунку активних поверхонь зубців на контактну втому:
![]() . (68)
. (68)
Тут WHt – питома розрахункова
колова сила, що визначається за формулою (65):
WHt = (FHt/b) · КHα, · КHβ, KHv.
В
умові міцності (68) маємо: ZM
– коефіцієнт, що враховує механічні властивості матеріалів спряжених у
передачі коліс; для сталевих зубчастих коліс: ZM = 275 МПа1/2; для поєднання
сталь – чавун ZM = 215
МПа1/2; для чавунних коліс ZM = 200
МПа1/2; ZH – коефіцієнт форми спряжених
поверхонь зубців; для зубчастих передач із зміщенням (xΣ ≠ 0) ZH визначають за відповідними графіками, а для
передач без зміщення xΣ
= 0) – за записаною вище спрощеною залежністю при αn = 20° ZH
= 1,77cosβ; Zε–
коефіцієнт сумарної довжини контактних ліній; для прямозубих передач та
косозубих при εβ
≤ 0,9 Zε , Zε = ![]() , а для косозубих при εβ
> 0,9 та шевронних передач Zε =
, а для косозубих при εβ
> 0,9 та шевронних передач Zε = ![]() .
.
Розрахунок
активних поверхонь зубців на контактну втому за умовою (68) є основним для
зубчастих передач. У розрахунках
зубців на контактну втому допускається розрахункове контактне напруження у
межах
1,05[σ]H ≥ σH ≥ 0,9[σ]H.
Якщо ця умова не виконується, то можна змінити відповідно ширину вінця колеса b2, не виходячи за
межі рекомендованих значень ψbа. Якщо це не дає бажаного
результату, то змінюють міжосьову відстань або назначають інші матеріали коліс
чи іншу термообробку і розрахунок повторюють.
Розрахунок активних поверхонь зубців на контактну
міцність при дії максимального навантаження виконують з метою, щоб
запобігти появі залишкової деформації або крихкого руйнування поверхневого
шару зубців при короткочасних перевантаженнях передачі. Умова відсутності появи руйнувань зубців має
вигляд:
σн max
≤ [σ]н max, (69)
де σн max – максимальне
розрахункове контактне напруження, що виникає при найбільшому навантаженні Т1тах із спектра навантажень, які підводяться до передачі
навіть при однократній дії за період експлуатації; [σ]н max
– допустиме граничне контактне напруження.
Враховуючи,
що контактне напруження пропорційне квадратному кореню з навантаження, умову
(69) перепишемо так:
σн max
= σн
![]() . (70)
. (70)
де σн – розрахункове контактне
напруження, що виникає у зубцях при навантаженні Т1Н (визначають за виразом
(68)).
Розрахунок зубців на втому при згині. При
розрахунках на згин зубець розглядають як консольну балку. Розрахункове
навантаження прикладається до вершини зубця, тобто вибирають найнебезпечніший
випадок навантаження зубця з точки зору виникнення максимального напруження
згину у його основі.
На
рис. 26 зображена розрахункова схема зубця. Зубець завдовжки
Перенесемо
точку прикладання сили qF
на вісь симетрії зубця і розкладемо цю силу на дві взаємно
перпендикулярні складові:
qFt
= qF cos α’;
qFr = qF
sin α’, де α’ – кут, що визначає положення вектора
навантаження qF щодо
осі зубця.
У
небезпечному перерізі, який розміщений в основі зубця у зоні найбільшої
концентрації напружень, навантаження qFt
спричинює напруження згину σзг, а навантаження
qFr– напруження
стиску σст (див. епюри на рис. 26):
σзг = qFt ·
l/W0 = 6 · qF · l · cos α’/α2;
σст =
qFr /A = qF ·
sin α’/α.
На
рис. 26 показана також епюра сумарних напружень σf у небезпечному перерізі зубця.
Оскільки втомні тріщини і руйнування починаються на розтягнутому боці зубців
(тобто з боку робочого профілю), міцність зубців розраховують саме з цього боку
за умовою, що
σf = Yβ·
(σзг – σст) · αk ≤ [σ]F, (71)
де Yβ – коефіцієнт, що
враховує зменшення напружень при нахиленому розміщенні зубців у косозубих
передачах; αk –
теоретичний коефіцієнт концентрації напружень.
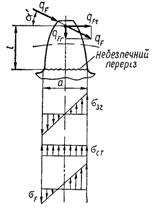
Рис. 26. До визначення напружень згину в
зубці зубчастого колеса
Розміри
l і a (див. рис. 26)
пропорційні модулю зубців тп
: l = λ1 · тп : а =
λ · 2тп (λ1
і λ2 – коефіцієнти пропорційності). Якщо це взяти до уваги та
підставити значення σзг та σст в умову (29), то
дістанемо:
σf = Yβ
· αk · [6qF ·
λ1 · mn · cos α’/( λ22
· m2n) – qF
· sin α’/( λ2
· mn )] =
= (qF ·Yβ · αk/mn ) (6 · λ1
· cos α’/ λ22
– sin α’/ λ2) ≤ [σ]F.
Врахуємо
залежність (65) для визначення розрахункового навантаження на зубці.
Остаточна
формула для розрахунку зубців на втому при згині набуде вигляду:
Σf
= YF · Yε · Yβ · WFt/mn <
[σ]
f .
(72)
Тут WFt – питома
розрахункова колова сила, яка визначається за формулою (21):
WFt= (FFt/b) · КFα, КFβ,
KFv.
В
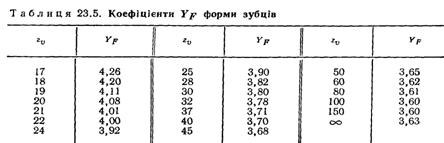
умові міцності (30) маємо такі коефіцієнти: YF – коефіцієнт форми зубців (залежить від
розмірів l, а, α’ та
форми перехідної кривої зубця, яка впливає на αk); YF визначають за
відповідними графіками залежно від еквівалентного числа зубців ZV
шестірні та колеса з урахуванням коефіцієнтів зміщення х; для некоригованих коліс (х = 0) зовнішнього зачеплення значення YF наведені
у табл. 5, а для коліс внутрішнього зачеплення наближено можна брати:
YF = 4z /(z + 20);
Yε –
коефіцієнт перекриття зубців, у розрахунках прямозубих та косозубих (шевронних)
передач можна наближено брати Yε
= 1; Yβ
– коефіцієнт нахилу зубців, для прямозубих передач Yβ = 1, а для косозубих та шевронних Yβ = 1– β/140°.
Перевірку
міцності зубців на втому при згині виконують для зубців шестірні і колеса,
оскільки YF1 та YF2 різні при z1
≠ z2.
Із
співвідношення (72) видно, що за інших рівних умов напруження згину в зубцях
тим більші, чим менший модуль зубців тп. Міцність зубців на
згин для передачі з відомою міжосьовою відстанню можна підвищити, збільшуючи
модуль та зменшуючи відповідно числа зубців шестірні та колеса.
Розрахунок
зубців на міцність при згині максимальним навантаженням виконують для того,
щоб запобігти появі залишкової деформації або крихкої поломки зубців. Цей
розрахунок ведуть за найбільшим короткочасним навантаженням T1 max для зубців того зубчастого колеса (шестірні
або колеса), для якого напруження згину σF більше.
Щоб
забезпечити потрібну міцність зубців, треба виконувати таку умову:
σн max
= σF ·
(T1 max / T1 F) ≤ [σ] F max,
(73)
де σF max – максимальне розрахункове напруження згину; σF – розрахункове напруження згину,
що спричинюється дією навантаження T1F; [σ] F max
– допустиме граничне напруження
згину.
Проектний
розрахунок. Добуті вище розрахункові залежності σН; σH max;
σF; та σF max
використовують для перевірних розрахунків на міцність зубчастих передач
із відомими розмірами та навантаженням.
Проектний
розрахунок має бути тільки для попереднього визначення орієнтовних розмірів
передачі і не може замінити виконання перевірних розрахунків, які є основними.
Габаритні
розміри зубчастої передачі визначаються умовою стійкості активних поверхонь
зубців проти втомного викришування. Тому розрахункову залежність для визначення
основного розмірного параметра передачі, який визначає її габаритні розміри,
дістанемо з умови (68). Таким розмірним параметром для циліндричних зубчастих
передач можна вважати міжосьову відстань aW.
Вихідними
даними для проектного розрахунку передачі є такі: розрахункове тривало діюче
навантаження T1H передаточне
число передачі u; параметр ψba
= b/aW або
ψbd = b/d1 рекомендації
для вибору яких наведені у 1; вид передачі – прямозуба чи косозуба (шевронна);
типовий режим навантаження передачі та строк її служби; матеріали зубчастих
коліс, їх термообробка, твердість активних поверхонь зубців; за цими даними
попередньо розраховують допустиме контактне напруження [σ]н.
Вивід
формули для визначення мінімально допустимої міжосьової відстані передачі aW
подамо у певній послідовності. У формулі (68) виконаємо заміну дістанемо:
σн = ZM · ZH · Zε · ![]()
Із
записаного співвідношення визначимо aw:
aW ≥ (u ± 1) · ![]() .
.
Якщо
додатково позначити:
Кa = ![]() ,
,
то можна дати остаточний запис формули для
визначення мінімальної міжосьової відстані передачі у такому вигляді:
aw min = Ка · (u ± 1) · ![]() . (74)
. (74)
У
формулі (74) обертовий момент ТІH
слід брати у ньютон-метрах (Нм), допустиме напруження [σ]н – у
мегапаскалях (МПа), а міжосьову відстань awmin
– у міліметрах (мм)
Допоміжний
коефіцієнт Ка у
формулі (74) враховує параметри передачі, які попередньо можуть бути вибрані
цілком однозначно, і параметри, які не можуть бути завчасно і точно визначені
(Zε, КHα, KHv). Тому коефіцієнту Ка
надається деяка наближена оцінка і рекомендується брати: Ка = 495 МПа1/3,
Ка = 415 МПа1/3 – для прямозубих передач із сталевими та
чавунними зубчастими колесами відповідно;
Ка =430 МПа1/3, Ка = 360 МПа1/3
– для косозубих (шевронних) передач із сталевими та чавунними колесами
відповідно.
Коефіцієнт
КНβ що враховує
нерівномірність розподілу навантаження по ширині зубчастих вінців, вибирають
залежно від параметра ψbd
за графіками на рис. 8.
Формула
(74) дає змогу оцінити ступінь впливу окремих параметрів передачі u, ψbd, [σ]н на її
габаритні розміри.
Обчислена
за формулою (74) міжосьова відстань awmin
дає можливість визначити модуль зубців та розміри вінців зубчастих коліс.
Потрібний модуль може бути визначений за формулою
m’n = 2aw min · cos β / (z1+z2). (75)
Значення
mn округляють
до найближчого стандартного значення mn
згідно з ГОСТ 9563–60.
Із
співвідношення (75) видно, що при одній і тій же міжосьовій відстані передачі
можна дістати різні модулі зубців при зміні чисел зубців шестірні Z1
та колеса z2. При великих значеннях z1 і відповідно
z2 = u∙z1
маємо зубчасті колеса із малим модулем, а при малих значеннях z1
та z2 – із великим модулем.
Маломодульні
колеса з великим числом зубців мають переваги за умовою підвищеної плавності
роботи (збільшується εα) та за економічними міркуваннями.
При малих значеннях т зменшуються втрати на тертя у зачепленні
(зменшується ковзання), скорочуються витрати матеріалу (зменшується da),
економиться час при нарізуванні зубців (зменшується кількість матеріалу, який
зрізається). Однак при малих модулях зростають вимоги до точності та жорсткості
передачі, суттєво зменшується міцність зубців на згин.
Великомодульні
колеса з великими розмірами зубців не так чутливі до спрацювання, можуть
працювати тривалий час після початку втомного викришування активних поверхонь,
менш чутливі до перевантажень та неоднорідності матеріалу, але плавність
роботи передачі з такими колесами значно падає.
Виходячи
з наведених міркувань, для силових зубчастих передач рекомендують брати m ≥
Здебільшого
число зубців шестірні z1 > zmin, де zmin –
мінімальне число зубців за умови непідрізання ніжок. Для некоригованих
прямозубих коліс zmin= 17, а для коліс із кутовою корекцією мінімальне
число зубців може бути 10. У косозубих та шевронних колесах мінімальне число
зубців залежить від кута нахилу лінії зубців, наприклад, якщо β = ..24°,
то zmin= 14, а якщо:
β
= 31°, то zmin = 12.
З
метою зменшення шуму у швидкохідних передачах рекомендують брати z1 ≥
Щоб
остаточно впевнитись у правильності вибору чисел зубців z1, z2
і модуля m, треба
перевірити міцність зубців на втому при згині. У разі отримання незадовільного
результату зменшують у допустимих межах z1 і відповідно z2
і тим самим збільшують модуль m.
Слід
зазначити, що при перевірці міцності зубців на втому при згині можна дістати
σF значно менше від [σ]F. Це не є суперечливим
або недопустимим результатом, оскільки габаритні розміри передачі за несучою
здатністю обмежуються контактною міцністю активних поверхонь зубців, а не
їхньою міцністю на згин.
Якщо
розрахункове напруження σF перевищує допустиме [σ]F, то, крім збільшення модуля
зубців, можна застосовувати зубчасті колеса із зміщенням. У таких випадках
вирішальне значення має не контактна міцність, а міцність зубців на згин. На
практиці такі випадки можуть бути у зубчастих колесах із твердістю активних поверхонь
зубців Н > 50...60 HRC у
реверсивних передач.
Особливості розрахунку відкритих зубчастих передач. У
відкритих передачах використовують прямозубі циліндричні або конічні колеса.
Такі передачі працюють при колових швидкостях зубчастих коліс не більш як
2 м/с. Зубці відкритих передач припрацьовуються при довільних твердостях
їхніх робочих поверхонь. Здебільшого колеса виготовляють із нормалізованих
або поліпшених сталей. У процесі роботи передачі зубці інтенсивно
спрацьовуються, що визначає особливості їхнього розрахунку.
Відкриті
передачі проектують з вузькими колесами (коефіцієнт ширини вінця ψba = 0,10...0,15). Розміри передачі
визначають із розрахунку на контактну втому з подальшою перевіркою на згин (за
аналогією закритих передач). Міжосьову відстань передачі визначають за
формулою (74), При цьому коефіцієнти, що враховують розподіл навантаження по
ширині вінця коліс, беруть КНβ
= КНF =1.
Спрацювання
зубців у відкритих передачах допускається до 25 % початкової їхньої товщини по
ділильному колу. Міцність зубців на згин при цьому зменшується приблизно у 2
рази. Тому треба так підібрати модуль зубців, щоб розрахункове напруження згину
σF за
формулою (72) було

