ЛАБОРАТОРНА
РОБОТА №8
Тема: Гармонійний аналіз часового
ряду.
Мета заняття:
ü На основі вихідних даних побудувати кореляційне поле часового
ряду та визначити вид залежності.
ü Знайти оцінки параметрів лінії регресії по даній стохастичній
залежності.
ü Оцінити адекватність моделі статистичним даним з ймовірністю
Р=0,95.
ü З ймовірністю Р=0,95 визначити наявність автокореляції в
залишках.
У випадку наявності в залишках невиявленої залежності,
визначити:
ü форму залежності;
ü невідомі коефіцієнти у моделі та їх значущість з ймовірністю
Р=0,95;
ü періодичну складову.
ü Включивши періодичну складову у модель тренда, визначити
наявність автокореляції у залишках для отриманої сумарної моделі.
ü З ймовірністю Р=0,95 визначити адекватність отриманої моделі
експериментальним даним.
Хід роботи
1.
Завантажити програму
EXCEL.
2. 
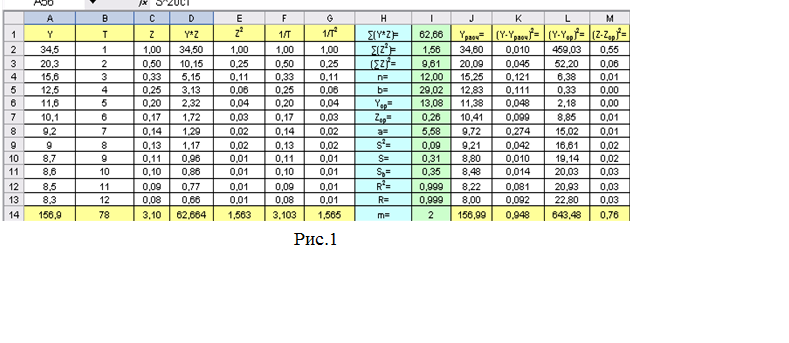
Сформувати таблицю
вихідних даних, заповнивши діапазон комірок А1:С13 (рис. 1).
3.
За допомогою майстра побудови діаграм побудувати кореляційне
поле даної статистичної вибірки (див. рис.2)
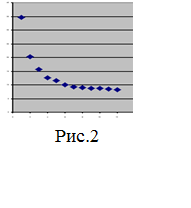
По виду
кореляційного поля (так як з ростом Т
- Y в
основному зменшується) припускається наявність гіперболічної залежності.
4. Як модель залежності може
бути прийнята гіперболічна крива функції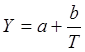 
.
5.
Приведемо модель до лінійного виду шляхом заміни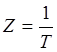 
. Тоді відповідно до МНК для лінійної залежності Y=a+bZ
оцінка параметрів рівняння визначаються
за формулами: 
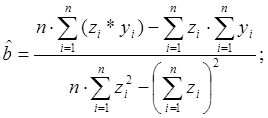
, де n - об’єм
вибірки.
6. Виконаємо допоміжні
розрахунки:
- значення y*z знайти у діапазоні D2: D13;
- значення z2 знайти у діапазоні Е2: Е13;
- значення 1/T знайти у діапазоні F2: F13;
- значення 1/T2 знайти у діапазоні G2: G13.
- значення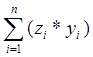 
знайти у комірці I1,
використовуючи вбудовану функцію СУММ або Автосумму;
- значення 
знайти у комірці С14;
- значення 
знайти у комірці А14);
- значення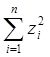 
знайти у комірці I2;
- значення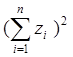 
- у комірці I3.
(Формули ввести самостійно).
7. Знайдемо значення оцінки
параметра b у комірці I5:
=(I4*D14-C14*A14)/(I4*I2-I3).
8. Для обчислення значення
оцінки параметра а знайдемо:
- середнє значення для Y
у комірці I6, використовуючи вбудовану функцію СРЗНАЧ;
- середнє значення для Z
у комірці I7.
9. Знайдемо значення оцінки
параметра а у комірці I8:=I6-I5*I7.
10.
У стовпці J обчислимо розрахункове значення для Yрозр. Для цього у комірку J2
введемо формулу J2:=$I8$+$I5$/B2, закріпивши при цьому абсолютні посилання за
комірками I8 й I5. Використовуючи операцію автозаполнення, скопіювати формулу у
діапазон J3: J13.
11.
Значення (y-yрозр)2,
, 
, 
розрахуємо у стовпцях K, L, M
відповідно (формули ввести самостійно).
12.
Обчислимо Sb за формулою: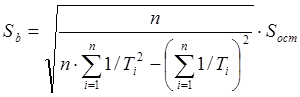 
, де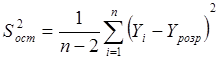 
Для цього:
- у комірці I9 обчислимо S2ост I9: =K14/(I4-2);
- у комірці I10 обчислимо S I10:= КОРІНЬ(I9);
- у комірці I11
обчислимо Sb I11:=КОРІНЬ(I4/((I4*G14)-(F14)^2))*I10
(рис.1).
Оцінимо параметр b на значущість відмінності від нуля за
критерієм Стьюдента.
13.
Обчислимо розрахункове значення критерію Стьюдента за
формулою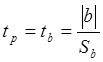 
у комірці В17:=I5/I11.
14.
У комірці В16 знайдемо табличне значення критерію Стьюдента,
використовуючи вбудовану функцію СТЬЮДРАСПОБР (ймовірність 0,05;
число ступенів вільності k=n=m-1=12-2=10).
15.
Зробимо висновки.
Адекватність моделі
перевіримо за критерієм Фішера.
Розрахункове значення критерію обчислимо за формулою: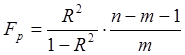
, де R – коефіцієнт кореляції, якій знаходиться за формулою:
.
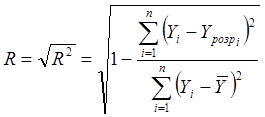16.
Обчислимо значення R2
у комірці I12:=1-(К14/L14), потім у комірці I13 знайдемо R - I13:=КОРІНЬ(I12).
17.
Знайдемо розрахункове значення критерію Фішера у комірці B18:
=(I12/(1-I12))*((I4-I14-1)/(I14)).
18.
Табличне значення
критерію Фішера обчислимо у комірці В19 за допомогою вбудованої функції FРАСПОБР
(ймовірність 0,05; число ступенів вільності k1=m=1 k2=n-m-1=12-2=10) (рис.1).
19.
Зробимо висновки про адекватність моделі.
Для перевірки правильності
моделі визначимо наявність автокореляції у залишках з використанням критерію
фон Неймана.
20.
Розрахункове значення критерію обчислимо за формулою:
, де Ut – значення залишків, тобто 
:
-
розрахуємо значення Ut у діапазоні С17:С28. Для цього у
комірку C17 введемо формулу C17:=A2-J2;
використовуючи операцію автозаполнення, скопіювати формулу у заданий діапазон;
-
розрахуємо значення Ut-Ut-1 у діапазоні D18:С28. Для цього у комірку D18 введемо формулу D18:=C18-C17; використовуючи
операцію автозаполнення, скопіювати формулу у заданий діапазон;
-
розрахуємо значення Ut2 у діапазоні Е17:Е28. Для цього у комірку Е17 введемои формулу E17:=(C17)^2; використовуючи
операцію автозаполнення, скопіювати формулу у заданий діапазон;
-
розрахуємо значення (Ut-Ut-1)2 у діапазоні DF18:F28. Для цього у комірку F18 введемо формулу F18:=(D18)^2; використовуючи
операцію автозаполнення, скопіювати формулу у заданий діапазон;
-
знайдемо суми цих стовбців у комірках С29, D29, Е29 та F29 відповідно.
21.
Обчислимо у комірці I17 розрахункове значення
критерію фон Неймана I17:=(I4*F29)/((I4-1)*E29) (рис.3).
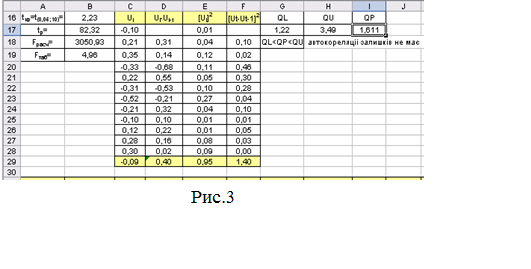
22.
У комірках G17 та H17 знайдємо QL й QU
– табличні критичні значення для критерію фон Неймана, (QL=1,22,
QU=3,49).
23.
Зробимо висновки про наявність автокореляції злишків.
24. 
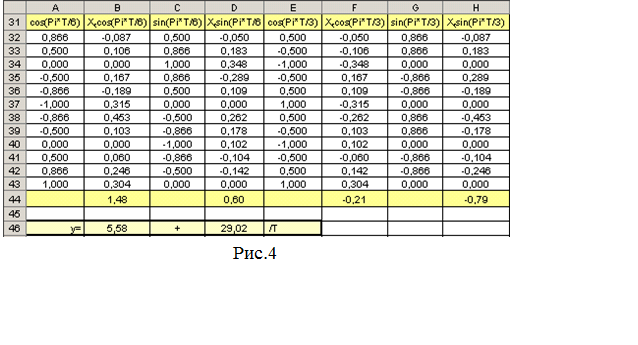У діапазоні А46:Е46 запишемо остаточну модель 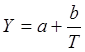(рис.4)
Подальші розрахунки зробимо з метою обчислення
коефіцієнтів гармонійних коливань.
25. Виділимо періодичну складову. Для цього при Т=12
розрахуємо коефіцієнти:
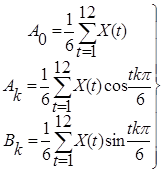
26.
Знайдемо проміжні величини, використовуючи вбудовані функції COS,
SIN, ПИ:
- 
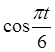(А32:=COS(ПІ()*В2/6)),
- 
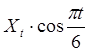(В32:=С17*А32),
- 
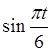(С32:
=SIN(ПІ()*В2/6)),
- 
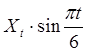(D32:=C17*C32),
- 
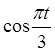(E32:=COS(ПІ()*В2/3)),
- 
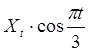(F32:=C17*E32),
- 
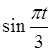(G32:=SIN(ПІ()*В2/3)),
- 
(H32: =C17*G32)
(рис.4).
27.
Беремо дві гармонії К=1,2 та обчислимо коефіцієнти
гармонійних коливань у відповідних комірках: A50:=0, B50:=B44/6, C50:=D44/6,
D50:=F44/6, E50:=H44/6.
28.
Розрахуємо квадрати амплітуд коливань за
формулою: 
. Значення R12
розмістимо у комірці F50:=(B50)^2+(C50)^2; значення R22 - у комірці G50:=(D50)^2+(E50)^2.
Перевіримо ці амплітуди на значимість від нуля. Для цього:
29. 
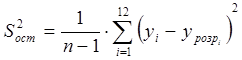Обчислимо
у комірці H50:=K44/11.
Знайдемо для кожного Rк статистику Фішера за формулами: 
(J49:=2*H50/F50),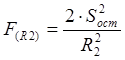 
(J50:=2*H50/G50),
табличне значення критерію Фішера Fкр
обчислимо у комірці J51 за допомогою вбудованої функції FРАСПОБР (ймовірність
0,05; число ступенів вільності k1=m=1 k2=n-m-1=12-2=10) (рис.5).
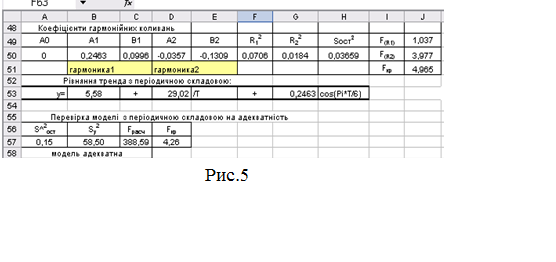
30.
Зробити висновки.
31.
Розрахуємо P1(t) у комірці I32
=$B$50*A32+$C$50*C32 (при введенні формули використовуємо абсолютне посилання
на комірки В50 і С50). Використовуючи операцію автозаполнення, скопіювати
формулу у діапазон I33:I43.
32.
Розрахуємо 
у комірці J32:=J2+I32.
Використовуючи операцію автозаполнення, скопіювати формулу у діапазон J33:J43.
33.
Розрахуємо (
)2 у комірці К32:=(А2-J32)^2. Використовуючи
операцію автозаполнення, скопіювати формулу у діапазон К33:К43.
34.
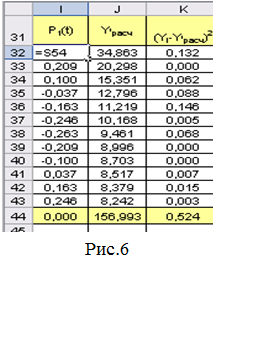Знайдемо суми цих стовбців у комірках I44, J44; та К44 відповідно
(рис.6).
35.
Запишемо рівняння тренда з періодичної складовою у діапазоні
А53:К53 (рис.5).
Перевіримо модель з періодичної складовою на адекватність. Для
цього:
36. Знайдемо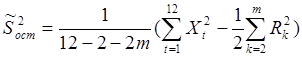 
у комірці
А57:=(E29-0,5*(F50+G50))/6.
37.
Розрахуємо Sy2
у комірці В57, використовуючи вбудовану функцію ДИСП (діапазон А2:А13).
38.
Обчислимо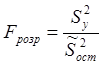
у комірці
С57:=В57/А57.
39.
Табличне значення знайдемо за допомогою
вбудованої функції FРАСПОБР у комірці D57
(рис.5).
40.
Підвести підсумки лабораторної роботи і зробити висновки.
41.
Зберегти книгу у своїй робочій папці під ім'ям Лаб.8.
Висновки:
1.
Оскільки Fроз>Fтаб, то з надійністю Р=0,95
математичну модель 
можна вважати
адекватною експериментальним даним.
2.
При перевірці по критерію фон Неймана автокореляції залишків
не виявлено.
3.
Виділено періодичну складову та за допомогою критерію Фішера
перевірено на значущість амплітуди гармонійних коливань.
4.
Оскільки Fроз>Fтаб, то з надійністю Р=0,95
математичну модель з неперіодичною і періодичною складовою 
можна вважати
адекватною.
Завдання до лабораторної роботи №8
|
T |
1 |
2 |
3 |
4 |
5 |
6 |
|
Yt |
25,5+а |
17,5+а |
13+а |
8,5+а |
6,3+а |
6,1+а |
|
T |
7 |
8 |
9 |
10 |
11 |
12 |
|
Yt |
5,6+а |
3,1+а |
1,2+а |
1,3+а |
4,4+а |
9+а |
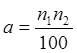, де n1n2 –
двозначне число, n1 –
передостання цифра, а n2
- остання цифра залікової книжки.
