ЛЕКЦІЯ 4. «Лінійні моделі множинної регресії»

Анотація

Множинна регресія. Специфікація багатофакторної моделі. Мультиколінеарність. Помилки специфікації множинної регресії. Практичні наслідки мультиколінеарності. Ознаки мультиколінеарності та методи її усунення. Оцінка якості моделі множинної регресії. Перевірка виконання передумов МНК. Етапи побудови економетричної моделі.

4.1 Загальна лінійна множинна модель

На будь-який економічний показник Y, як правило, впливає не один, а декілька факторів (регресорів) . Так, наприклад, попит населення на певний товар буде визначатися не тільки ціною на нього, але й цінами на його замінники, доходами споживачів й іншими факторами. У низці досліджень аналізується зв’язок доходу працівника певної галузі виробництва з його рівнем освіти, віком, стажем роботи в цій галузі.

В подібних випадках маємо справу з множинною лінійною моделлю (регресією), що описує взаємний зв’язок між залежною змінною Y та регресорами і яку можна подати такому вигляді:

(4.1)

Цей математичний запис інформує про функціональну залежність умовного математичного сподівання залежної змінної Y від m регресорів (незалежних, пояснюючих) змінних Х.

Отже, постає задача виявлення статистичного взаємозв’язку між Y та Х.

Загальний запис теоретичної лінійної множинної регресії може бути зроблений в такому вигляді:

, (4.2)

де – теоретичні коефіцієнти регресії (часткові коефіцієнти) або параметри теоретичної регресії, які характеризують реакцію залежної змінної на зміну кожного регресора ;

– вільний член, який визначає значення за умови, коли значення регресорів дорівнюють нулеві;

– значення -го регресора при і-ому спостереженні;

– випадковий збудник при і-ому спостереженні.

Для однозначного визначення параметрів моделі (4.2) необхідно, щоб виконувалась нерівність

де n – число спостережень;

m – число регресорів в моделі.

У векторно-матричній формі теоретичну модель (4.2) можна подати так:

(4.3)

де

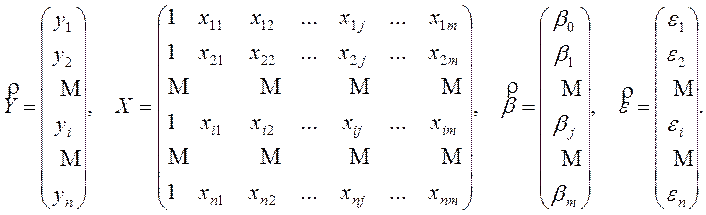
Компоненти вектора є величинами сталими (), але невідомими. Їх необхідно оцінити шляхом обробки вибірки, а тому надалі будемо мати справу із емпіричною моделлю, яка є прообразом теоретичної (4.2), (4.3):

(4.4)

Компоненти вектора є статистичними оцінками компонент теоретичного вектора лінійної множинної регресії (4.3), а компоненти вектора похибок – статистичні оцінки випадкових збудників вектора .

Якщо теоретичний вектор є величиною сталою і нам невідомою, то емпіричний вектор ми можемо визначити шляхом обробки статистичної інформації вибірки обсягом n. Враховуючи те, що вибірка складає лише незначну частину генеральної сукупності (n≤N), то інформація, яку одержимо при статистичній обробці, про регресори X_j моделі буде не повною і для кожної іншої вибірки буде потерпати певні зміни. Отже, компоненти емпіричного вектора будуть містити елемент випадковості. Таким чином, , як і сам вектор будуть випадковими величинами, які мають певні закони розподілу ймовірностей із відповідними числовими характеристиками.

Із вище наведеного можемо тепер стверджувати, що є статистичною оцінкою для теоретичного вектора . А тому постають питання математичної статистики: зміщена чи незміщена ця статистична оцінка; в якому довірчому інтервалі із заданою надійністю γ можуть перебувати теоретичні компоненти (параметри) і сама функція регресії; як здійснити перевірку на статистичну значущість теоретичних параметрів по заданому рівню значущості α.

Для вирішення цих питань нам необхідно визначити числові характеристики для параметрів (j=0,1,2,...,m) і для самої функції регресії, використовуючи при цьому елементи матричної алгебри як інструментарію, застосовуючи який ми можемо без громіздких викладок отримати необхідні результати.

Оцінка параметрів моделі множинної регресії проводиться за допомогою методу найменших квадратів. Формула для розрахунків параметрів регресійного рівняння наступна:

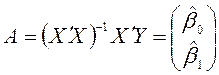. (4.5)

4.2 Специфікація моделі. Проблема мультиколінеарності

Маючи на увазі, що вибір аналітичної форми економетричної моделі не може розглядатись без конкретного переліку незалежних змінних, специфікація моделі передбачає добір чинників для економетричного дослідження.

При побудові моделі множинної регресії відбір найбільш істотних факторів, що впливають на результативну ознаку, проводиться на основі якісного, теоретичного аналізу у поєднанні з використанням статистичних прийомів. При цьому в процесі такого дослідження можна кілька разів повертатись до етапу специфікації моделі, уточнюючи перелік незалежних змінних та вид функції, що застосовується. Адже коли вид функції та її складові не відповідають реальним залежностям, то йдеться про помилки специфікації.

Помилки специфікації моделі можуть бути трьох видів:

1) ігнорування істотної пояснюючої змінної при побудові економетричної моделі;

2) введення до моделі незалежної змінної, яка не стосується вимірюваного зв’язку;

3) використання не відповідних математичних форм залежності.

При цьому порівняльний аналіз та відбір факторів до регресії може здійснюватися на основі кореляційного аналізу.

Одна з передумов застосування методу найменших квадратів до оцінювання параметрів лінійних багатофакторних моделей – відсутність лінійних зв’язків між незалежними змінними моделі. Якщо такі зв’язки існують, то це явище називають мультиколінеарністю.

Суть мультиколінеарності полягає в тому, що в багатофакторній регресійній моделі дві або більше незалежних змінних пов’язані між собою лінійною залежністю або, іншими словами, мають високий ступінь кореляції:

(4.6)

Наявність мультиколінеарності створює певні проблеми при розробці моделей. Насамперед, визначник матриці спостережень наближається до нуля, і оператор оцінювання за звичайним МНК стає надзвичайно чутливий до похибок вимірювань і похибок обчислень. При цьому МНК-оцінки можуть мати значне зміщення відносно дійсних оцінок узагальненої моделі, а в деяких випадках можуть стати взагалі беззмістовними.

Передусім потрібно зрозуміти природу мультиколінеарності.

Наприклад, коли вивчається залежність між ціною акції, дивідендами на акцію та отриманим прибутком на акцію, то дивіденди та отриманий прибуток на одну акцію мають високий ступінь кореляції. Іншими словами, виникає ситуація, коли два колінеарних фактори змінюються в одному напрямку У такому разі майже неможливо оцінити вплив кожного з них на досліджуваний показник.

З’ясуємо, до яких наслідків може призвести мультиколінеарність. Це одне з найважливіших питань, яке потрібно зрозуміти при розробці економетричних моделей.

Практичні наслідки мультиколінеарності:

- мультиколінеарність незалежних змінних (факторів) призводить до зміщення оцінок параметрів моделі, які розраховуються за МНК. На основі цих оцінок неможливо зробити конкретні висновки про результати взаємозв’язку між показником і факторами;

- збільшення дисперсії та коваріації оцінок параметрів, обчислених за методом найменших квадратів;

- збільшення довірчого інтервалу (оскільки збільшується середній квадрат відхилення параметрів);

- незначущість t-статистик.

Мультиколінеарність не є проблемою, якщо єдиною метою регресійного аналізу є прогноз (оскільки чим більше значення R², тим точніший прогноз). Якщо метою аналізу є не прогноз, а дійсне значення параметрів, то мультиколінеарність перетворюється на проблему, оскільки її наявність призводить до значних стандартних похибок оцінок параметрів.

Єдиного способу визначення мультиколінеарності, на жаль, немає. Зовнішні ознаки наявності мультиколінеарності такі:

- велике значення R² і незначущість t-статистики.

Наявність цих двох факторів одночасно є «класичною» ознакою мультиколінеарності. З одного боку незначущість t-статистики Стьюдента означає, що один або більше оцінених параметрів статистично незначуще відрізняються від нуля. З іншого боку, якщо значення R² велике, ми приймаємо з великою ймовірністю F-критерій Фішера, який відкидає нульову гіпотезу (Н₀: a₁=a₂ = ... = a_m =0). Суперечність свідчить про наявність мультиколінеарності;

- велике значення парних коефіцієнтів кореляції.

Якщо значення хоча б одного коефіцієнта кореляції між пояснюючими факторами є значущим, то мультиколінеарність є серйозною проблемою.

Зауважимо, що велике значення парних коефіцієнтів кореляції – достатня, але не необхідна умова наявності мультиколінеарності. Мультиколінеарність може мати місце навіть при відносно невеликих значеннях парних коефіцієнтах кореляції у більш ніж двофакторній регресійній моделі. З цією метою оцінюють частинні коефіцієнти кореляції.

Для визначення мультиколінеарності здебільшого застосовують такі тести:

- F-тecт, запропонований Глобером і Фарраром (ЛР.01);

- характеристичні значення та умовний індекс.

Перший із них базується на тому що за наявності мультиколінеарності один чи більше факторів пов’язані між собою лінійною або приблизно лінійною залежністю. Одним із способів визначення щільності регресійного зв’язку є побудова регресійної залежності кожного фактора х_i з усіма іншими факторами. Тому F-тест має іншу назву: побудова допоміжної регресії. Обчислення відповідного коефіцієнта детермінації для цього допоміжного регресійного рівняння та його перевірка за допомогою F-критерію дають змогу виявити лінійні зв’язки між незалежними змінними.

Тест, що застосовує характеристичні значення (власні числа матриці спостережень) та умовний індекс R (що обчислюється як відношення максимального власного числа матриці до її мінімального власного числа), використовується в сучасних статистичних пакетах. Ми не розглядатимемо його детально, бо це потребує застосування апарату теорії матриць.

Зазначимо лише, що за цим тестом розраховується не тільки умовне число R, а й умовний індекс . Якщо 100 ≤ R ≤ 1000, мультиколінеарність помірна, якщо R > 1000 – висока. Аналогічно, якщо 10 ≤ CI ≤ 33, мультиколінеарність помірна, якщо CI > 33 — висока.

Ми розглянули лише основні методи тестування мультиколінеарності. Жоден з них не є універсальним. Усі вони мають один спільний недолік: жоден із них не проводить чіткої межі між тим, що треба вважати “суттєвою” мультиколінеарністю, яку необхідно враховувати, і тим, коли нею можна знехтувати.

Виявлення мультиколінеарності є лише частиною справи. Інша частина – як її усунути. Безпомилкових і абсолютно правильних порад немає, оскільки мультиколінеарність є прикладною проблемою.

Звичайно, усе залежить від ступеня мультиколінеарності, однак у будь-якому разі можна запропонувати кілька простих методів усунення мультиколінеарності:

1) використання додаткової або первинної інформації;

2) об’єднання інформації;

3) відкидання змінної з високою кореляцією;

4) перетворення даних (використання перших різниць);

5) збільшення кількості спостережень.

Які поради спрацюють на практиці, залежить від істотності проблеми та її характеру. Якщо переліченими методами не вдається усунути мультиколінеарність, то для оцінювання параметрів багатовимірної моделі доцільно застосувати метод головних компонентів.

4.3 Оцінка якості моделі множинної регресії

Якість моделі регресії перевіряється на основі аналізу залишків регресії . Аналіз залишків дозволяє отримати уявлення про те, наскільки добре підібрана модель і наскільки правильно вибраний метод оцінки коефіцієнтів. Згідно загальним припущенням регресійного аналізу, залишки повинні вести себе як незалежні однаково розподілені випадкові величини. Дослідження доцільно починати з вивчення графіку залишків. Він може показати наявність якої-небудь залежності, що не врахована в моделі. Графік добре показує і викиди, яких потрібно позбавлятися.

Якість моделі оцінюється за наступними напрямками (аналогічно до парної регресії):

- перевірка якості рівняння регресії (індекс кореляції та коефіцієнт детермінації);

- перевірка значимості рівняння регресії (критерій Фішера);

- аналіз статистичної значущості параметрів моделі (t-критерій);

- перевірка виконання передумов МНК.

Умови, що необхідні для отримання незміщених, спроможних та ефективних оцінок, представляють собою передумови МНК. Виконання умови рівності нулеві математичного очікування залишків забезпечується завжди при використанні МНК для лінійних моделей. Передумова про нормальний розподіл залишків дозволяє проводити перевірку параметрів регресії за допомогою критеріїв t та F. разом з тим оцінки регресії, отримані методом МНК, мають добрі властивості навіть при відсутності нормального розподілу залишків. Таким чином, найважливішими є виконання умови незалежності та умови гомоскедастичності.

4.4 Етапи побудови економетричної моделі

Розглянемо етапи побудови та аналізу економетричних моделей на прикладі:

Приклад 1. Необхідно провести дослідження залежності ціни автомобіля (Y) від таких характеристик як вік авто (X₁) та його об’єм двигуна (X₂) на основі вибіркових даних, наведених в таблиці 4.1.

Таблиця 4.1

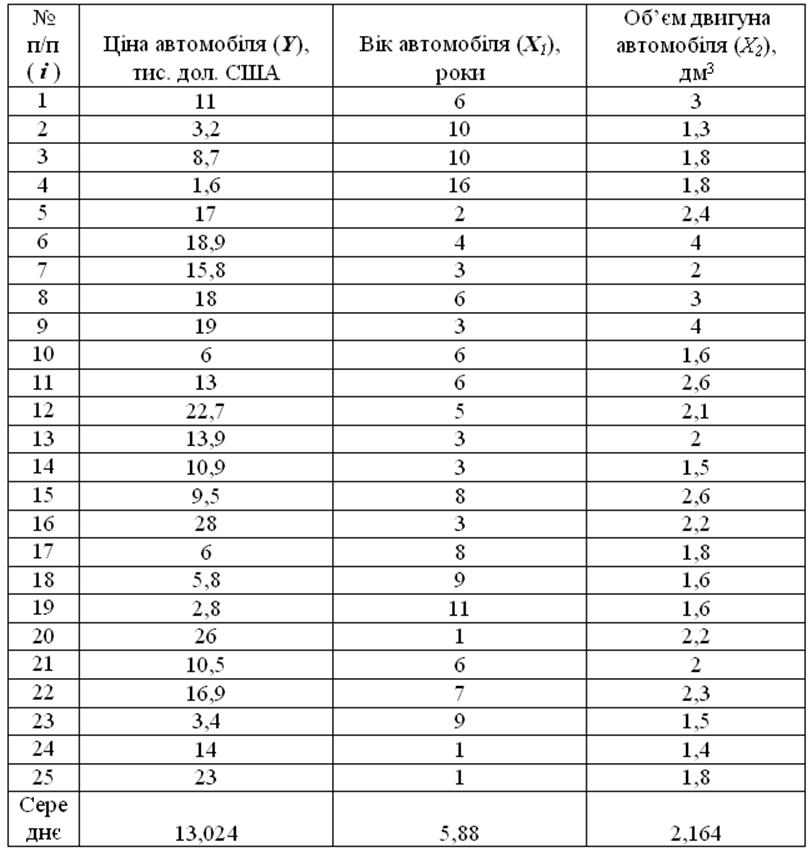
Припустимо, що між ціною та означеними технічними характеристиками існує лінійна залежність:

Необхідно:

1) обчислити статистичну оцінку вектора , тобто визначити для залежності між досліджуваним фактором Y (ціною автомобіля) та пояснюючими змінними X₁ (вік автомобіля) і X₂ (об’єм двигуна);

2) проаналізувати ступінь адекватності побудованої моделі та вибіркових даних;

3) виконати дисперсійний аналіз моделі та обчислити коефіцієнт множинної детермінації ;

4) перевірити статистичну значущість коефіцієнта детермінації на основі критерію Фішера;

5) визначити виправлені дисперсії та виправлені середньоквадратичні відхилення для статистичних оцінок ;

6) із заданою надійністю побудувати довірчі інтервали для параметрів ;

7) одержати прогнозне значення та побудувати для нього із заданою надійністю довірчі інтервали;

8) визначити часткові коефіцієнти еластичності .

1. Оцінка параметрів лінійної економетричної моделі

Оцінки параметрів визначимо за методом найменших квадратів. Запишемо теоретичну модель у векторно-матричному вигляді:

Сформуємо матрицю Х, першим стовпчиком якої будуть елементи, значення яких дорівнюють одиниці, іншими – значення пояснюючих змінних, та вектор , елементи якого складаються із значень залежної змінної.

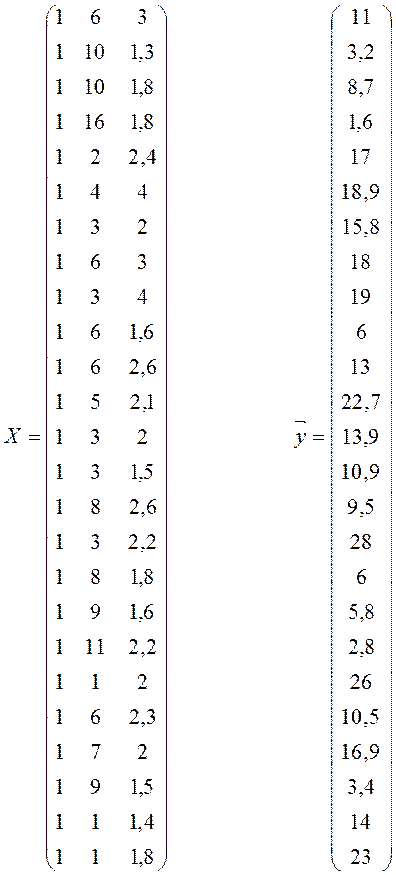
Транспонуємо матрицю Х:

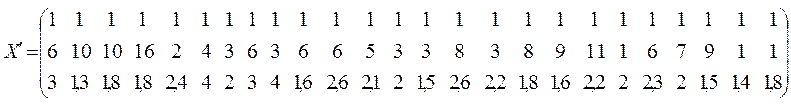
Перемножимо матрицю X^¢ спочатку на матрицю X, потім на вектор :

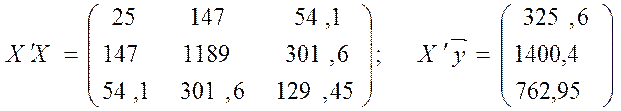Обчислимо матрицю, обернену до X^¢Х. Ця матриця існує, якщо визначник матриці X^¢Х не дорівнює нулю: . Тому спочатку розрахуємо визначник матриці X^¢Х:

det(X^¢Х)=93643,75.

Тоді:

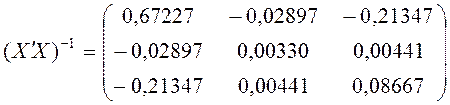Використовуючи формулу

знаходимо статистичні оцінки параметрів моделі за методом найменших квадратів:

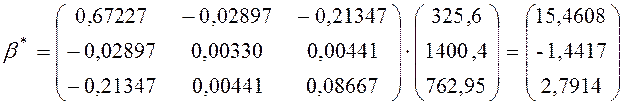Таким чином, .

Отже, залежність ціни автомобіля від його віку та об’єму двигуна має вигляд:

2. Аналіз ступеня адекватності побудованої моделі та вибіркових даних

Обчислимо вектор за формулою:

результати розрахунків наведено в табл. 4.2.

Таблиця 4.2

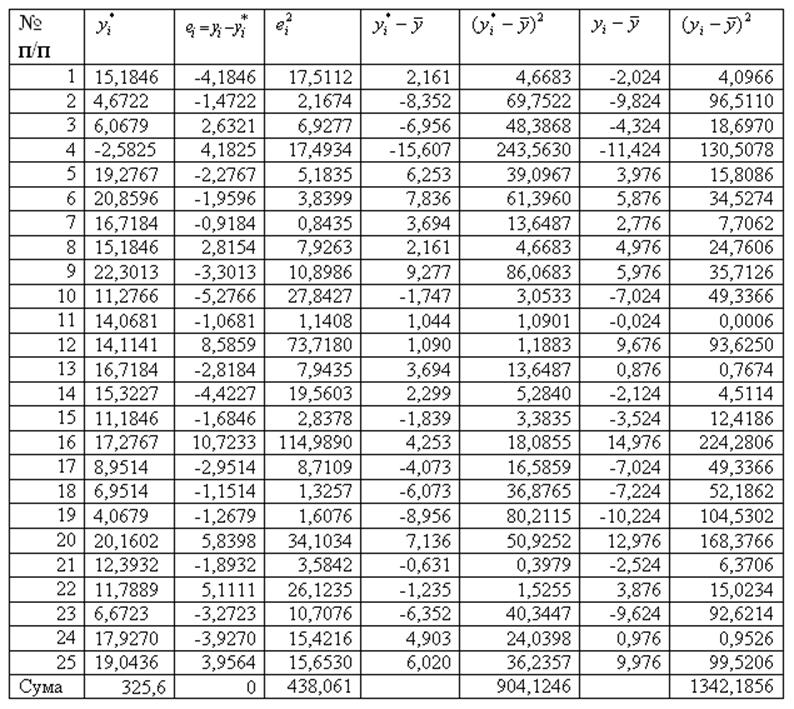
Правильність виконаних розрахунків можна перевірити, порівнюючи середні значення та , де:

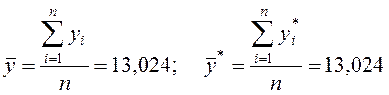оскільки , то попередні розрахунки є вірними.

Для подальшого статистичного дослідження моделі використаємо результати таблиці 4.2.

Визначимо ступінь адекватності моделі та статистичних даних через відхилення між фактичними значеннями та значеннями, обчисленими за моделлю. Запишемо їх як елементи вектора :

Середнє значення , отже розбіжностей не існує, модель адекватна.

3. Дисперсійний аналіз моделі та обчислення коефіцієнта множинної детермінації

Проведемо дисперсійний аналіз побудованої моделі. Відомо, що

Можна довести, що й для дисперсій цих змінних виконується рівність:

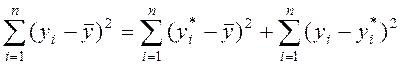Розрахунки табл. 4.2 підтверджують цей висновок. Користуючись розрахунками, наведеними в табл. 4.2, обчислимо коефіцієнт множинної детермінації:

;

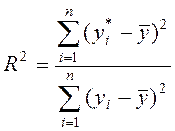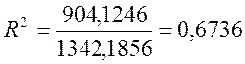3. Перевірка статистичної значущості коефіцієнта множинної детермінації за критерієм Фішера

Для перевірки статистичної значущості впливу регресорів на залежну змінну моделі використовуємо статистичний критерій Фішера:

;

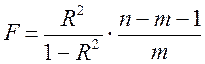при рівні значущості a=0,05 та ступенях свободи k₁=m=2 i k₂=n-m-1=22 по таблиці розподілу Фішера знаходимо =3,44.

Обчислимо спостережене значення критерію за формулою:

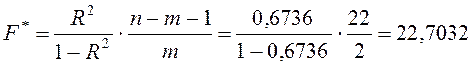Критерій Фішера має правобічну критичну область із критичною точкою робимо статистичний висновок:

оскільки >, то статистична гіпотеза відхиляється, отже всі регресори мають вплив на залежну змінну.

4. Визначення дисперсій оцінок параметрів та їх стандартних помилок

Знайдемо тепер незміщену оцінку для дисперсії залишків :

;

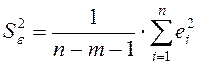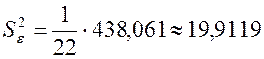Коваріаційна матриця оцінок параметрів дорівнює:

;

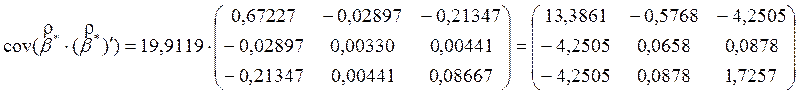
отже, дисперсії оцінок параметрів можна записати як:

Середньоквадратичні відхилення оцінок параметрів дорівнюють:

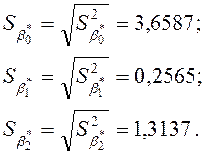
Перевіримо статистичну значущість параметрів , та . Для цього сформулюємо нульову гіпотезу Н₀: при альтернативній гіпотезі Н₁: :

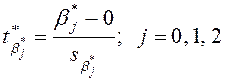
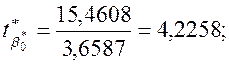
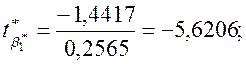
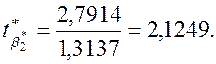
Аналогічно перевірці на статистичну значущість r_xy, знаходимо, що () і відхиляємо нульову гіпотезу Н₀ про рівність нулю параметрів , та .

5. Розрахунок довірчих інтервалів для оцінок параметрів , та із заданою надійністю

Довірчі інтервали для коефіцієнтів регресії визначаються за формулою:

де – задана надійність; – табличне значення.

Отже,

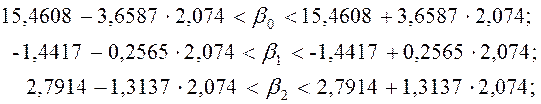
або

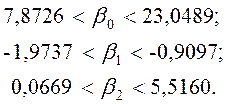
На основі побудованої залежності можна зробити висновок, що ціна автомобіля, який міг би мати технічні характеристики, рівні середнім значенням та , дорівнювала б завдяки середньому значенню залежної змінної – =13,024 тис.дол. Збільшення віку автомобіля на один рік зменшує ціну на 1,4417 тис.дол., а збільшення об’єму двигуна на 1дм³ призводить до збільшення ціни на 2,7914 тис.дол. Фактори, включені в модель, пояснюють “поведінку” ціни на 67,4%. Звичайно, це можна пояснити тим, що на формування ціни на автомобіль мають вплив також інші фактори (престиж марки, тип двигуна, оснащення салону, колір тощо), які в даному прикладі не розглядались.

6. Розрахунок прогнозного значення та побудова для нього із заданим рівнем значущості довірчих інтервалів

Значення ціни автомобіля суттєво залежить від його віку та об’єму двигуна, тому доцільно розрахувати точковий прогноз та довірчі інтервали прогнозу. Для цього задамо вектор прогнозних значень незалежних змінних . Розрахуємо точкове прогнозне значення:

Довірчі інтервали прогнозу визначаються як:

де – стандартна похибка прогнозу

Визначимо за формулою стандартну похибку прогнозного значення :

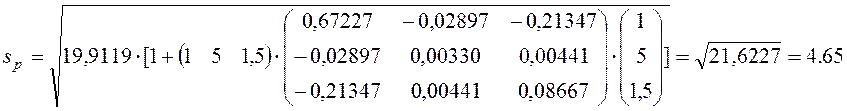та обчислимо нижню і верхню межу прогнозного значення :

або

Таким чином, ціна на автомобіль може коливатися приблизно від 2,8 до 22,0 тис.дол. Це пояснюється тим, що різні марки легкових автомашин відрізняються не тільки об’ємом двигуна, а й іншими технічними характеристиками.

7. Визначення часткових коефіцієнтів еластичності

Одержимо:

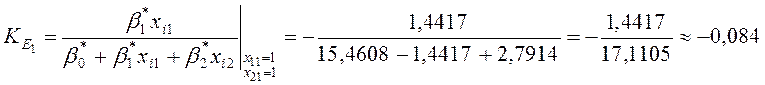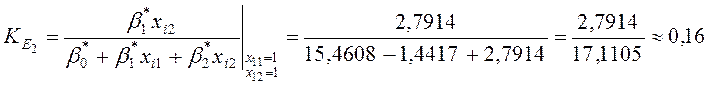Отже, інформує про те, що при збільшенні першого регресора (вік автомобіля) на k відсотків, значення залежної змінної моделі Y (ціна автомобіля) зменшиться на відсотків, а при збільшенні другого регресора (об’єм двигуна автомобіля) на k відсотків, Y збільшиться на відсотків.