ПРАКТИЧНА РОБОТА №2

 

Тема: ПОБУДОВА ТА АНАЛІЗ МОДЕЛІ ПАРНОЇ ЛІНІЙНОЇ РЕГРЕСІЇ

 

Мета роботи: побудувати та проаналізувати модель парної лінійної регресії.

Зміст роботи: проведення параметризації лінійного рівняння залежності двох факторів та оцінка статистичної значимості побудованої регресії і її параметрів. Здійснення прогнозу на основі побудованої моделі та оцінка його точності.

Вимоги до звіту: назва, тема, мета, завдання, розрахункові формули. Результати аналітичного розв’язання задачі та комп’ютерного у вигляді таблиці MS Excel з вихідними умовами експерименту, таблиці MS Excel з результатами обчислень, висновок про отримані результати. Опис інструментів та функцій MS Excel, що використовувались при вирішенні задачі. Короткий опис технології вирішення задачі в MS Excel.

 

ТЕОРЕТИЧНІ ВІДОМОСТІ

Приклад. По територіям регіону наводяться дані за 200X р.

 

Таблиця 1

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	78	133
2	82	148
3	87	134
4	79	154
5	89	162
6	106	195
7	67	139
8	88	158
9	73	152
10	87	162
11	76	159
12	115	173

 

Розв’язання

Для розрахунку параметрів рівняння лінійної регресії побудуємо розрахункову таблицю 2.

 

Таблиця 2

 

;

.

 

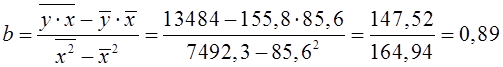Отримано рівняння регресії:

          .

Зі збільшенням середньодушового прожиткового мінімуму на 1 грн середньодобова заробітна плата зростає в середньому на 0,89 грн.

1.              Тісноту лінійного зв’язку оцінить коефіцієнт кореляції:

;      .

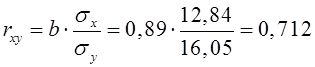Це означає, що 51% варіації заробітної платні () пояснюється варіацією фактору  – середньодушового прожиткового мінімуму.

Якість моделі визначає середня похибка апроксимації:

.

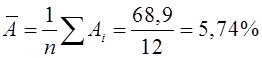Якість побудованої моделі оцінюється як добре, так як  не перевищує 8-10%.

3.              Оцінку значимості рівняння регресії в цілому проведемо за допомогою -критерію Фішера. Фактичне значення -критерію:

          .

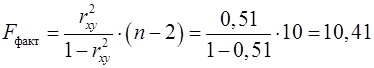Табличне значення критерію при пятивідсотковому рівні значимості та степенях свободи  і  складає . Так як , то рівняння регресії признається статистично значимим.

Оцінку статистичної значущості параметрів регресії проведемо за допомогою -статистики Стьюдента і шляхом розрахунку довірчого інтервалу кожного з показників.

Табличне значення -критерію для числа ступенів свободи  і  складає .

Визначимо вибіркові похибки , , :

;

;

.

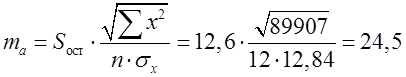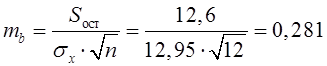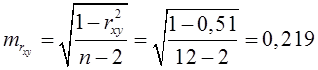Тоді

;

;

.

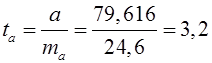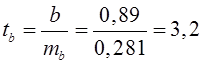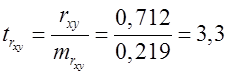Фактичні значення -статистики перевищують табличні значення:

;      ;     ,

тому параметри ,  і  не випадково відрізняються від нуля, а є статистично значимими.

Розрахуємо довірчі інтервали для параметрів регресії  і . Для цього визначимо граничну похибку для кожного показника:

;

.

Довірчі інтервали

Аналіз верхньої та нижньої границь довірчих інтервалів призводить до висновку про те, що з вірогідністю  параметри  і , знаходячись в зазначених межах, не приймають нульових значень, тобто не є статистично значимими і істотно відрізняються від нуля.

4.              Отримані оцінки рівняння регресії дозволяють використовувати його для прогнозу. Його прогнозні значення прожиткового мінімуму складе:  грн., тоді прогнозне значення заробітної платні складе:  грн.

5.              Помилка прогнозу складе:

 

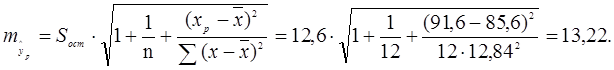
Гранична помилка прогнозу, яка в 95% випадків не буде перевищена, складе:

Довірчий інтервал прогнозу:

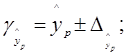
 грн.;

 грн.;

 

Виконаний прогноз середньодобової заробітної платні є надійним () і знаходиться в межах від 131,66 грн. до 190,62 грн.

6.              В завершенні розв’язання задачі побудуємо на одному графіку вихідні дані та теоретичну пряму (рис.1):

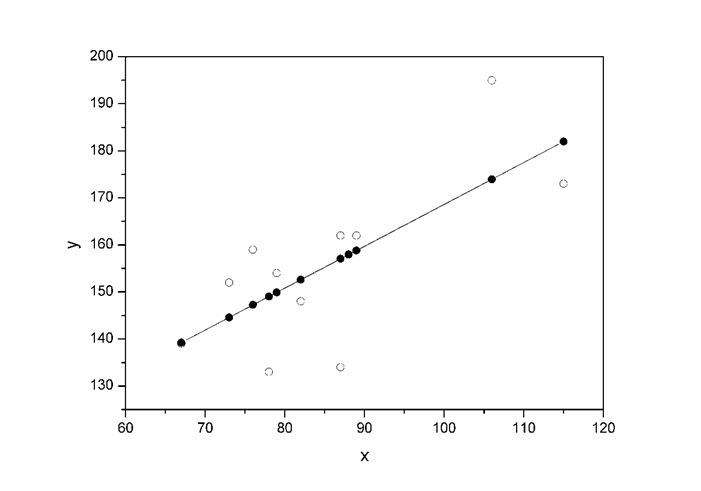
Рисунок 1

 

ПРАКТИЧНІ ЗАВДАННЯ

Побудувати лінійне рівняння парної регресії  від .

–        Розрахувати лінійний коефіцієнт парної кореляції та середню похибку апроксимації. Зробити висновок про зв'язок між  та  ( прямий чи обернений, тісний чи ні).

–        Оцінити статистичну значимість регресії та її параметрів за допомогою -критерію Фішера і -критерію Стьюдента при рівні значимості  p=0,95.

–        Виконати прогноз заробітної платні  при прогнозному значенні середньодушового прожиткового мінімуму , що складає 107% від середнього рівня.

–        Оцінити точність прогнозу, розрахувавши похибку прогнозу та його довірчий інтервал.

–        Побудувати поле кореляції та графік лінії регресії.

–        Додатково здійснити розрахунки по оцінці параметрів регресії за допомогою спеціалізованого інструментарію MS Excel (надбудова «Аналіз даних», функції ЛИНЕЙН(), СТЬЮДРАСПОБР(), FРАСПРОБР(), побудова лінії тренда).

–        Зробити висновки щодо взаємозв’язку факторів та адекватності побудованого регресійного рівняння.

Початкові дані:

По територіям регіону наводяться дані за 200X р..

Варіант 1

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	81	124
2	77	131
3	85	146
4	79	139
5	93	143
6	100	159
7	72	135
8	90	152
9	71	127
10	89	154
11	82	127
12	111	162

Варіант 2

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	74	122
2	81	134
3	90	136
4	79	125
5	89	120
6	87	127
7	77	125
8	93	148
9	70	122
10	93	157
11	87	144
12	121	165

Варіант 3

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	77	123
2	85	152
3	79	140
4	93	142
5	89	157
6	81	181
7	79	133
8	97	163
9	73	134
10	95	155
11	84	132
12	108	165

Варіант 4

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	83	137
2	88	142
3	75	128
4	89	140
5	85	133
6	79	153
7	81	142
8	97	154
9	79	132
10	90	150
11	84	132
12	112	166

Варіант 5

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	79	134
2	91	154
3	77	128
4	87	138
5	84	133
6	76	144
7	84	160
8	94	149
9	79	125
10	98	163
11	81	120
12	115	162

Варіант 6

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	92	147
2	78	133
3	79	128
4	88	152
5	87	138
6	75	122
7	81	145
8	96	141
9	80	127
10	102	151
11	83	129
12	94	147

Варіант 7

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	75	133
2	78	125
3	81	129
4	93	153
5	86	140
6	77	135
7	83	141
8	94	152
9	88	133
10	99	156
11	80	124
12	112	156

Варіант 8

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	69	124
2	83	133
3	92	146
4	97	153
5	88	138
6	93	159
7	74	145
8	79	152
9	105	168
10	99	154
11	85	127
12	94	155

Варіант 9

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	78	133
2	94	139
3	85	141
4	73	127
5	91	154
6	88	142
7	73	122
8	82	135
9	99	142
10	113	168
11	69	124
12	83	130

Варіант 10

Номер регіону	Середньодушовий прожитковий мінімум в день одного працездатного, грн.,	Середньодобова заробітна платня, грн.,
1	97	161
2	73	131
3	79	135
4	99	147
5	86	139
6	91	151
7	85	135
8	77	132
9	89	161
10	95	159
11	72	120
12	115	160

 

КОНТРОЛЬНІ ПИТАННЯ

1.          1.         Навести загальний вигляд теоретичного та емпіричного рівнянь парної лінійної регресії, перелічити їх складові елементи.

2.          Описати причини, які спонукають появу випадкової складової e в регресійних моделях.

3.          Перелічити етапи побудови економетричної моделі.

4.          Описати сутність кореляційного та регресійного аналізу. Навести відповідні формули.

5.          Розкрити сутність дисперсійного аналізу. Навести відповідні формули.

6.          Описати параметри моделі парної лінійної регресії, їх сутність та оцінювання.

7.          Охарактеризувати метод найменших квадратів: сутність і використання. Навести відповідні формули.

8.          Описати властивості оцінок на підставі методу найменших квадратів.

9.          Розкрити сутність умов Гаусса-Маркова.

10.       Описати алгоритм побудови довірчих інтервалів із заданою надійністю g для параметрів  і функції регресії . Навести відповідні формули.

11.      Охарактеризувати побудову точкового та інтервального прогнозу залежної змінної в моделі парної лінійної регресії. Навести відповідні формули.

12.      Схема перевірки гіпотез стосовно коефіцієнтів лінійного рівняння регресії.

13.       Коефіцієнт кореляції R: формули для обчислення та  сутність.

14.       Коефіцієнт детермінації : формули для обчислення та  сутність.

15.       Критерій Стьюдента. Описати алгоритм перевірки на статистичну значущість  та r в моделі парної лінійної регресії. Навести відповідні формули.