План
1. Теплоємність.
2. Коефіцієнт теплопровідності.
3. Коефіцієнт температуропровідності.
1. Теплоємність.
Повна інформація про вологі матеріали передбачає знання не тільки їх теплофізичних характеристик і параметрів (теплоємність С, коефіцієнти теплопровідності 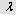 і термопровідності
і термопровідності 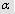 ), але й такі, як кількість теплоти, яка виділяється чи споживається при фізико–хімічних процесах, а також параметри і функції стану системи (тиск, об’єм, температура, ентальпія і інше).
), але й такі, як кількість теплоти, яка виділяється чи споживається при фізико–хімічних процесах, а також параметри і функції стану системи (тиск, об’єм, температура, ентальпія і інше).
Вивчення вказаних характеристик і параметрів у взаємозв’язку є важливими даними для науково-технічних завдань збереження сільськогосподарської продукції.
Питома теплоємність вологого матеріалу (вимірюється в Дж/кг•к) розраховується як середньозважувана величина між теплоємністю сухої речовини Сс.реч. і теплоємністю води Св, яка приймається рівною 4,19 кДж/кг•К:
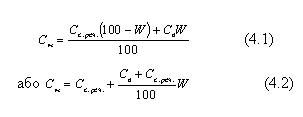
Теплоємність сухої речовини різних матеріалів становить 1257-1676 Дж/кг•к або 0,3-0,4 ккал/(кгoС).
Якщо теплоємність вологого матеріалу віднести до кілограма сухої речовини, то отримаємо теплоємність в Дж/ (кг с.реч. •К):
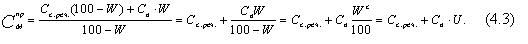
Згідно з формулами, залежність між теплоємністю матеріалу і його вологістю має лінійний характер. Але при проведенні спеціальних досліджень було встановлено, що на прямих існують переломні точки для деяких матеріалів.
Появу таких переломних точок на графіках См = f(W) пояснюється двома причинами:
– фізико-хімічними змінами сухої речовини матеріалу в різних інтервалах вологості;
– впливом таких факторів, як пористість матеріалу, наявність повітря у твердому скелеті, співвідношення між водою, яка знаходиться в рідкому і пароподібному стані та інше.
Але вплив вказаних факторів на теплоємність матеріалу є незначним. Суттєвий вплив вони мають лише на теплопровідність вологого матеріалу. Велике значення для теплоємності можуть мати внутрішні процеси, які відбуваються у разі зволоження чи сушіння матеріалу.
2. Коефіцієнт теплопровідності.
Перенесення тепла у вологих матеріалах суттєво відрізняється від передачі тепла в сухих матеріалах:
а) волога впливає на теплопровідність твердого скелета пористого тіла, в порах якого вона знаходиться;
б) перенесення тепла тісно пов’язане з безпосереднім перенесенням вологи в середині матеріалу.
Тепло може передаватись також конвенцією через пори, в яких знаходиться газ і рідина та випромінюванням між стінками пор. Тому розрізняють істинний і еквівалентний коефіцієнти теплопровідності.
Істинний коефіцієнт теплопровідності 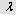 [Bm/(мК)] є коефіцієнтом пропорційності в рівнянні Фур’є
[Bm/(мК)] є коефіцієнтом пропорційності в рівнянні Фур’є

де q – щільність потоку тепла в твердому ізотропному тілі, Вт/м2;
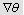 - градієнт температури, К/м.
- градієнт температури, К/м.
Еквівалентний, або ефективний коефіцієнт теплопровідності 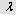 екв. характеризує здатність вологого матеріалу проводити тепло вищевказаними способами:
екв. характеризує здатність вологого матеріалу проводити тепло вищевказаними способами:
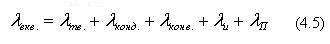
де 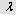 mb– коефіцієнт теплопровідності твердого скелета матеріалу;
mb– коефіцієнт теплопровідності твердого скелета матеріалу;
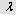 конд– коефіцієнт кондукції (теплопровідності) рідини і пароповітряної суміші, які перебувають у стаціонарному стані в порах матеріалу;
конд– коефіцієнт кондукції (теплопровідності) рідини і пароповітряної суміші, які перебувають у стаціонарному стані в порах матеріалу;
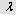 конв– коефіцієнт, який характеризує перенесення тепла конвенцією повітря всередині матеріалу;
конв– коефіцієнт, який характеризує перенесення тепла конвенцією повітря всередині матеріалу;
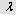 u– коефіцієнт, який характеризує перенесення тепла за рахунок перенесення маси води всередині матеріалу (у вигляді рідини та у вигляді пари);
u– коефіцієнт, який характеризує перенесення тепла за рахунок перенесення маси води всередині матеріалу (у вигляді рідини та у вигляді пари);
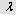 П– коефіцієнт променевої теплопровідності.
П– коефіцієнт променевої теплопровідності.
З врахуванням останнього виразу

Встановлено, що при діаметрі пор менше 0,5 мм променевим теплообміном можна нехтувати, а при діаметрах пор менших 5 мм і 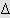
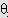 =10oC - також конвективним теплообміном.
=10oC - також конвективним теплообміном.
Для пористих матеріалів інтерес становить залежність коефіцієнта 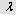 екв. від двох взаємопов’язаних факторів – діаметра пори d i пористості матеріалу або його щільності p. Чим вище щільність матеріалу, тим більше
екв. від двох взаємопов’язаних факторів – діаметра пори d i пористості матеріалу або його щільності p. Чим вище щільність матеріалу, тим більше 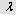 екв.. Відповідно чим більший розмір частин, який утворює скелет зернового матеріалу, тим більше
екв.. Відповідно чим більший розмір частин, який утворює скелет зернового матеріалу, тим більше 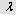 екв..
екв..
Вплив форми частин у двохфазній системі (дисперсний матеріал – повітря) на коефіцієнт теплопровідності знаходять відображення у формулі, отриманій за принципом електротеплової аналогії (теорії Максвела – Бургера – Еймена):
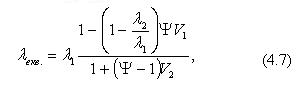
де 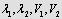 - коефіцієнт теплопровідності і об’єми твердої і газової фаз.
- коефіцієнт теплопровідності і об’єми твердої і газової фаз.
Коефіцієнт  залежить від форми частин.
залежить від форми частин.
Для кулькових зерен

Для зерен циліндричної форми
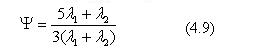
Для зерен у формі тонких пластин
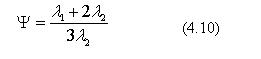
Точність результатів, отриманих за вказаними формулами залежить від правильності вибраної моделі відповідно реальній структурі матеріалу.
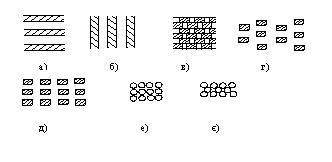
Рисунок 7.1 - Моделі зернистого матеріалу:
• необмежені пластини, а-перпендикулярні; в-паралельні тепловому потоку;
• система брусків при П<50% (в) і П>50% (г);
• система кубів (д);
• тетраїдна рихла (е) і щільна (є).
Існують і інші формули визначення 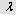 екв.. Крім цього, замість пористості в розрахункові формули вводять щільність (об’ємну масу) системи p . Зв’язок між ними встановлюється через щільність твердої фази тв:
екв.. Крім цього, замість пористості в розрахункові формули вводять щільність (об’ємну масу) системи p . Зв’язок між ними встановлюється через щільність твердої фази тв:
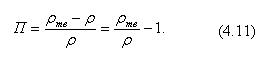
Вплив вологості матеріалу W на 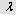 екв. обумовлена ступенем дисперсності матеріалу (крупно-, середньо-, дрібнодисперсні). У межах малої вологості матеріалу ріст
екв. обумовлена ступенем дисперсності матеріалу (крупно-, середньо-, дрібнодисперсні). У межах малої вологості матеріалу ріст 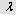 екв. відображається лінійно, причому швидкість зростання тим більше, чим крупність частинки зерен.
екв. відображається лінійно, причому швидкість зростання тим більше, чим крупність частинки зерен.
При великій вологості матеріалу ріст  екв. поступово, призупиняється (для крупнозернистих), залишається лінійним (для середньозернистих) і різко зростає (для дрібнозернистих).
екв. поступово, призупиняється (для крупнозернистих), залишається лінійним (для середньозернистих) і різко зростає (для дрібнозернистих).
Приймається, що спочатку (при малій вологості матеріалу) волога заповнює дрібні пори між зернами, після цього насичена волога переходить у повітряні пори і накопичується в основному в місцях стику зерен. Таким чином, при малій вологості система в основному складається у повітряних пор і твердого скелета; при великій вологості волога заповнює весь міжзерновий простір і повністю насичує їх.
Користуючись модельним тілом, можна розглянути поведінку капілярної рідини при різному заповненні пор. В точці контакту частин в міру надходження рідини утворюється накопичення рідини, яка має форму подвійної ввігнутої лінзи.
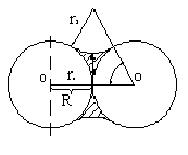
Рисунок 7.2 - Рідинна манжета (стикова рідина) між двома сферичними частинами
Середня кривизна такої поверхні рівна 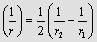 при r2 < r1. Радіуси кривизни при певному змочуванні залежать від радіуса частин R і кута
при r2 < r1. Радіуси кривизни при певному змочуванні залежать від радіуса частин R і кута 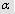 . Таке накопичення рідини називають рідинною манжетою, а рідину – стиковою.
. Таке накопичення рідини називають рідинною манжетою, а рідину – стиковою.
Капілярний тиск стикової рідини буде рівний
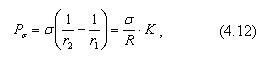
де К – деяка постійна, яка залежить тільки від кута 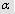 . Якщо рідини мало, то вона розподілена дискретними розділеними кільцями. Якщо розміри частин незначні, то із збільшення надходження рідини манжети поступово збільшуються і зливаються між собою. Таке злиття відбувається при куті
. Якщо рідини мало, то вона розподілена дискретними розділеними кільцями. Якщо розміри частин незначні, то із збільшення надходження рідини манжети поступово збільшуються і зливаються між собою. Таке злиття відбувається при куті 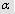 =30o.
=30o.
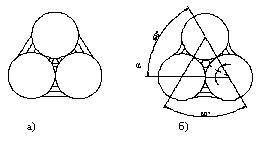
Рисунок 7.3 - Перехід від стикового стану до канатного:
а - защемлена вода, б – защемлене повітря
Канатним станом рідини називається такий стан, коли рідка плівка неперервно розміщена навколо тіла. Капілярний стан відрізняється від канатного наявністю хоча б однієї вільної поверхні для утворення меніска капіляра.
3. Коефіцієнт температуропровідності.
Коефіцієнт температуропровідності 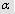 є важливою характеристикою матеріалу, який визначає його теплоінерційні властивості; чим вище
є важливою характеристикою матеріалу, який визначає його теплоінерційні властивості; чим вище 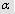 , тим швидше відбувається нагрівання і охолодження матеріалу. Тому коефіцієнт
, тим швидше відбувається нагрівання і охолодження матеріалу. Тому коефіцієнт 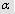 необхідно враховувати при дослідженні і розрахунку нестаціонарних процесів – нагрівання, охолодження, сушіння, зволоження та інших.
необхідно враховувати при дослідженні і розрахунку нестаціонарних процесів – нагрівання, охолодження, сушіння, зволоження та інших.

де 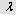 - коефіцієнт теплопровідності матеріалу;
- коефіцієнт теплопровідності матеріалу;
С – питома теплоємність;
p - щільність (об’ємна маса).
Добуток Cp - це теплоємність одиниці об’єму матеріалу. Вона характеризує теплоакумулюючу здатність; чим більше Cp , тим при такому ж значенні 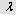 , коефіцієнт
, коефіцієнт 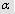 буде меншим.
буде меншим.
Аналогічно еквівалентному коефіцієнту теплопровідності матеріалу можна ввести еквівалентний коефіцієнт температуропровідності 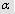 екв. Тоді диференційне рівняння внутрішнього тепла буде мати вигляд:
екв. Тоді диференційне рівняння внутрішнього тепла буде мати вигляд:
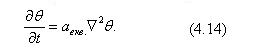
Загалом характер зміни параметрів тіла в процесі теплового зневоднення матеріалом розглядає кінетика процесу.
Під кінетикою процесу розуміють зміну середнього вологовмісту 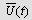 і середньої температури тіла
і середньої температури тіла 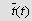 .
.
Знаходження полів вологовмісту U = (X, Y, Z,  ) пов’язано із рішенням диференційних рівнянь масо- і теплоперенесення за відповідних граничних умов. Ця система є системою нелінійних диференціальних рівнянь, тому їх вирішують з допомогою ЕОМ.
) пов’язано із рішенням диференційних рівнянь масо- і теплоперенесення за відповідних граничних умов. Ця система є системою нелінійних диференціальних рівнянь, тому їх вирішують з допомогою ЕОМ.
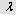 і термопровідності
і термопровідності 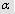 ), але й такі, як кількість теплоти, яка виділяється чи споживається при фізико–хімічних процесах, а також параметри і функції стану системи (тиск, об’єм, температура, ентальпія і інше).
), але й такі, як кількість теплоти, яка виділяється чи споживається при фізико–хімічних процесах, а також параметри і функції стану системи (тиск, об’єм, температура, ентальпія і інше).
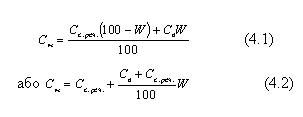
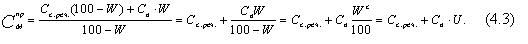

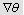 - градієнт температури, К/м.
- градієнт температури, К/м.
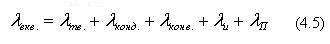

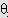 =10oC - також конвективним теплообміном.
=10oC - також конвективним теплообміном.
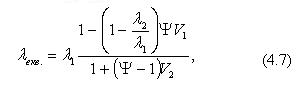
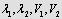 - коефіцієнт теплопровідності і об’єми твердої і газової фаз.
- коефіцієнт теплопровідності і об’єми твердої і газової фаз.
 залежить від форми частин.
залежить від форми частин.

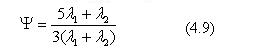
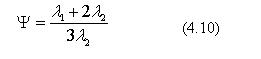

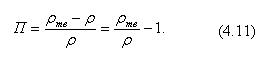

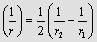 при r2 < r1. Радіуси кривизни при певному змочуванні залежать від радіуса частин R і кута
при r2 < r1. Радіуси кривизни при певному змочуванні залежать від радіуса частин R і кута 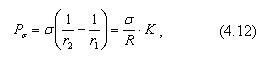


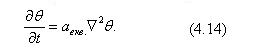
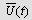 і середньої температури тіла
і середньої температури тіла 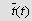 .
.
 ) пов’язано із рішенням диференційних рівнянь масо- і теплоперенесення за відповідних граничних умов. Ця система є системою нелінійних диференціальних рівнянь, тому їх вирішують з допомогою ЕОМ.
) пов’язано із рішенням диференційних рівнянь масо- і теплоперенесення за відповідних граничних умов. Ця система є системою нелінійних диференціальних рівнянь, тому їх вирішують з допомогою ЕОМ.