Тема 3-4. Умовна ентропія

План

1.    Поняття про умовну ймовірність

2.    Модель системи передачі інформації

3.    Види умовної ентропії

4.    Ентропія об'єднання двох джерел інформації

 

1.    Поняття про умовну ймовірність

Раніше отримана формула ентропії (2.4) визначає її середньою кількістю інформації, що припадає на одне повідомлення джерела статистично незалежних повідомлень. Така ентропія називається безумовною.

Як відомо з відповідного розділу математичної статистики, мірою порушення статистичної незалежності повідомлень x і у є умовна ймовірність p(x/y) появи повідомлення x_i за умови, що вже вибрано повідомлення y_j або умовна ймовірність появи повідомлення y_j, якщо вже отримане повідомлення x_i, причому в загальному випадку p(x/y)¹p(y/x).

Умовну ймовірність можна отримати з безумовної ймовірності p(x) чи p(y) та сумісної ймовірності системи в. в. p(x, y) за формулою множення ймовірностей:

 

p(x, y)=p(x)×p(y/x),                                          (3.1)

 

p(x, y)=p(y)×p(y/x),                                           (3.2)

 

звідси

,

.

В окремому випадку для статистично незалежних повідомлень маємо: p(y/x)=p(y),  p(x/y)=p(x).

При існуванні статистичної залежності між повідомленнями джерела факт вибору одного з повідомлень зменшує або збільшує ймовірності вибору інших повідомлень до умовних ймовірностей. Відповідно змінюється й кількість інформації, що міститься в кожному з цих повідомлень, згідно з (1.2). Ентропія такого джерела також змінюється відповідним чином, причому обчислюється ентропія за тією самою формулою (1.3), але вже з урахуванням умовних ймовірностей. Така ентропія називається умовною.

2.    Модель системи передачі інформації

Розглянемо модель системи спостереження, перетворення, збору і зберігання інформації, що складається з двох джерел, між повідомленнями яких існує статистичний взаємозв'язок. Нехай джерело X задано моделлю - ансамблем повідомлень {x₁, x₂, …, x_i, …, x_k} і рядом розподілу P(X) їхніх ймовірностей, а джерело Y - ансамблем {y₁, y₂, …, y_j, …, y_l} і розподілом P(Y).

Ніяких обмежень на алфавіти X і Y не накладається. Вони можуть навіть збігатися (X=Y). Тоді можна аналізувати і враховувати взаємозв'язок між повідомленнями одного джерела, що рознесені за часом. Найбільш поширеною такою моделлю є послідовності елементарних повідомлень {x_i}, умовна ймовірність p(x_i/x_i-1) кожного з яких залежить тільки від попереднього значення x_i-1 за умови появи всіх i-1 повідомлень. Такі послідовності називають ланцюгами Маркова.

Алфавіти X і Y можуть і не збігатися (X¹Y), хоча між їхніми елементами може бути встановлена взаємна відповідність. Джерело X описується моделлю - ансамблем повідомлень {x_i} і рядом розподілу P(X). У той самий час джерело X може виступати як об'єкт спостереження для одержувача інформації Y і разом з ним утворювати нове джерело, яке описується моделлю - ансамблем {y_j} і розподілом P(Y). Між джерелом X і спостерігачем Y існує канал зв'язку, на який впливають завади, що можуть порушити процес вибору спостерігачем Y повідомлень алфавіту y_jÎY, що, у свою чергу, порушує відповідність між повідомленнями x_iÎX і y_jÎY.

Алфавіти X і Y можуть бути однакового (k=l) і неоднакового (k¹l) об'ємів. Звичайно розглядаються ситуації, коли k=l або  k<l. Система спостереження при k=l має природне пояснення. Спостерігач Y повинен реагувати повідомленнями y_j (j=1, ..., l) на кожний стан джерела X, представлений повідомленням x_i (i=1,...,k), при чому кожному повідомленню x_i джерела X відповідає повідомлення y_j з Y: x₁®y₁, x₂®y₂, …, x_i®y_i, …, x_k®y_k.

Дана модель показана на рис.1.3, за винятком елемента y_l з Y, де l=k+1 (жирними лініями показані напрями взаємооднозначної відповідності XÛY).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

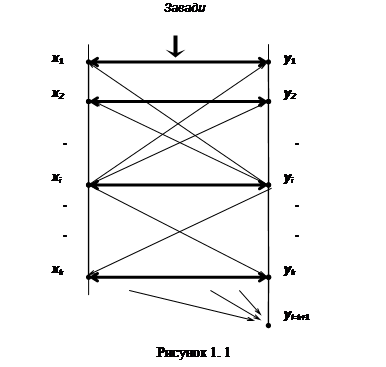
У разі, коли джерелом X вибране деяке повідомлення x_i, якому повинне відповідати повідомлення y_j при i=j, то через вплив завад джерелом Y може бути вибране будь-яке з повідомлень y_j, j=1…k з ймовірністю p(y_j/x_i), причому умовна імовірність правильного вибору повідомлення p(y_i/x_i). Інші повідомлення y_j, що визначаються умовними ймовірностями p(y_j/x_i), де i¹j, є помилковими. Така модель дозволяє досліджувати систему передачі інформації з боку спостерігача Y.

Водночас таку систему можна досліджувати з позиції об'єкта спостереження X. Для цього потрібно знати факт вибору джерелом Y деякого повідомлення y_j. Після цього можна з умовною імовірністю p(x_i/y_j) говорити, що об'єкт X знаходиться у стані x_i. Це твердження правильне при i=j або неправильне при i¹j.

Існують ситуації, коли систему ускладнюють, вибираючи l>k (частіше l=k+1, див. рис. 1.1). При цьому повідомлення y_l не відповідає ніякому з повідомлень x_i і є ознакою особливого стану спостерігача Y - стирання повідомлення.

Взагалі статистична залежність джерела Y від джерела X задається матрицею прямих переходів повідомлень x_i (i=1…k) джерела X в повідомлення y_j (j=1…k) джерела Y:

 

 

На головній діагоналі цієї матриці розташовані умовні ймовірності прямої відповідності типу x₁®y₁, x₂®y₂, …, x_k®y_k, які характеризують правильний вибір джерелом Y повідомлень (тобто відповідно до повідомлень джерела X).

Матриця (1.9) відображає вплив завад у каналі зв'язку між джерелом X і спостерігачем Y (рис.1.1). Якщо завади неістотні або відсутні, то маємо однозначну відповідність x_i®y_j з умовної імовірності p(y_i/x_i)=1 для i=1…k, решта ймовірностей p(y_i/x_i)=0 для всіх i¹j.

Кожний рядок в (1.9) є спотвореним розподілом ймовірностей p(y_j/x_i) появи повідомлень y_jÎY, причому для кожного рядка повинна виконуватися умова нормування

 

.                                              (3.3)

 

Статистична залежність джерела X від джерела Y подається матрицею зворотних переходів типу x_i¬y_j з умовних ймовірностей p(x_i/y_j):

 

         

Матриця (1.11) складається з k розміщених стовпцями варіантів первинних розподілів ймовірностей ансамблю X, що на собі відчуває статистичний вплив повідомлень y_j джерела Y. Для кожного такого розподілу виконується умова нормування

 

 .                                 (3.4)

 

Отже, якщо задані ансамбль X і матриця прямих переходів (1.9), то, використовуючи безумовні імовірності P(X)={p(x_i)}, за формулою (1.7) можна знайти матрицю сумісних ймовірностей

 

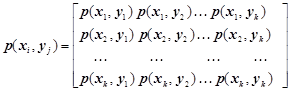.                          (3.5)

 

Виконавши у (3.5) згортку за i, дістанемо ряд розподілу безумовних ймовірностей P(Y)={p(y_j)}, j=1…k:

 

,                                                  (3.6)

 

а виконавши згортку за j, - розподіл P(X)={p(x_i)}, i=1…k:

.                                                (3.7)

 

 

 

3.    Види умовної ентропії

Вирізняють часткову та загальну умовні ентропії джерела повідомлень.

Часткова умовна ентропія - це кількість інформації, що припадає на одне повідомлення джерела X за умови встановлення факту вибору джерелом Y повідомлення y_j, або кількість інформації, що припадає на одне повідомлення джерела Y за умови, що відомий стан джерела X:

 

,              (3.8)

 

 ,            (3.9)

 

де , - алфавіти повідомлень; x_i - певне повідомлення джерела X, щодо якого визначається часткова умовна ентропія H(Y/x_i) алфавіту Y за умови вибору джерелом X повідомлення x_i; y_j - певне повідомлення джерела Y, щодо якого визначається часткова умовна ентропія H(X/y_j) алфавіту X за умови вибору повідомлення y_j; i - номер повідомлення з алфавіту X; j - номер повідомлення з алфавіту Y; p(x_i/y_j), p(y_j/x_i) – умовні імовірності.                        

Загальна умовна ентропія визначається так:

 

,                                         (3.10)

 

.                                          (3.11)

 

Отже, загальна умовна ентропія (3.10) - це середньостатистична кількість інформації (математичне сподівання), що припадає на будь-яке повідомлення джерела X, якщо відомий його статистичний взаємозв'язок з джерелом Y. Так само загальна умовна ентропія (1.19) - це середня кількість інформації, яка міститься в повідомленнях джерела Y за наявності статистичного взаємозв'язку з джерелом X.

З урахуванням (1.16), (1.17) та (1.7), (1.8) вирази (1.18), (1.19) набувають такого вигляду:

 

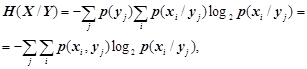,                       (3.12)

 

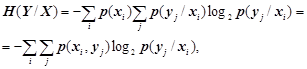,                       (3.13)

     

де p(x_i, y_j) - сумісна імовірність появи повідомлень x_i, y_j; p(x_i/y_j), p(y_j/x_i) – їх умовні імовірності.

Властивості умовної ентропії:

1)    якщо джерела повідомлень X і Y статистично незалежні, то умовна ентропія джерела X стосовно Y дорівнює безумовній ентропії джерела X і навпаки:

H(X/Y)=H(X), H(Y/X)=H(Y);

2)    якщо джерела повідомлень X і Y настільки статистично взаємозв'язані, що виникнення одного з повідомлень спричиняє безумовну появу іншого, то їхні умовні ентропії дорівнюють нулю:

H(X/Y)=H(Y/X)=0;

3)    ентропія джерела статистично взаємозалежних повідомлень (умовна ентропія) менша від ентропії джерела незалежних повідомлень (безумовної ентропії):

H(X/Y)<H(X), H(Y/X)<H(Y).

З властивості 3 випливає поняття статистичної надмірності, обумовленої наявністю статистичної залежності між елементами повідомлення:

 

,                                              (3.14)

 

де H(X/Y) - загальна умовна ентропія джерела X стосовно джерела Y; H(X) - безумовна ентропія джерела X. 

З урахуванням виразу (1.5) загальна статистична надлишковість алфавіту джерела інформації визначається так:

 

.                                              (3.15)

 

У разі малих значень ,  статистична надлишковість визначається виразом

 

.                                                            (3.16)

 

4.    Ентропія об'єднання двох джерел інформації

 

Ентропію H(X, Y) об'єднання двох джерел інформації X і Y знаходять через імовірності p(x_i, y_j) системи випадкових повідомлень x_i, y_j для всіх i=1...k, і j=1...l. Для цього складається матриця ймовірностей системи двох статистично залежних джерел

 

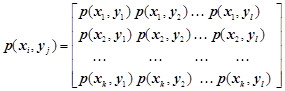.                      (3.17)

 

Ентропія об'єднання двох джерел H(X, Y) (взаємна ентропія) - це середня кількість інформації, що припадає на два будь-які повідомлення джерел X і Y:

 

.                           (3.18)

 

З рівності p(x_i, y_j)= p(y_j, x_i) випливає, що

H(X, Y)=H(Y, X).

Скориставшись формулами (1.7), (1.12), запишемо вираз (1.26) так:

 

Перший доданок цього виразу відповідає безумовній ентропії H(X) (1.3), а другий - умовній H(Y/X) (1.21). Звідси

 

H(X, Y)=H(X)+H(Y/X).                                     (3.19)

 

З симетричності формул (1.7) – (1.8) випливає, що аналогічний вираз для взаємної ентропії H(X, Y) має вигляд

 

H(X, Y)=H(Y)+H(X/Y),                                            (3.20)

 

звідси

 

H(Y/X)=H(X,Y)-H(X),                                            (3.21)

 

H(X/Y)=H(X,Y)-H(Y).                                            (3.22)

 

Кількість інформації, що припадає на одне повідомлення, передане по каналу зв'язку джерелом X спостерігачу Y (рис.1.3), за наявності завад і статистичного взаємозв'язку ансамблів X і Y з урахуванням виразів (1.27), (1.28) і властивості 4 кількості інформації і ентропії знаходиться за формулою

 

I(X,Y)=H(Y)+H(X)-H(X,Y)=H(X)-H(X/Y)=H(Y)-H(Y/X).            (3.23)

 

Властивості ентропії об'єднання двох джерел інформації:

1)    при статистичній незалежності джерел X і Y їх взаємна ентропія дорівнює сумі ентропій кожного з джерел, тобто H(X, Y)=H(X)+H(Y);

2)    при повній статистичній залежності джерел X і Y їх взаємна ентропія дорівнює безумовній ентропії одного з джерел, тобто H(X,Y)=H(X)=H(Y);

3)    взаємна ентропія статистично залежних джерел X і Y менша суми безумовних ентропій кожного з них, тобто H(X, Y) £ H(X)+H(Y).