Алгоритм 1

(вирівнювання графіка електричного навантаження за допомогою споживачів-регуляторів, що мають багатоступінчаті графіки навантаження)

1. Визначаємо  сумарного графіка навантаження.

2. Визначаємо площі піків (ті частини графіків, які знаходяться над) – вектор,. Для першого кроку t=1.

3. Визначаємо номер того піку , площа якого є максимальною серед множини піків .

4. Визначаємо номера споживачів, що працюють в зоні даного максимального піку .  – множина споживачів по яких може вестись оптимізація для даного піку.

5. Визначаємо для множини  коефіцієнти кореляції між графіками навантаження споживачів і сумарним графіком навантаження споживачів-регуляторів – множина .

6. Визначаємо з множини  споживач з максимальним коефіцієнтом кореляції –.

7. Здійснюємо здвиг споживача  таким чином, щоби мінімізувати середньоквадратичне відхилення –.

А. Якщо  сумарного графіка зменшилась переходимо до п.2.

Б. Якщо  збільшилась чи зсув споживача привів до порушення обмежень, вважаємо крок неуспішним, приводимо споживач в вихідне положення, виключаємо споживач  з множини і переходимо до пункту 5. У випадку якщо множина , переходимо до пункту 8.

8. Виключаємо пік  з множини піків  і переходимо до пункту 3. Якщо , робота алгоритму закінчується.

 

 

 

Алгоритм 2

Багатокритерійна постановка задачі

Вищезгадані методи оптимізації не завжди є ефективні, оскільки у більшості випадків вирівнювання графіка навантаження може призвести до збільшення витрат електричної енергії і до збільшення собівартості продукції, що випускається.

Будь-яка система енергетики, характеризується множиною особливостей і властивостей. Розкрити переваги врахування більшої кількості істотних властивостей системи енергетики можливо при використанні багатокритерійної (векторної) оптимізації. Це дозволить в основу оптимізації крім задачі вирівнювання графіка електричного навантаження закласти і зменшення витрат і втрат електричної енергії на підприємстві та багато інших критеріїв, що дозволить ліквідувати недоліки виявлені при використанні вищезгаданих критеріїв.

Точних методів розв’язку задач багатокритерійної оптимізації в даний час не існує, що пов’язано з тим, що в якості критерію виступає не скаляр, а вектор і задача полягає в одночасній екстремізації всіх критеріїв (цільових функцій).

Отже, постає задача багатокритерійної оптимізації, в якій нечітко описана множина альтернатив і чітко функції корисності (цільові функції). Це є типова задача нечіткого математичного програмування (НМП).

Задача НМП формулюється, як задача виконання нечітко визначеної цілі, причому розв’язками є перетини нечітких множин цілі і обмежень.

Задача досягнення нечітко визначеної цілі, що сформульована Беллманом-Заде, побудована на припущенні, що ціль прийняття рішень і множина альтернатив розглядаються як рівноправні нечіткі підмножини деякої універсальної множини альтернатив.

В нашому випадку, для поставленої нами задачі, таке припущення буде справедливим. І оскільки дане припущення значно спрощує процес реалізації алгоритму оптимізації то доцільно скористатись підходом Беллмана-Заде для розв’язку поставленої задачі.

При використанні підходу Беллмана-Заде кожній з цільових функцій , , , вихідної багатокритерійної задачі повинна бути поставлена у відповідність нечітка цільова функція (нечітка множина):

, , ,

де ­– функція приналежності нечіткої множини до множини оптимальних розв’язків.

Розв’язок вихідної багатокритерійної задачі приводиться до знаходження

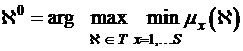.                             (1.1)

Для того щоб перейти до розв’язку задачі багатокритерійної оптимізації необхідно побудувати відповідні функції приналежності.

Існує дві групи методів побудови функцій приналежності: прямі і непрямі (посередні). Прямі методи визначаються тим, що експерт безпосередньо задає правила визначення значень функції приналежності . В непрямих (посередніх) методах значення функції приналежності вибирається таким чином, щоб задовольнити раніше сформульовані вимоги. Крім цього методи побудови функцій приналежності можна розбити ще на дві категорії: методи одного експерта і методи групи експертів.

Розв’язок задачі багатокритерійної оптимізації розглядається як нечітка підмножина значень цільових функцій наступним чином: нехай – цільові функції і необхідно розв’язати задачу  для всіх ; нехай – множина цільових функцій, тоді будь-яке значення  в області визначення  можна розглядати як нечітку множину на  з вектором значень приналежності  .

Для функцій, що максимізуються функції приналежності:

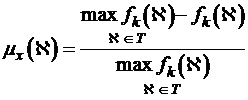.                                    (1.2)

Легко бачити, що для функцій, які мінімізуються (1.2) можна привести до наступного вигляду:

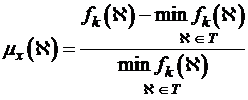.                                    (1.3)

При врахуванні різної важливості цільових функцій , , , можна “деформувати” функції приналежності (1.2) і (1.3). Ця деформація” досягається в результаті використання замість них відповідно функцій приналежності:

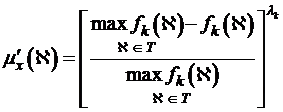,                                       (1.4)

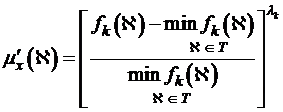,                                       (1.5)

де коефіцієнт важливості відповідної цільової функції.

За побудованими функціями приналежності  за допомогою (1.1) можна легко знайти максимальну степінь приналежності нечіткому розв’язку і найбільш доцільний час ввімкнення споживача-регулятора.