Приклад 3.1.  Для групи з трьох електроприймачів  a, b, c  графіки яких ,  наведені в табл.3.1, визначити оптимальні зрушення в часі , що дозволяють максимально вирівняти графік суміщеного навантаженням    

Таблиця 3.1 - Вихідні графіки навантаження

 

Розв'язок

Виконуємо розрахунок ВКФ  графіків навантажень електроприймачів  a і b:

1. Визначаємо квадрат середньої потужності  і середньоквадратичних потужностей  графіків  і , а також графіка їх сумісного навантаження  побудованого при різних зрушеннях .

2. Для графіка   

,.

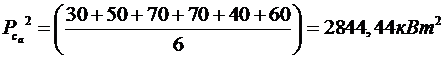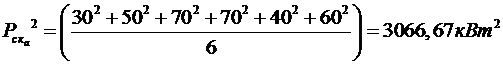Для графіків  і  розрахунок виконується аналогічно.

3. За виразом (3.1) розраховуються значення дисперсій ,  вихідних графіків навантаження  і , а також дисперсія  суміщеного графіка навантаження  при різних зрушеннях .

Для графіка

Для графіків  і  розрахунок виконується аналогічно.

4. За виразом (3.5) виконується розрахунок значень ВКФ :

При  зсуві

.

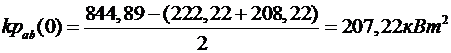Для інших зрушень розрахунок виконується аналогічно.

5. Аналогічно виконується розрахунок ВКФ . Результати розрахунків дисперсій і значень ВКФ всіх пар графіків навантаження наведено в таблицях 3.2-3.4.

Таблиця 3.2 - Розрахунок ВКФ графіків навантаження  і

Інтер-вал	Потужність, кВт		Зсув
i			0	1	2	3	4	5
1	30	20	50	70	90	90	60	80
2	50	35	85	105	105	75	95	65
3	70	63	133	133	103	123	93	113
4	70	57	127	97	117	87	107	127
5	40	37	77	97	67	87	107	107
6	60	48	108	78	98	118	118	88
	2844,44	1877,78	9344,44	9344,44	9344,44	9344,44	9344,44	9344,44
	3066,67	2086,00	10189,33	9752,67	9586,00	9652,67	9682,67	9786,00
	222,22	208,22	844,89	408,22	241,56	308,22	338,22	441,56
			207,22	-11,11	-94,44	-61,11	-46,11	5,56

 

Таблиця 3.3 - Розрахунок ВКФ графіків навантаження  і

Інтер-вал	Потужність, кВт		Зсув
i			0	1	2	3	4	5
1	30	10	40	60	80	80	50	70
2	50	15	65	85	85	55	75	45
3	70	7	77	77	47	67	37	57
4	70	13	83	53	73	43	63	83
5	40	3	43	63	33	53	73	73
6	60	12	72	42	62	82	82	52
	2844,44	100,00	4011,11	4011,11	4011,11	4011,11	4011,11	4011,11
	3066,67	116,00	4279,33	4216,00	4349,33	4216,00	4252,67	4182,67
	222,22	16,00	268,22	204,89	338,22	204,89	241,56	171,56
			15,00	-16,67	50,00	-16,67	1,67	-33,33

 

Таблиця 3.4 - Розрахунок ВКФ графіків навантаження  і

Інтер-вал	Потужність, кВт		Зсув
i			0	1	2	3	4	5
1	20	10	30	45	73	67	47	58
2	35	15	50	78	72	52	63	35
3	63	7	70	64	44	55	27	42
4	57	13	70	50	61	33	48	76
5	37	3	40	51	23	38	66	60
6	48	12	60	32	47	75	69	49
	1877,78	100,00	2844,44	2844,44	2844,44	2844,44	2844,44	2844,44
	2086,00	116,00	3066,67	3055,00	3151,33	3062,67	3054,67	3021,67
	208,22	16,00	222,22	210,56	306,89	218,22	210,22	177,22
			-1,00	-6,83	41,33	-3,00	-7,00	-23,50

 

Для подальшого аналізу значення ВКФ ,   зведені в табл. 3.5.

 

Таблиця 3.5 - Значення ВКФ графіків навантаження при різних зрушеннях

 

Далі розрахунок ведемо згідно з наведеним вище алгоритмом.

1. З графіків ВКФ видно, що максимально негативне значення має ВКФ графіка  при зсуві . Отже, на осі часу фіксуємо зрушення , яке відповідає найбільшому від'ємному значенню з усіх ВКФ.

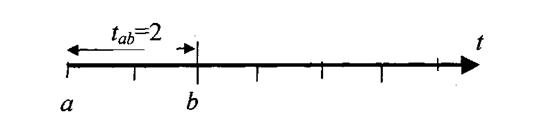
2. Так як взаємокореляційні функції  розраховувалися виходячи із зміщення графіка  щодо графіків  і , то початок графіка навантаження електроприймача с розміщуємо на осі часу правіше моментів включення електроприймачів а і b.

3. З утворених зрушень  будемо вважати незалежним зрушення . Тоді зсув  буде залежним і визначатиметься за наступним виразом:

4. Переймаючись значеннями незалежного зсуву , визначаємо можливі значення залежного зсуву .

При           ,

При            .

Для інших значень зсуву  розрахунок виконується аналогічно.  

5. Для поточної групи електроприймачів а , b і с представленої на осі часу, визначаємо безліч сум взаємокореляційних моментів для кожного значення незалежного зсуву .

При  і при       

Для інших поєднань зрушень  і   розрахунок виконується аналогічно. Результати розрахунків залежного зсуву , значення ВКФ при відповідних зрушення та їх сумарне значення зводимо в таблицю:

 

 

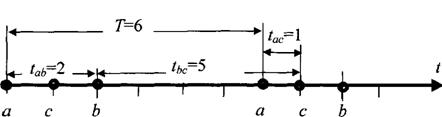
З таблиці видно, що сума  має найбільш негативне значення при зрушеннях  і  або (з урахуванням тривалості періоду Т = 6) .

Таким чином, оптимальним розміщенням в часі графіків навантаження електроприймачів забезпечуватиметься при наступній схемі включення їх в роботу:

За виразом (3.2) визначимо дисперсію суміщеного графіка навантаження трьох електроприймачів при оптимальних зрушеннях графіків навантаження у часі:

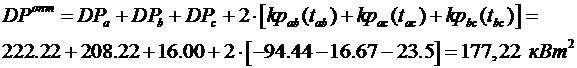
Для порівняння розрахуємо дисперсію суміщеного графіка навантаження у вихідному режимі, тобто при зрушенні .

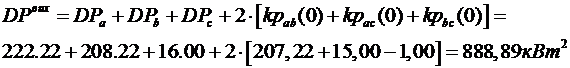
У табл.3.6 наведені графіки навантаження електроприймачів, а також суміщеного навантаження при оптимальних зрушеннях робочих циклів цих електроприймачів.

Таблиця 3.6 - Графіки навантаження при зрушеннях