Лекція 7. Реляційна алгебра

1. Реляційна алгебра.

1. Реляційна алгебра.

До складу реляційноі моделі даних, крім структури даних, мають входити операції маніпулювання даними. З усіх таких операцій складається мова запитів. 

Найбільш відомими мовами запитів у реляційній моделі є реляційна алгебра та реляційне числення (напр. мови QBE та SQL).

У класичному розумінні алгебра визначається як пара, що складається з основної множини і множини операцій (сигнатури), при цьому аргументи й результат кожної операції належать основній множині.

Реляційна алгебра є алгеброю в строгому класичному розумінні її визначення.

Елементами основної множини є реляційні відношення. У зв'язку з цим операції алгебри можуть вкладатися одна в одну, тобто аргументом певної операції може бути результат виконання іншої операції. Це дає можливість записувати запити довільного рівня складності у вигляді виразів, що містять вкладені одна в одну операції.

Сигнатура реляційної алгебри Кодда складається з восьми операцій. Перш ніж

детально розглянути ці операції, введемо поняття сумісності реляційних  відношень. Це поняття є необхідним, оскільки деякі операції (а саме: теоретико-множинні операції об'єднання, перетину та різниці) визначені лише для сумісних реляційних відношень.

Реляційні відношення  називаються сумісними, якщо:  

1) у них однакова кількість атрибутів, тобто k = n;

2) можна встановити взаємно однозначну відповідність між доменами атрибутів першої та другої реляцій, тобто домени атрибутів однакові.

Дамо також означення кількох властивостей бінарних операцій:

♦ операція φ є комутативною, якщо А φ В = В φ А;

♦ операція φ є асоціативною, якщо (А φ В) φ С = А φ (В φ C);

♦ операція φ є дистрибутивною з операцією θ, якщо А φ (В θ С) = (А φ В) θ (А φ С).

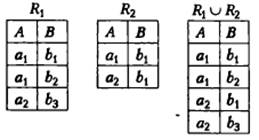
Об'єднання

Нехай L — певна множина атрибутів. Об'єднанням сумісних реляційних відношень R₁ і R₂ зі схемами R₁(L) і R₂(L) (позначається як R₁  R₂) називається таке реляційне відношення R зі схемою R(L), що містить кортежі обох поєднуваних відношень, але без повторень.

Операція комутативна, асоціативна й дистрибутивна щодо перетину.

Приклад

Перетин

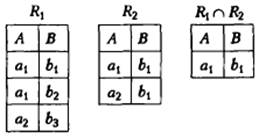
Припустимо, що L - певна множина атрибутів. Перетином сумісних реляційних відношень R₁ і R₂ зі схемами R₁(L) і R₂(L) (позначається як R₁  R₂) називається таке реляційне відношення R зі схемою R(L), яке містить кортежі, шо входять до складу обох операндів.

Операція комутативна, асоціативна й дистрибутивна щодо об'єднання.

Приклад

Різниця

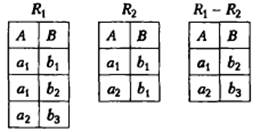
Нехай L − певна множина атрибутів. Різницею сумісних реляційних відношень R₁ і R₂ зі схемами R₁(L) і R₂(L) (позначається як R₁  R₂)  називається реляційне відношення R зі схемою R(L), що містить ті кортежі з першого операнда R₁ яких немає у другому операнді R₂.

Операція не комутативна, не асоціативна й не дистрибутивна з іншими операціями.

Приклад

Зазначимо деякі особливості теоретико-множинних операцій.

♦ У реляційній алгебрі, на відміну від алгебри множин, не використовується операція доповнення, оскільки певні домени можуть бути нескінченними або містити дуже багато значень і в результаті операції доповнення можна отримати або нескінченне відношення, або відношення з дуже великою кількістю кортежів.

♦ Вимога сумісності операндів зумовлена тим, що без цього обмеження результатом теоретико-множинних операцій могли б бути різноструктурні кортежі, а не реляційні відношення.

Розглянемо операції, які визначені лише в реляційній алгебрі.

Проекція

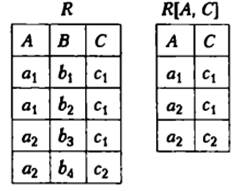
Проекцією реляційного відношення R зі схемою R(А₁,…,A_k) за атрибутами А_i1, …, А_in, де , що познається R, називається таке  відношення S зі схемою S(), кортежі якого отримані з кортежів відношення R шляхом видалення значень, що не належать атрибутам, за якими виконується проекція. При цьому в кінцевому відношенні повторні екземпляри кортежів видаляються.

Операція проекції також записується як

Приклад

Обмеження (селекція)

Спочатку дамо означення -порівнянності атрибутів. Нехай θ є одним з операторів порівняння: =, ≠, <, ≤, >, ≥ (набір операторів можна розширити). Атрибути А і В одного й того самого чи різних відношень називаються θ-порівнянними, якщо для будь-яких значень а  А і b B результат операції a θ b є визначеним (істинним або хибним). Інакше кажучи, ця операція визначена на відповідних атрибутах. Набори атрибутів L=() та М=() називаються θ-порівняними, якщо k=n і А_іθ-порівнянне з В_i(і = 1,2,..., k ). Тоді вираз LθM розуміють так:

L θ M=(A₁ θ B₁) &…& (A_k θ B_k)

Тепер дамо означення операції обмеження.

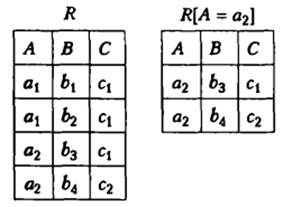
Нехай L і M - набори θ-порівнянних атрибутів схеми відношення R. Тоді обмеженням реляційного відношення R за умовою L θ M, що позначається R[L θ M], називається реляційне відношення, кортежі якого відповідають умові L θ M.

Операція обмеження також записується як σ_LθM(R).

Приклад

Декартів добуток

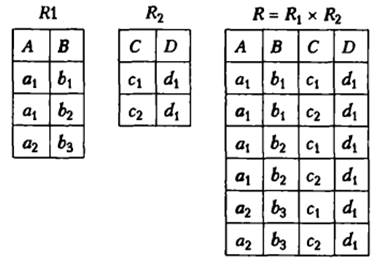
Декартовим добутком реляційних відношень R і S зі схемами R(A₁,A₂,…,A_n) та S(B₁,B₂,…,B_m) відповідно, що позначається R  S, називається відношення Q зі схемою Q(A₁,A₂,…,A_n,B₁,B₂,…,B_m), яке містить усі можливі з'єднання кортежів відношення R з кортежами відношення S:

Операція комутативна й асоціативна.

Приклад

З'єднання

Припустимо, що відношення R має схему R(L, М), а відношення S - схему S(N, Р). Нехай множини атрибутів М і N - θ-порівнянні. Тоді з'єднанням, або θ-з'єднанням, відношень R і S за умовою М θ N, що позначається як R[M θ N]S,  називається відношення Q зі схемою Q(L, М, N, Р), кортежі якого можна отримати  з'єднанням тих кортежів відношень R і S, на яких виконується умова М θ N.

Під час з'єднання атрибути, за якими виконується така операція, повторюються в кінцевому реляційному відношенні. Операція комутативна й асоціативна.

Іноді операція з'єднання позначається як S, де F - умова з'єднання.

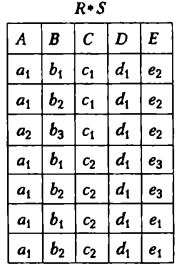
З'єднання за умовою рівності називається еквіз'єднанням. З'єднання за умовою рівності, коли один з порівнюваних атрибутів (чи група порівнюваних атрибутів) видаляється з кінцевого відношення, називається природним з'єднанням; на його позначення використовується символ «*». Наприклад, якщо задані відношення R(A, В, С, D) і S(С, D, Е), то в результаті виконання операції Q = R * S отримаємо реляцiйне відношення Q(A, В, С, D, Е).

Серед операцій θ-з'єднання виділяють операцію напівз'єднання, за якої з результату видаляються всі атрибути одного з відношень, що з'єднуються. Вона записується як R[M θ N)S.

Приклад

Ділення

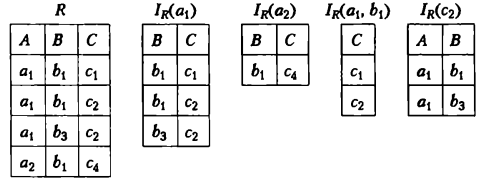
Нехай задано відношення зі схемою R(M, N). Образом реляційного відношення R за кортежем t₁  R[M] називається така множина кортежів t₂  R[N], для яких зчеплення (t₁, t₂) належить відношенню R. Образ R за кортежем t₁ позначається I_R(t₁).

Приклад

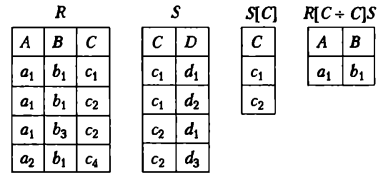
Нехай задано відношення R і S зі схемами R(M, N) та S(K, L), для яких проекції R[N] та S[K] є сумісними. Діленням відношення R на відношення S за наборами атрибутів N і К (позначається R[N÷K]S) називається операція, результатом якої є відношення Q зі схемою Q(M), що складається з таких кортежів t  R[M], образи I_R(t) яких містять усі кортежі проекції S[K].

Можна показати, шо операція ділення виражається через інші операції алгебри в такий спосіб.

R[N ÷ K]S = R[M] - ((R[M]  S[K] ) - R)[M].

Операція не комутативна й не асоціативна.

Питання для самоперевірки:

1. Що таке реляційна алгебра.

2. Реляційне числення Кодда.

3. Реляційне числення Пірота.

4. Реляційна повнота.

5. Реляційна потужність.