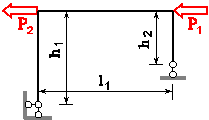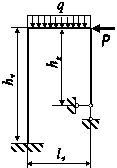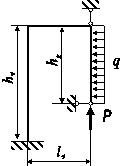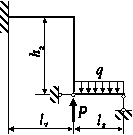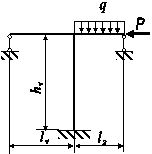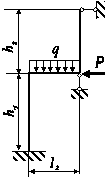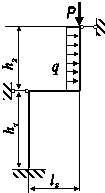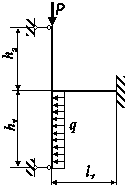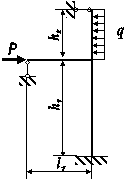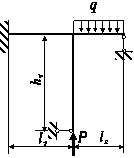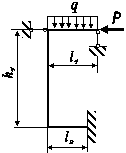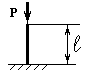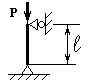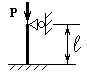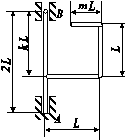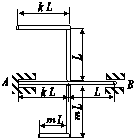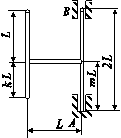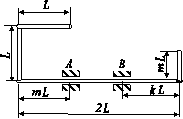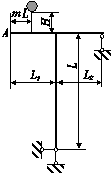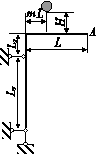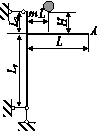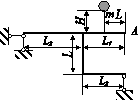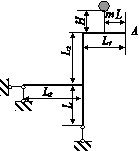Завдання для самостійної роботи студентів

Тема 1: «Осьове навантаження»

Задача 1. СТРИЖНЕВА СИСТЕМА

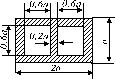
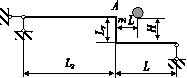
Два сталеві стрижні (1 і 2), які шарнірно сполучені в точці А, знаходяться під дією сили Р (рис. 1.1). Перший стрижень має довжину с і площу поперечного перетину F, другий - довжину а і площу - 2F.

Знайти величину нормальних напружень, що діють у стрижнях. Визначити абсолютну і відносну деформації стрижнів.

Розміри конструкції та значення навантаження вибрати з таблиці 1.1 згідно індивідуального варіанту студента.

Таблиця 1.1

Варіант	F	P	a	c	Варіант	F	P	a	c
	см^2	кН	М	м		см^2	кН	м	м
1	1.5	55	2.0	3.5	6	0.8	60	3.9	5.6
2	2.4	65	2.2	4.2	7	3.0	85	3.6	1.4
3	6.4	110	1.8	2.9	8	2.8	80	3.8	2.0
4	0.6	90	2.6	3.7	9	1.6	95	3.0	4.5
5	2.5	75	1.9	4.2	10	1.9	100	2.1	4.2

Рис. 1

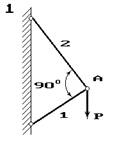
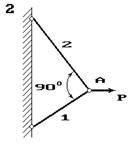
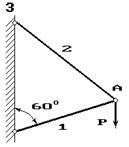
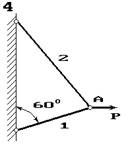
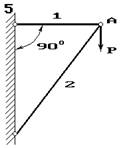
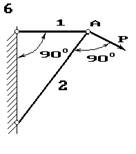
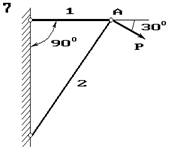
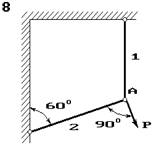
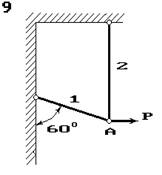
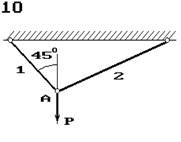
Рис.1. 1.

План розв’язання задачі

1. Розглянувши умови рівноваги шарніру А, знайти реакції в’язей.

2. Знайшовши поздовжні сили, що виникають у стрижнях, визначити нормальні напруження.

3. Абсолютні деформації знаходять за законом Гука, де модуль Юнга вибирається з додатку 5.

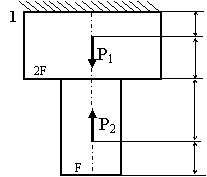
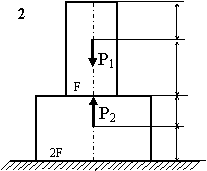
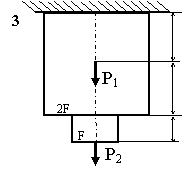
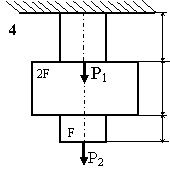
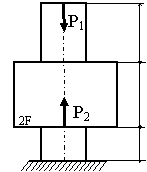
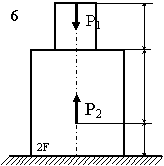
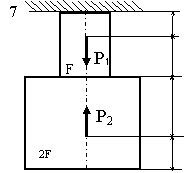
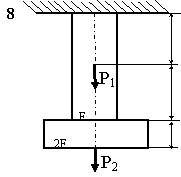
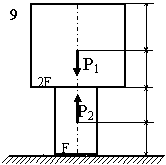
Задача 2. СХІДЧАСТИЙ сТРИЖЕНЬ

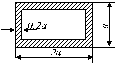
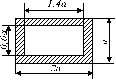
Схема а.

Для сталевого стрижня, що знаходиться під дією сил, вказаних на схемі (рис. 1.2а):

1) побудувати епюру поздовжніх сил;

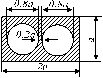
2) підібрати розміри поперечного перерізу бруса згідно критерію міцності (форма перерізу зазначена в таблиці 1. 2, а).

3) визначити напруження, що виникають в поперечних перерізах бруса та побудувати їх епюру;

4) визначити переміщення поперечних перерізів та побудувати їх епюру;

Розміри стрижня та значення навантаження вибрати з таблиці 1.2, а згідно індивідуального варіанту студента.

Таблиця 1.2, а

Варіант	P1 кН	P2 кН	a м	b м	c м	d м	Форма перерізу
1	40	20	0,7	1,1	0,8	0,5	Квадрат
2	44	38	1,2	0,5	0,4	0,9	Круг
3	35	40	1,3	0,3	1,0	0,5	Прямокутник 3
4	33	22	1,0	0,8	1,1	0,7	Еліпс 1,5
5	46	30	1,1	0,6	0,5	0,8	Прямокутник 1,5
6	30	22	1,4	0,9	0,7	0,4	Еліпс2
7	29	24	0,6	0,3	0,9	0,5	Квадрат
8	28	34	0,5	0,6	0,6	0,6	Еліпс 3
9	25	26	0,4	0,6	0,7	0,4	Круг
10	20	42	0,8	0,7	0,6	0,7	Прямокутник 2

5

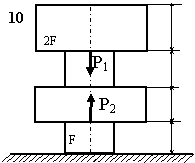
Рис. 1.2, а

План розв’язання задачі

1. Поділивши стрижень на ділянки, визначити значення поздовжніх сил.

2. З умови міцності підібрати розміри поперечних перерізів, де допустимі напруження , де — напруження, що відповідають площинці текучості (вибирається на основі додатку 1), — коефіцієнт запасу (=1,5).

3. Визначити напруження, що виникають у перерізах стрижня.

4. Переміщення поперечних перерізів знайти за законом Гука, де модуль Юнга вибирається з додатку 5.

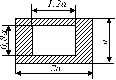
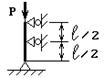
Схема б.

Для заданого ступінчастого стрижня (рис. 1.2, б) визначити розміри діаметрів поперечного перерізу на усіх ділянках, побудувати епюру нормальних напружень та поздовжніх переміщень.

При розрахунках враховувати, що , , на ділянці, де переріз має форму кільця прийняти.

Розміри стрижня та значення навантаження вибрати з таблиці 1.2, б згідно індивідуального варіанту студента.

Таблиця 1.2, б

Варіант	P1, кН	P2, кН	P3, кН	K	m	α	l, м	Матеріал
1	5	30	50	0,2	0,5	0,6	4	Сталь 10
2	-10	40	20	0,4	0,7	0,5	5	Сталь 20
3	20	-10	60	0,1	0,4	0,4	6	Сталь 25
4	15	20	-40	0,3	0,6	0,3	8	Сталь 30
5	-30	25	10	0,25	0,65	0,2	4	Сталь 35
6	25	-50	25	0,35	0,75	0,45	3	Сталь 40
7	40	15	-30	0,45	0,8	0,5	9	Сталь 45
8	20	30	50	0,15	0,6	0,35	7	Сталь 20Г
9	-50	-20	40	0,2	0,2	0,7	5	Сталь 50Г
10	60	10	-20	0,4	0,8	0,6	6	Сталь 60

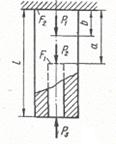
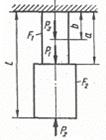
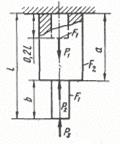
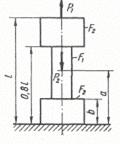
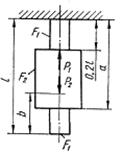
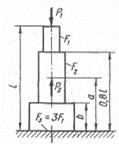
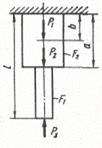
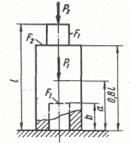
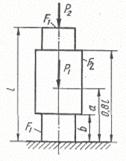
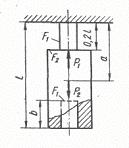Рис. 1.2, б

План розв’язання задачі

1. Зобразити розрахункову схему.

2. Побудувати епюру поздовжніх сил.

3. З умови міцності визначити діаметри стрижня на усіх ділянках, де допустимі напруження , де — напруження, що відповідають площинці текучості (вибирається на основі додатку 1), — коефіцієнт запасу (=1,5).

4. Зобразити ескіз стрижня.

5. Визначити нормальні напруження на кожній ділянці стрижня та побудувати їх епюру.

6. Обчислити абсолютну деформацію ділянок стрижня за законом Гука, де модуль Юнга вибирається з додатку 5, та побудувати епюру розподілу деформацій.

Задача 3. сТРИЖНЕВА конструкція

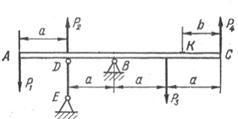
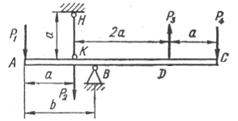
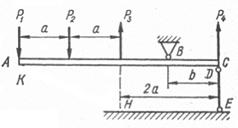
Схема а.

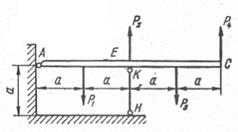
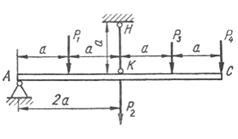
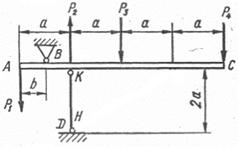
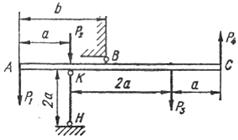
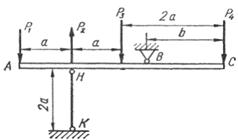
Абсолютно жорсткий брус АС опирається на шарнірно нерухому опору і прикріплений до сталевого стрижня з допомогою шарнірів (рис. 1.3, а). Визначити переміщення точок А і С, враховуючи, що стрижень має форму швелера, номер профілю та марку сталі якого вказано у таблиці 1.3, а.

Розміри стрижневої конструкції та значення навантаження вибрати з таблиці 1.3, а згідно індивідуального варіанту студента.

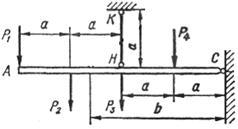
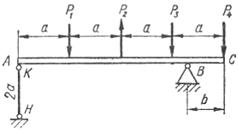Рис. 1.3, а

Таблиця 1.3, а

Варіант	P1, кН	P2, кН	P3, кН	P4, кН	Швелер	а, м	b, м	Матеріал
1	0	0	50	0	20	0,5	0,6	Сталь 10
2	0	0	0	-50	24	0,7	0,5	Сталь 20
3	0	50	0	0	20а	0,4	0,4	Сталь 25
4	50	0	0	0	16	0,6	0,3	Сталь 30
5	0	0	50	0	22	0,65	0,2	Сталь 35
6	0	-50	0	0	18а	0,75	0,45	Сталь 40
7	0	0	0	50	24	0,8	0,5	Сталь 45
8	0	0	-50	0	22а	0,6	0,35	Сталь 20Г
9	0	-50	0	0	27	0,2	0,7	Сталь 50Г
10	-50	0	0	0	18	0,8	0,6	Сталь 60

План розв’язання задачі

1. Накреслити розрахункову схему стрижневої системи.

2. З рівнянь рівноваги визначити поздовжню силу, що виникає у стрижні.

3. За законом Гука визначити деформацію стрижня, де значення модуля Юнга вибачається з додатку 5.

4. З подібності трикутників знайти переміщення точок А і С.

Схема б.

Жорсткий брус, вагою і деформаціями якого нехтуємо, підтримується системою шарнірно закріплених сталевих стрижнів (рис. 1.3, б).

Підібрати розміри (номер профілю) двотаврових стрижнів, якщо межа текучості становить 240 МПа і запас міцності k=1,5.

Для розрахунку використати дані з таблиці 1.3, б.

Таблиця 1.3, б

Варіант	Схема	Р, кН	a, м	b, м	Варіант	Схема	Р, кН	a, м	b, м
1	1	10	1,2	1,5	6	4	14	1,4	2,0
2	5	18	1,5	1,8	7	8	12	1,7	2,2
3	2	16	1,6	2,2	8	6	26	1,9	2,5
4	8	20	1,8	2,4	9	7	30	2,2	2,8
5	3	22	2,0	2,6	10	5	28	2,5	3,0

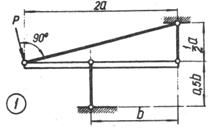
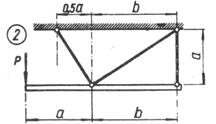
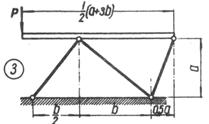
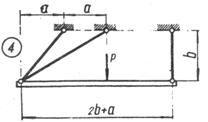
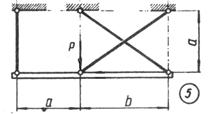
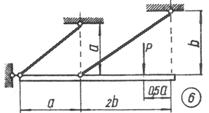
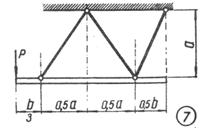
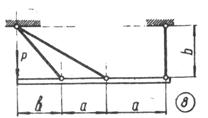
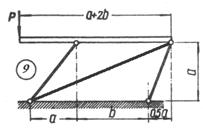
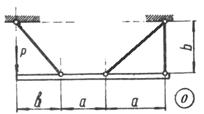
Рис. 1.3, б

План розв’язання задачі

1. Накреслити розрахункову схему стрижневої системи.

2. З рівнянь рівноваги визначити поздовжню силу, що виникає у стрижні.

3. З умови міцності визначити площі поперечних перерізів стрижнів.

За допомогою сортаменту прокатної сталі визначити номера профілів двотаврів.

Тема 2: «Розрахунки при зрізі та крученні»

Задача 1. Розрахунок заклепкових з’єднань

З умов міцності на зріз і зминання підібрати кількість заклепок (рис. 2.1) діаметром d, якщо відомі значення допустимих напружень на зріз та зминання, та вказати їх розміщення. Перевірити на міцність листи, якщо їх ширина b.

Необхідні для розрахунку дані наведені у таблиці 2.1.

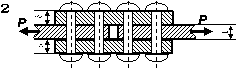
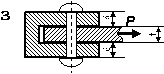
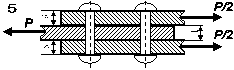
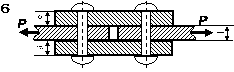
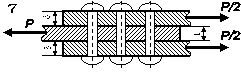
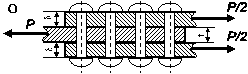
Рис. 2. 1

Таблиця 2.1.

№	d, мм	t, мм	δ, мм	b, мм	P, кН	[σзм],МПа	[τзр], МПа	Матеріал листа
1	10	6	5	220	100	300	65	Сталь 30
2	16	8	4	200	90	310	75	Сталь 40
3	8	4	5	240	95	320	70	Сталь 45
4	12	6	3	200	65	340	85	Сталь 50
5	20	10	4	220	60	350	80	Сталь 55
6	8	4	3	240	75	360	90	Сталь 60
7	8	4	2	220	85	370	100	Сталь 30Г
8	12	6	4	260	80	300	60	Сталь 50Г
9	10	5	3	200	105	340	70	Сталь 35
0	8	4	2	240	115	360	80	Сталь 30

План розв’язання задачі

1. З умови міцності на зминання визначити необхідну кількість заклепок.

2. З умови міцності на зріз розрахувати кількість заклепок.

3. Накреслити схему розміщення заклепок.

4. Перевірити лист на міцність.

Задача 2. Розрахунок зварного шва

З умови міцності розрахувати довжину флангових швів для кріплення швелера, кутника чи пластини (в залежності від вибраного варіанту (таблиця 2.21)), що виготовлені зі сталі, до фасонного листа вузла ферми (рис. 2.2) для різних типів зварювання. Для випадку кутника висоту шва прийняти рівною товщині полички, для швелера — товщині стінки, а для пластини — її висоті. Необхідні для розрахунку дані використати з таблиці 2.2.

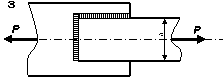
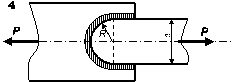
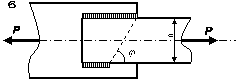
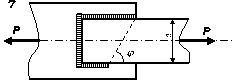
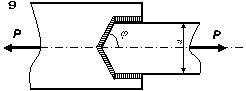
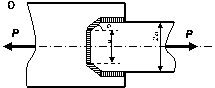
Рис. 22.2

Таблиця 2.2

№	Вид кріплення	Тип зварювання	а, мм	Матеріал листа
1	Кутник № 5(5)	Ручне, електроди з тонкою обмазкою	-	Сталь 30
2	Швелер №10	Ручне, електроди з товстою обмазкою	-	Сталь 40
3	Пластина t=3 мм	Автоматичне зварювання	200	Сталь 45
4	Кутник № 7(6)	Ручне, електроди з тонкою обмазкою	-	Сталь 50
5	Пластина t=5 мм	Ручне, електроди з товстою обмазкою	220	Сталь 55
6	Кутник № 5,6(4)	Автоматичне зварювання	-	Сталь 60
7	Пластина t=4 мм	Ручне, електроди з тонкою обмазкою	160	Сталь 30Г
8	Швелер № 12	Ручне, електроди з товстою обмазкою	-	Сталь 50Г
9	Кутник № 4(4)	Автоматичне зварювання	-	Сталь 35
0	Швелер №14	Ручне, електроди з тонкою обмазкою	-	Сталь 30

План розв’язання задачі

1. З умови міцності визначити значення допустимого навантаження.

2. З умови міцності зварного шва розрахувати його довжину..

3. Визначити довжину флангових швів.

Задача 3. Кручення валів

Схема а.

На вал, що обертається з кутовою швидкістю ω, через чотири шківи 1, 2, 3, 4 передаються потужності N1, N2, N3, N4 (рис. 2.3, а). Необхідно з умови міцності та жорсткості підібрати діаметр вала та побудувати епюру кутів закручування відносно лівого шківа.

Необхідні для розрахунку дані наведені у таблиці 2.3, а.

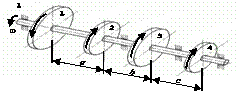
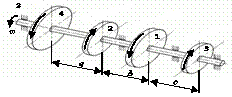
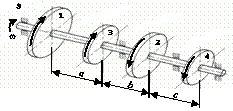
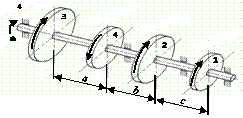
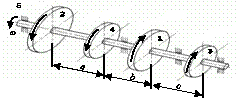
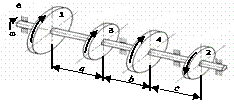
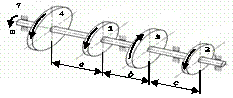
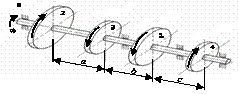
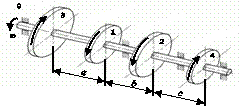
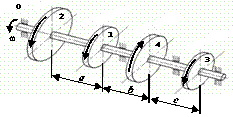
Рис. 2.3, а

Таблиця 2.3, а.

№	N1, кВт	N2, кВт	N3, кВт	N4, кВт	ω, рад/с	a, м	b, м	c, м	[τ], мПа	[θ], º/м
1	20	-	18	38	20	0,5	0,2	0,3	40	2
2	44	20	-	12	29	0,1	0,3	0,6	45	1,7
3	-	52	26	12	22	0,2	0,7	0,1	50	2
4	60	40	18	-	30	0,5	0,2	0,3	55	2,2
5	-	22	14	46	24	0,4	0,1	0,5	60	1,8
6	28	16	-	26	26	0,3	0,4	0,3	65	2
7	36	-	24	14	23	0,1	0,6	0,3	70	1,7
8	46	12	-	22	21	0,2	0,4	0,4	75	1,9
9	22	48	16	-	25	0,5	0,4	0,1	80	1,5
0	18	46	10	-	28	0,6	0,2	0,2	85	1,6

План розв’язання задачі

1. Визначити з умови рівноваги невідому потужність.

2. Розбивши вал на ділянки, визначити крутні моменти та побудувати їх епюру.

3. Визначити небезпечний переріз.

4. З умови міцності та жорсткості при крученні підібрати діаметр вала.

5. Побудувати епюру кутів закручування відносно лівого шківа.

Схема б. 

До стального валу прикладені крутні моменти: М1, М2, М3, М4, (рис. 2.3, б). Потрібно визначити діаметр вала з розрахунку на міцність та перевірити умову жорсткості при [θ]=2º/м, побудувати епюру кутів закручення.

Дані для розрахунку взяти з таблиці 2.3, б.

Таблиця 2.3, б

Номер рядка	Відстань, м			Моменти, кНм				[] МПа
	а	b	с	М1	М2	М3	М4
1	1,1	1,2	1,3	1,3	2,1	1,1	0,2	35
2	1,2	1,3	1,4	1,5	2,2	1,2	0,4	40
3	1,3	1,4	1,5	1,7	2,3	1,3	0,6	45
4	1,4	1,5	1,6	1,9	2,4	1,4	0,8	50
5	1,5	1,6	1,7	2,1	2,5	1,5	1,0	55
6	1,6	1,7	1,8	1,8	1,6	0,6	1,2	60
7	1,7	1,8	1,9	2,0	1,7	0,7	1,4	65
8	1,8	1,9	2,0	1,6	1,8	0,8	1,5	70
9	1,9	2,0	1,1	1,4	1,9	0,9	1,3	75
0	2,0	1,1	1,2	1,2	2,0	1,0	1,1	80

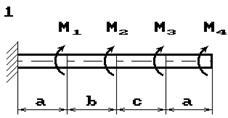
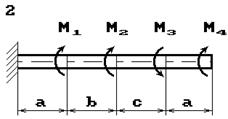
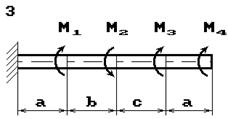
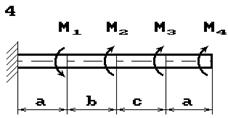
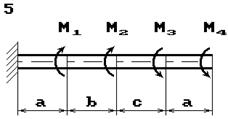
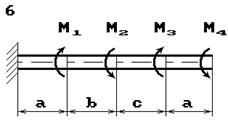
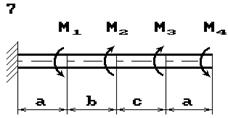
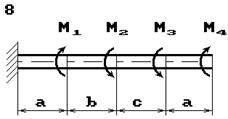
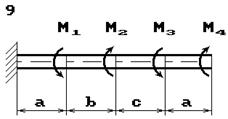
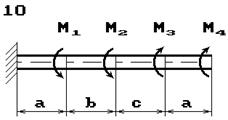
Рис. 2.3, б

План розв’язання задачі

1. Розбити вал на ділянки та побудувати епюру крутних моментів.

2. При заданому значенні [] визначити діаметр вала з розрахунку на міцність і округлити його значення до найближчої більшої, відповідно рівної: 30, 35, 40,45, 50, 60, 70, 80, 90, 100 мм.

3. Знайти найбільший відносний кут закручування та перевірити умову жорсткості при [θ]=2º/м. У випадку, якщо умова жорсткості не виконується, підібрати діаметр вала з умови жорсткості

4. Побудувати епюру кутів закручення.

Задача 4. Розрахунок гвинтових циліндричних пружин

Для заданої статично невизначної конструкції (рис. 2.4), що складається з абсолютно жорсткого бруса та системи сталевих гвинтових циліндричних пружин, визначити напруження та деформації у пружинах. Розміри конструкції, діаметри пружин та дроту, з яких вони звиті, кількість витків, навантаження задані у таблиці 2.4.

Таблиця 2.4.

№	Р, кН	а, м	b, м	c, м	n1	D1, см	d1, мм	n2	D2, см	d2, мм	n3	D3, см	d3, мм
1	10	1	0,8	0,6	6	6	5	10	5	3	8	4	6
2	15	0,8	0,6	0,8	8	7	4	10	8	4	12	5,5	7
3	20	0,6	0,4	0,8	10	6,5	3	8	6	8	6	6	8
4	25	0,4	1,2	1,4	12	5	4	10	4,5	7	8	7,5	5
5	30	1,2	0,8	1	14	4	3	15	5	6	10	6,5	6
6	20	1,4	0,6	1	10	3	6	8	5,5	4	12	6	4
7	25	1,6	0,4	0,8	12	2,5	4	10	6	5	14	7,5	5
8	15	0,8	1,2	0,6	6	8	8	12	7	7	10	8	6
9	10	0,6	1	0,4	8	6,5	2	12	8	6	10	7	7
10	20	1,2	1	1,2	10	6	3	6	7	4	8	4,5	8

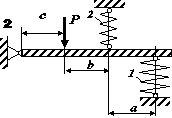
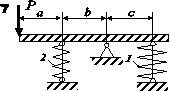
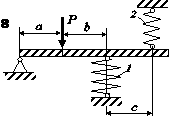
Рис. 2.4

План розв’язання задачі

1. Записати умови рівноваги.

2. Записати умову сумісності деформацій пружин.

3. Визначити опорні реакції.

4. Розрахувати напруження та деформації пружин..

Тема 3: «Плоский поперечний згин»

Задача 1. Визначення нормальних та дотичних напружень у балках-консолях

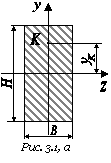
Для балки-консолі прямокутного поперечного перерізу (рис. 3.41, а), схема навантаження якої представлена на рис3.. 41, б, б, у небезпечному перерізі для точки К визначити дотичні та нормальні напруження. Розміри балки та значення навантаження вибрати з таблиці 43.1 згідно індивідуального варіанту студента.

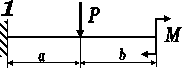
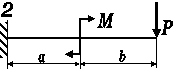
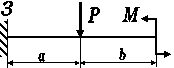
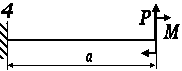
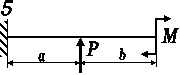
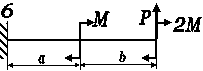
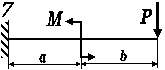
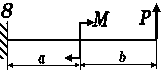
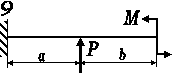
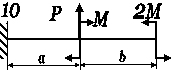Рис. 3.42, б

Таблиця 3.14

Схема	а, м	b, м	М, кН·м	P, кН	В, см	Н, см	уK, см
0	1	1	20	20	10	20	4
1	1,5	1	30	10	12	18	5
2	1	1,5	40	20	8	20	6
3	1,5	0,5	20	10	12	22	10
4	1,5	1,5	20	15	10	24	11
5	1	2,5	40	20	14	20	7
6	1,5	1,5	30	30	12	16	3
7	1,5	0,5	20	20	10	14	2
8	2	1	40	25	12	20	9
9	1	1,5	40	30	8	18	8

План розв’язання задачі

1. Поділити балку на ділянки, починаючи з вільного кінця (або з допомогою рівнянь рівноваги визначити опорні реакції у точці защемлення — тоді поділ на ділянки можна здійснювати довільним чином).

2. Побудувати епюри поперечних сил та згинальних моментів для балки-консолі.

3. Визначити небезпечний переріз (переріз (и), у яких згинальний момент досягає максимального значення). У небезпечному перерізі знайти значення згинального моменту М_* та поперечної сили Q_*.

4. Використовуючи форму формулу Нав’є:

,

визначити нормальні напруження. Тут J_z — момент інерції перерізу (у випадку прямокутника ), у_К — відстань від точки, у якій слід розрахувати напруження до нейтральної осі.

5. За допомогою формули Журавського:

,

розрахувати дотичні напруження у небезпечному перерізі. Тут S´ — статичний момент площі відсіченої частини перерізу, В — ширина перерізу.

Задача 2. Перевірка міцності за нормальними напруженнями простої балки

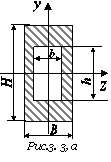Перевірити сталеву просту балку коробчастого поперечного перерізу (рис. 3.53, а), що навантажена згідно схеми (рис. 3.54, б), на міцність за нормальними напруженнями.

Розміри балки та значення навантаження вибрати з таблиці 3.25 згідно індивідуального варіанта студента.

При розрахунках враховувати, що . Значення допустимих напружень вибрати на основі додатку 1 для відповідної марки сталі.

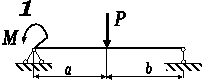
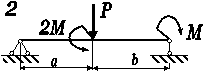
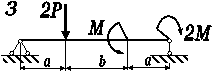
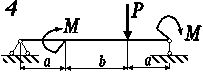
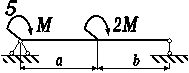
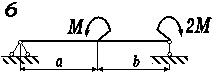
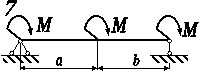
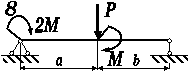
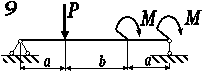
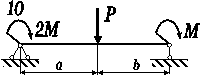
Рис. 3.54, б

Таблиця 3.25

Схема	а, м	с, м	М, кН·м	P, кН	В, см	Н, см	Матеріал
0	1	1	20	20	10	20	Сталь 10
1	1,2	1	25	10	12	18	Сталь 20
2	1,3	1,7	30	25	8	20	Сталь 25
3	1,4	0,7	35	15	12	22	Сталь 30
4	1,5	1,5	40	35	10	24	Сталь 35
5	1,6	2,4	45	40	14	20	Сталь 40
6	1,2	0,6	40	45	12	16	Сталь 45
7	1,6	0,8	35	50	10	14	Сталь 20Г
8	2	1	30	25	12	20	Сталь 50Г
9	1	1,2	35	30	8	18	Сталь 60

План розв’язання задачі

1. За допомогою рівнянь рівноваги визначити опорні реакції.

2. Поділити балку на ділянки, на кожній з яких визначити поперечну силу та згинальний момент.

3. Побудувати епюри поперечних сил та згинальних моментів для простої балки.

4. Визначити небезпечний переріз та значення максимального згинального моменту М_max.

5. Використовуючи умову міцності за нормальними напруженнями:

,

перевірити міцність балки. Тут W_z — момент опору перерізу; допустимі напруження визначаються: , де — напруження, що відповідають площинці текучості (вибирається на основі додатку 1), — коефіцієнт запасу (=1,5).

Задача 3. Повна перевірка на міцність консольної балки

Для двотаврової сталевої балки, номер профілю якої вказаний у таблиці 63.3, виконати повну перевірку міцності, застосувавши третю теорію міцності. Схема навантаження балки вказана на рис. 3.65.

З таблиці 6 3.3 для вказаного індивідуального варіанта студента підібрати розміри балки, матеріал, з якого вона виготовлена та значення навантаження.

Значення допустимих напружень вибрати на основі додатку 1 для відповідної марки сталі.

Таблиця 3.36

Схема	а, м	b, м	с, м	М, кН·м	P, кН	Двотавр	Матеріал
0	1	1,5	0,5	20	20	20	Сталь 10
1	1,2	1,4	0,4	25	10	20а	Сталь 20
2	1,3	0,7	1	30	25	22	Сталь 25
3	1,4	0,9	0,7	35	15	22а	Сталь 30
4	0,5	0,5	1	40	35	24	Сталь 35
5	1,6	1	0,4	45	40	24а	Сталь 40
6	1,2	0,6	1,2	40	45	27	Сталь 45
7	1,6	0,8	0,6	35	50	27а	Сталь 20Г
8	0,5	1	0,5	30	25	30	Сталь 50Г
9	0,8	0,8	0,4	35	30	30а	Сталь 60

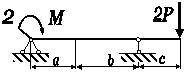
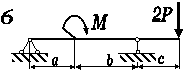
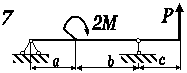
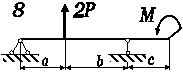
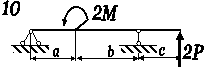
Рис. 3.56

План розв’язання задачі

1. За допомогою рівнянь рівноваги визначити опорні реакції.

2. Поділити балку на ділянки, на кожній з яких визначити значення поперечної сили та згинального момента.

3. Побудувати епюри поперечних сил та згинальних моментів для консольної балки.

4. Визначити небезпечний переріз.

5. Встановити значення максимального згинального моменту М_max та максимальної поперечної сили Q_max.

6. Використовуючи умову міцності за нормальними напруженнями:

,

перевірити міцність балки. Тут W_z — момент опору перерізу; допустимі напруження визначаються: , де —нормальні напруження, що відповідають площинці текучості (вибирається на основі додатку 1), — коефіцієнт запасу (=1,5).

7. Використовуючи умову міцності за дотичними напруженнями:

,

перевірити міцність балки. Тут J_z — момент інерції перерізу, S´_y — статичний момент півсічення, d — товщина стінки; допустимі дотичні напруження визначаються: , де τ_т — дотичні напруження, що відповідають площинці текучості (вибирається на основі додатку 1), — коефіцієнт запасу (=1,5).

8. Перевірити міцність балки за еквівалентними напруженнями. Для цього, у перерізі, де поперечна сила та згинальний момент досягають максимальних (достатньо великих) значень розрахувати головні:

та еквівалентні напруження:

.

Тут σ_*, τ_* — нормальні та дотичні напруження у перерізі, де згинальний момент та поперечна сила досягають максимальних (достатньо великих) значень.

Якщо , то результати повної перевірки міцності балки відповідатиме встановленим вимогам.

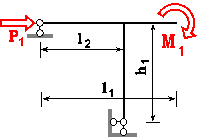
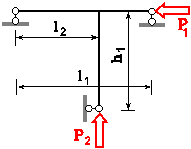
Задача 4. Розрахунок плоскої рами

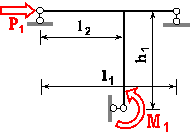
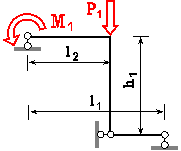
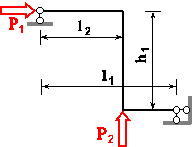
Для статично визначної рами, поданої на рис. 3.76, побудувати епюри внутрішніх силових факторів та підібрати прямокутний переріз з заданим відношенням розмірів для вказаної марки сталі.

З таблиці 73.4 для вказаного індивідуального варіанта студента підібрати розміри рами, матеріал, з якого вона виготовлена та значення навантаження.

Значення допустимих напружень вибрати на основі додатку 1 для відповідної марки сталі.

Таблиця 73.4

Схема	P1, кН	P2, кН	М1, кНм	h1, м	h2, м	l1, м	l2, м	h/b	Матеріал
0	15	25	20	1,0	0,6 h1	2,0	0,5 l1	2,0	Сталь 10
1	20	40	10	1,2	0,5 h1	2,2	0,4 l1	2,1	Сталь 20
2	55	15	40	1,4	0,4 h1	2,4	0,3 l1	2,2	Сталь 25
3	40	30	30	1,6	0,3 h1	2,6	0,4 l1	2,3	Сталь 30
4	35	25	45	1,8	0,4 h1	2,8	0,6 l1	2,4	Сталь 35
5	20	30	50	2,0	0,5 h1	3,0	0,7 l1	1,5	Сталь 40
6	-15	35	35	1,8	0,6 h1	2,8	0,5 l1	1,6	Сталь 45
7	-20	40	25	1,6	0,7 h1	2,6	0,3 l1	1,7	Сталь 20Г
8	-30	20	15	1,4	0,8 h1	2,4	0,4 l1	1,8	Сталь 50Г
9	-35	45	20	1,2	0,6 h1	2,0	0,6 l1	1,9	Сталь 60

1		2		3		4
5		6		7		8
9		10

Рис. 3.76

План розв’язання задачі

1. За допомогою рівнянь рівноваги визначити опорні реакції.

2. Поділити раму на ділянки, на кожній з яких визначити значення поздовжньої, поперечної сил та згинального моменту. Побудувати епюри внутрішніх силових факторів.

3. Визначити небезпечний переріз.

4. Встановити значення максимального згинального моменту М_max та максимальної поздовжньої та поперечної сил N_maх.та Q_max.

5. Використовуючи умову міцності за нормальними напруженнями:

,

підібрати розміри перерізу рами. Тут W_z — момент опору перерізу; допустимі напруження визначаються: , де —нормальні напруження, що відповідають площинці текучості (вибирається на основі додатку 1), — коефіцієнт запасу (=1,5).

6. Використовуючи умову міцності за дотичними напруженнями:

,

перевірити міцність рами. Тут J_z — момент інерції перерізу, S´_y — статичний момент півсічення, d — товщина стінки; допустимі дотичні напруження визначаються: , де τ_т — дотичні напруження, що відповідають площинці текучості (вибирається на основі додатку 1), — коефіцієнт запасу (=1,5).

7. Визначити максимальні значення нормальних напружень з врахуванням поздовжньої сили та перевірити міцність:

,

де М^*_max та N^*_maх відповідні значення силових факторів у перерізах рами.

Тема 4: «Розрахунок статично-невизначних систем»

Задача 1. Розрахунок статично невизначних балок

Для статично невизначної балки (рис. 4.1) побудувати епюри внутрішніх силових факторів та підібрати двотавровий переріз для вказаної марки сталі. Визначити переміщення у точці прикладання сили Р. При визначенні реакцій балки виконати деформаційну перевірку.

При розрахунках використати дані таблиці 1.

Таблиця 4.1.

№	М, кН м	P, кН	q, кН/ м	а, м	b, м	c, м	d, м	Матеріал
1	40	10	2	1	1,5	0,5	1	Сталь 10
2	25	12	1,6	1,2	1,4	0,4	1	Сталь 20
3	35	14	2,2	1,3	0,7	1	1,5	Сталь 25
4	45	15	0,4	1,4	0,9	0,7	0,5	Сталь 30
5	30	16	2,4	0,5	0,5	1	1,5	Сталь 35
6	20	19	1,2	1,6	1	0,4	2,5	Сталь 40
7	60	28	0,8	1,2	0,6	1,2	1,5	Сталь 45
8	55	17	1,8	1,6	0,8	0,6	0,5	Сталь 20Г
9	65	11	1,0	0,5	1	0,5	1	Сталь 50Г
10	50	13	0,6	0,8	0,8	0,4	1,5	Сталь 60

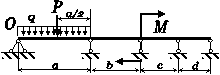
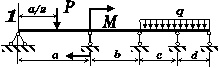
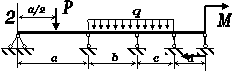
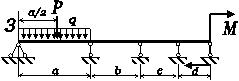
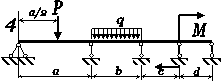
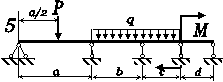
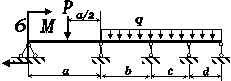
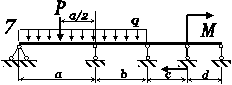
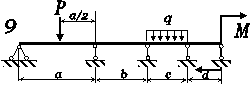
Рис. 4.1

План розв’язання задачі

1. Визначити міру статичної невизначеності балки.

2. Записати канонічні рівняння методу сил.

3. Визначити коефіцієнти та вільні члени канонічних рівнянь.

4. Розрахувати невідомі опорні реакції.

5. Побудувати епюру згинального моменту для балки.

6. З умови міцності визначити номер профілю двотаврого перерізу.

7. Визначити переміщення у точці прикладання сили Р.

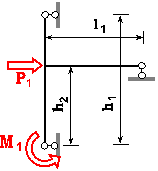
Задача 2. Проектний розрахунок рами

Для статично невизначної рами, що навантажена у своїй площині, побудувати епюри внутрішніх силових факторів та підібрати прямокутний переріз із заданим відношенням розмірів для вказаної марки сталі. При визначенні реакцій рами виконати деформаційну перевірку.

Таблиця 4.2

№	P, кН	q, кН/м	h1, м	h2, м	l1, м	l2, м	h/b	Матеріал
0	15	20	1,0	0,6 h1	2,0	0,5 l1	2,0	Сталь 10
1	20	10	1,2	0,5 h1	2,2	0,4 l1	2,1	Сталь 20
2	55	40	1,4	0,4 h1	2,4	0,3 l1	2,2	Сталь 25
3	40	30	1,6	0,3 h1	2,6	0,4 l1	2,3	Сталь 30
4	35	45	1,8	0,4 h1	2,8	0,6 l1	2,4	Сталь 35
5	20	50	2,0	0,5 h1	3,0	0,7 l1	1,5	Сталь 40
6	-15	35	1,8	0,6 h1	2,8	0,5 l1	1,6	Сталь 45
7	-20	25	1,6	0,7 h1	2,6	0,3 l1	1,7	Сталь 20Г
8	-30	15	1,4	0,8 h1	2,4	0,4 l1	1,8	Сталь 50Г
9	-35	20	1,2	0,6 h1	2,0	0,6 l1	1,9	Сталь 60

1		2		3		4			5		6
7		8		9		10

Рис. 4.2

План розв’язання задачі

1. Визначити міру статичної невизначеності рами.

2. Записати канонічні рівняння методу сил.

3. Визначити коефіцієнти та вільні члени канонічних рівнянь.

4. Розрахувати невідомі опорні реакції.

5. Побудувати епюри згинального моменту, поперечних та поздовжніх сил для рами.

6. З умови міцності визначити розміри поперчного перерізу рами.

Задача 3. Деформаційна перевірка рами

На рис. 4.3 зображена навантажена в своїй площині рама, вертикальні елементи якої мають моменти інерції J, а горизонтальні елементи ‑ k·J. Потрібно визначити переміщення шарнірно-рухомих опор.

Розрахункові дані узяти з таблиці 4.3.

Таблиця 4.3.

№	l, м	h, м	q, кН/м	k	J, см^4	№	l, м	h, м	q, кН/м	k	J, см^4
1	11	2	15	1,1	873	6	6	2	6	1,6	1150
2	12	3	20	1,2	1290	7	7	3	7	1,7	1200
3	3	4	30	1,3	350	8	8	4	8	1,8	1670
4	4	5	4	1,4	1430	9	9	5	9	1,9	960
5	5	6	5	1,5	1840	10	10	6	10	2,0	680

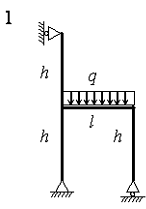
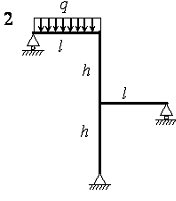
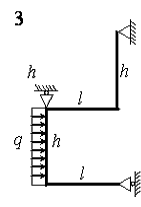
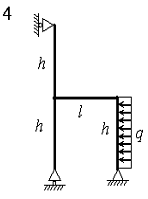
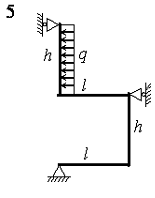
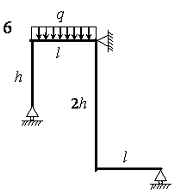
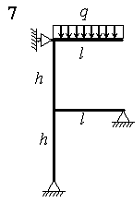
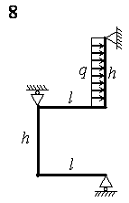
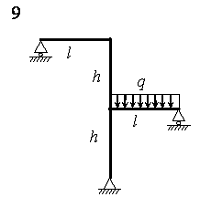
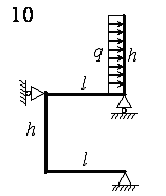Рис. 4.4.

План розв’язання задачі

1. Встановити ступінь статичної невизначеності і вибрати основну систему.

2. Написати канонічні рівняння.

3. Побудувати епюру М від одиничних сил і від заданого навантаження.

4. Знайти коефіцієнти канонічних рівнянь;

5. Знайти величини «зайвих невідомих» Х;

6. Виконати деформаційну перевірку правильності визначення невідомих;

7. Побудувати кінцеві епюри внутрішніх силових факторів N, Qy, Mx.

8. Визначити переміщення шарнірно-рухомих опор.

Тема 5: «Складний опір»

Задача 1. Неплоский (косий) згин

Схема а.

Для балки-консолі (рис. 5.1) підібрати прямокутний переріз при заданому відношенні висоти балки h до її ширини b, розмістивши сторони h та b паралельно до осей y та z найбільш раціонально.

Знайти положення нейтральної осі у небезпечному перерізі балки, побудувати просторову епюру нормальних напружень по перерізу. Визначити повний прогин вільного кінця консолі.

Розміри балки, матеріал, з якого вона виготовлена, значення навантаження вибрати з таблиці 5.1 згідно індивідуального варіанту студента.

При розрахунках допустимих напружень враховувати, що , де — напруження, що відповідають площинці текучості (вибирається на основі додатку 1 для вказаної у таблиці 5.1 марки сталі), — коефіцієнт запасу (=1,5).

Таблиця 5.1

№	q, кН/м	P, кН	М, кНм	l, м	a, м	c, м	φ, º	h/b	Матеріал
0	2	5	10	10	2	3	20	2,0	Сталь 10
1	4	10	20	8	1	2	25	2,1	Сталь 20
2	6	15	30	9	3	5	30	2,2	Сталь 25
3	8	10	40	12	4	4	25	2,3	Сталь 30
4	10	25	50	11	5	1	40	2,4	Сталь 35
5	12	30	-50	17	1	6	45	1,5	Сталь 40
6	14	-5	-40	16	6	7	50	1,6	Сталь 45
7	16	-10	-30	18	8	8	60	1,7	Сталь 20Г
8	18	-20	-20	16	2	3	65	1,8	Сталь 50Г
9	20	-30	-10	14	9	2	70	1,9	Сталь 60

3

4

5

6

9

10

8

7

2

1

10

9

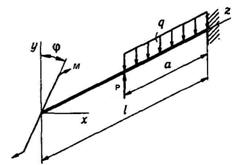
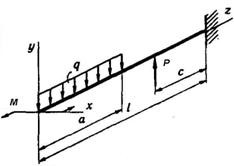
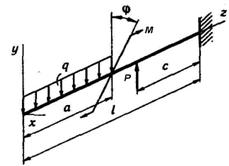
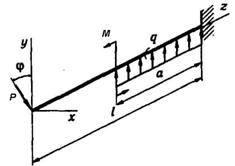
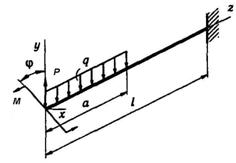
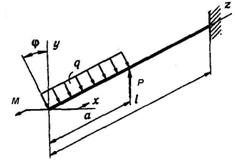
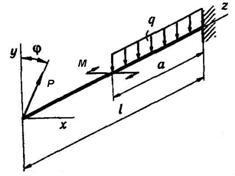
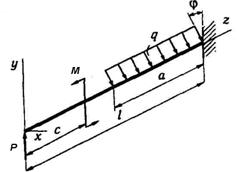
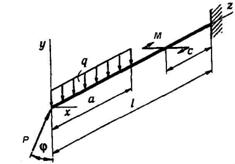
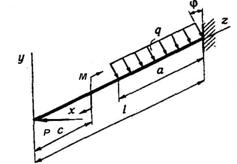
Рис. 5. 1

Схема б.

Для дерев’яної балки на шарнірних опорах, що навантажена згідно схеми, показаної на рис. 5.2, підібрати розміри прямокутного перерізу h та b (при заданому відношенні висоти балки до її ширини), розмістивши сторони паралельно до головних осей найбільш раціонально.

Побудувати просторову епюру нормальних напружень по перерізу. Визначити повне переміщення перерізу, позначеного точкою А на рис. 5.2.

При розрахунках допустимі напруження вибрати рівними 8 МПа. Розміри балки, значення навантаження вибрати з таблиці 5.2 згідно індивідуального варіанту студента.

Таблиця 5.2

Варіант	q, кН/м	P, кН	М, кНм	a, м	(, º	h/b
0	5	12	-12	2	30	2,0
1	6	-10	10	1	45	2,1
2	8	-8	-8	3	60	2,2
3	10	-6	6	4	120	2,3
4	12	-5	-5	5	135	2,4
5	-5	12	12	1	150	1,5
6	-6	1	-10	2	210	1,6
7	-8	8	8	3	225	1,7
8	-10	6	-6	2	240	1,8
9	-12	5	5	4	300	1,9

107

102

104

103

108

1010

106

105

109

10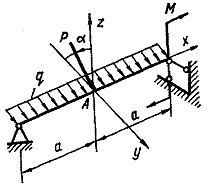

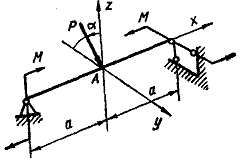
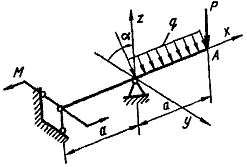
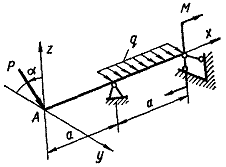
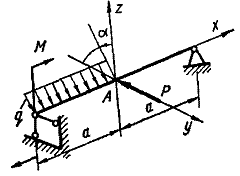
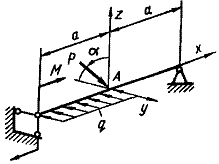
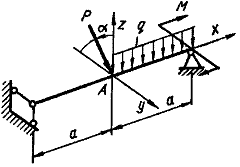
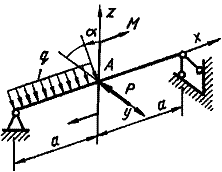
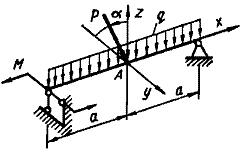
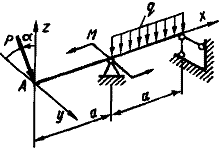
Рис. 5.2

План розв’язання задачі

1. Розкласти задані навантаження у головних центральних площинах yх та zх і побудувати епюри поперечних сил та згинальних моментів .

2. Визначити небезпечний переріз на основі аналізу епюр згинальних моментів: у небезпечному перерізі згинальні моменти набувають максимальних значень.

3. Встановити найбільш раціональне розміщення перерізу відносно навантаження. Якщо , то переріз слід розмістити таким чином, щоб .

4. Знайти розміри перерізу балки, виходячи з умови міцності:

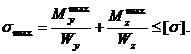
5. Визначити положення нейтральної осі у небезпечному перерізі балки, кутовий коефіцієнт якої розраховується:

.

6. Побудувати просторову епюру розподілу нормальних напружень по перерізу.

7. Визначити горизонтальний , вертикальний та повний прогин вільного кінця консолі.

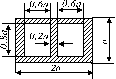
Задача 2. Позацентровий розтяг (стиск)

Схема а.

Чавунний короткий стрижень, поперечний переріз якого зображений на рис. 5.3, стискається силою Р, що прикладена в точці А. Потрібно:

1) обчислити найбільше стискаюче та найбільше розтягуюче напруження в поперечному перерізі, виразивши величини цих напружень через Р та розміри перерізу;

2) знайти допустиме навантаження Р при заданих розмірах перерізу для відповідної марки чавуну.

При розрахунках допустимих напружень враховувати, що , , де — напруження, що відповідають межі міцності (вибирається на основі додатку 2 для вказаної у таблиці 5.3 марки чавуну), nm — коефіцієнт запасу (nm =3).Розміри поперечного перерізу стрижня взяти з таблиці 3.

Таблиця 5.3.

№	а, см	b, см	Марка чавуну	№	а, см	b, см	Марка чавуну
1	6	4	СЧ 12	6	2	6	СЧ 28
2	2	3	СЧ 35	7	8	2	СЧ 35
3	3	5	СЧ15	8	3	6	СЧ 24
4	7	4	СЧ 38	9	4	8	СЧ 32
5	5	9	СЧ 18	10	5	6	СЧ 21

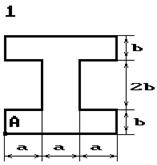
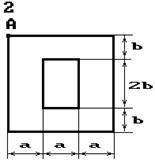
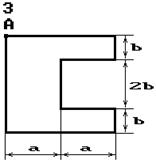
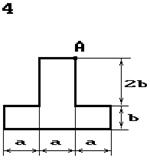
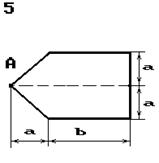
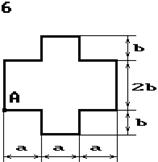
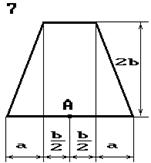
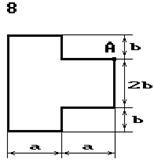
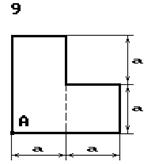
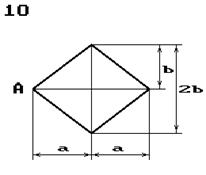
Рис. 5.3

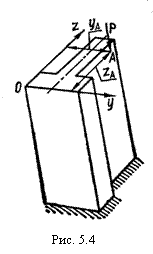
Схема б.

Для короткого стрижня, форма поперечного перерізу якого показана на рис. 5.5, визначити допустиме навантаження, якщо відомі координати y_A та z_A точки прикладання рівнодійної всіх навантажень Р (рис. 5.4) і величина допустимих напружень , , а також побудувати просторову епюру нормальних напружень по перерізу.

Необхідні для розрахунку дані використати з таблиці 5.4.

Таблиця 5.4.

№	, см	, см	а, см	№	, см	, см	а, см
1	10	20	50	6	10	30	50
2	30	40	60	7	30	40	60
3	30	60	70	8	40	30	70
4	40	25	80	9	20	40	80
5	35	40	90	10	40	50	100

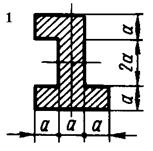
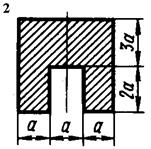
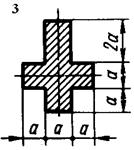
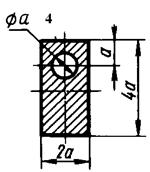
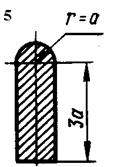
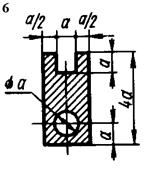
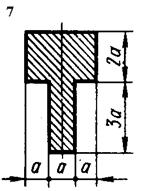
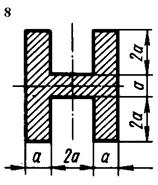
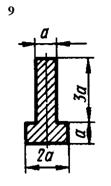
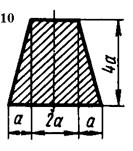Рис. 5.5

План розв’язання задачі

1. Визначити положення центру ваги перерізу.

2. Розрахувати осьові та відцентрові моменти інерції перерізу відносно центральних осей .

3. Визначити положення головних центральних осей інерції, враховуючи, що кут нахилу головних центральних осей відносно центральних знаходиться:

4. Розрахувати величину головних центральних моментів інерції:

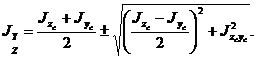
5. Визначити координати прикладання рівнодійної Р всіх навантажень відносно головних центральних осей інерції.

6. Знайти величину згинальних моментів відносно головних центральних моментів інерції.

7. Визначити допустиме навантаження з умови міцності в найбільш небезпечній точці перерізу:

,

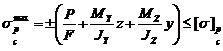де — координати точки, в якій визначаються напруження (у системі голових центральних осей), — площа поперечного перерізу.

8. Встановити положення нейтральної осі, рівняння якої задається:

,

де — радіуси інерції.

9. Побудувати в аксонометрії епюру розподілу напружень по перерізу.

Задача 3. Розрахунок вала на згин з крученням

Схема а.

На вал насаджені три зубчасті колеса, що навантажені силами Р1, Р2 та Р3, які прикладені до коліс з діаметрами D1, D2 та D3 відповідно, причому сила Р1 — вертикальна, а сили Р2 та Р3 — горизонтальні (рис. 5.6). Підібрати діаметр вала d з умови міцності на згин з крученням.

При розрахунках допустимих напружень враховувати, що , де — напруження, що відповідають площинці текучості (вибирається на основі додатку 1 для вказаної у таблиці 5.5 марки сталі), — коефіцієнт запасу (=1,5).

Розміри вала та діаметри зубчастих коліс взяти з таблиці 5 згідно індивідуального варіанту студента.

Таблиця 5.5.

№	Р1	Р2	Р3	a	b	c	D1	D2	D3	Матеріал вала
	кН	кН	кН	м	м	м	см	см	см
1	2	—	-4	1,1	0,9	1,3	10	12	16	Сталь 20
2	5	-2	—	1,2	0,8	0,4	20	24	28	Сталь 25
3	-3	4	—	1,3	0,7	1,5	24	26	14	Сталь 30
4	-4	—	2	1,4	0,6	1,6	36	30	26	Сталь 35
5	—	-3	4	1,5	0,5	0,7	16	24	12	Сталь 40
6	-5	—	1	1,6	0,4	1,8	30	28	16	Сталь 45
7	-6	-3	—	1,7	0,3	0,9	22	16	14	Сталь 50
8	5	—	-2	1,8	0,2	1,0	26	10	28	Сталь 10
9	—	2	-4	1,9	1,1	1,8	18	24	26	Сталь 20Г
10	—	3	5	1,0	1,0	1,2	32	30	10	Сталь 30Г

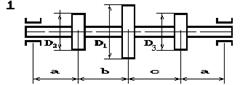
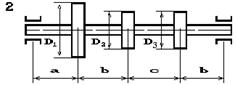
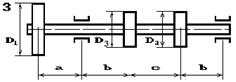
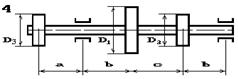
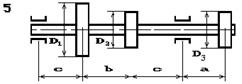
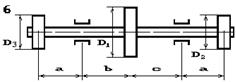
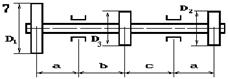
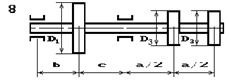
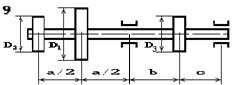
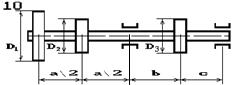
Рис. 5.6

План розв’язання задачі

1. Визначити моменти скручувальних пар сил, що створюються на кожному зубчастому колесі.

2. З умови рівноваги вала під дією системи скручувальних пар сил визначити значення сили , що не задана у таблиці 5.5.

3. Знайти крутні моменти Мкр та побудувати їх епюру.

4. Визначити згинальні моменти у горизонтальній (Мгор) та вертикальній (Мверт) площинах та побудувати їх епюри.

5. Побудувати епюру повного згинального моменту:

.

6. Визначити небезпечний переріз та величину максимального розрахункового моменту (за четвертою теорією міцності):

.

7. Підібрати діаметр вала d при заданих допустимих значеннях нормальних напружень :

.

Схема б.

Стальний вал трансмісії (рис. 5.7) робить n об/хв і передає через два ведених шківи потужності, що задані у таблиці 5.6; діаметри шківів D1 , D2 та D3 відповідно. Визначити діаметр вала з умови міцності на згин з крученням.

При розрахунках допустимих напружень враховувати, що , де — напруження, що відповідають площинці текучості (вибирається на основі додатку 1 для вказаної у таблиці 5.6 марки сталі), — коефіцієнт запасу (=1,5).

Необхідні для розв’язування дані вибрати з таблиці 5.6 та рис. 5.8 відповідно до індивідуального варіанту студента.

Таблиця 5.6

№	N1	N2	N3	a	α1	α2	n	D1	D2	D3	Матеріал вала
	кН	кН	кН	м	˚	˚	об/хв	см	см	см
1	—	10	20	1,0	270	60	1000	50	30	26	Сталь 20Х
2	10	—	20	0,8	240	180	100	70	40	36	Сталь 50ХН
3	10	20	—	1,1	210	90	300	40	20	10	Сталь 30ХГСА
4	—	30	40	1,4	180	30	300	60	48	28	Сталь 35ХМ
5	30	—	40	1,2	150	210	400	80	60	40	Сталь 40ХФА
6	30	40	—	0,6	120	0	500	64	46	32	Сталь 40ХН
7	—	50	60	1,0	90	240	600	40	30	20	Сталь 12ХН3А
8	50	—	60	1,2	60	270	700	50	40	20	Сталь 30ХН3А
9	50	60	—	0,8	30	300	800	56	40	30	Сталь 38ХМЮА
10	—	90	50	1,4	0	330	900	78	60	40	Сталь 40ХНМА

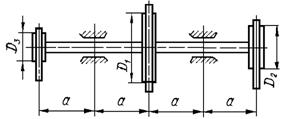
Рис. 5.7

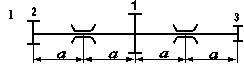
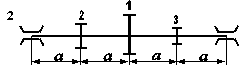
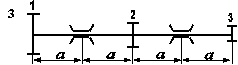
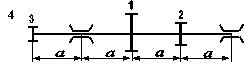
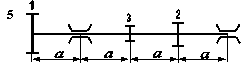
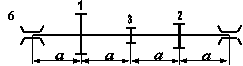
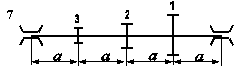
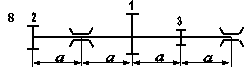
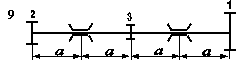
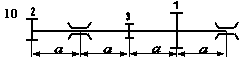
Рис. 5.8

План розв’язання задачі

1. З умови рівноваги вала визначити потужність на шківі, де вона не задана.

2. Знайти моменти скручувальних пар сил, що створюються на кожному шківі:

.

3. Визначити крутні моменти М_кр та побудувати їх епюру.

4. Визначити тиск, що передається шківами на вал, вважаючи, що натяг ведучої вітки паса в два рази більший, ніж натяг веденої:

, .

5. Показати на схемі в аксонометрії розміщення зусиль, що діють на вал і розкласти їх на горизонтальні та вертикальні складові.

6. Знайти величину складових , що діють у горизонтальній та вертикальній площинах.

7. Визначити згинальні моменти у горизонтальній (М_гор) та вертикальній (М_верт) площинах та побудувати їх епюри.

8. Побудувати епюру повного згинального моменту.

9. Визначити небезпечний переріз та величину максимального розрахункового моменту (за третьою теорією міцності):

.

10. Підібрати діаметр вала d при заданих допустимих значеннях нормальних напружень .

Схема в.

Стальний вал АВ (рис. 5.9) робить n об/хв і передає від ведучої через дві ведені шестерні потужності, задані у таблиці 5.6. Діаметри початкових обводів шестерень D₃, D₂, D₁ відповідно. Визначити діаметр вала, прийнявши, що .

План розв’язання задачі

Той самий, що і для схеми б за винятком пункту 4, який для схеми в запишеться:

4. Визначити тиск, що передається шестернями на вал, маючи на увазі, що між радіальною Р´ і коловою Р´´ складовими силами існує така залежність:

Вид за стрілкою К

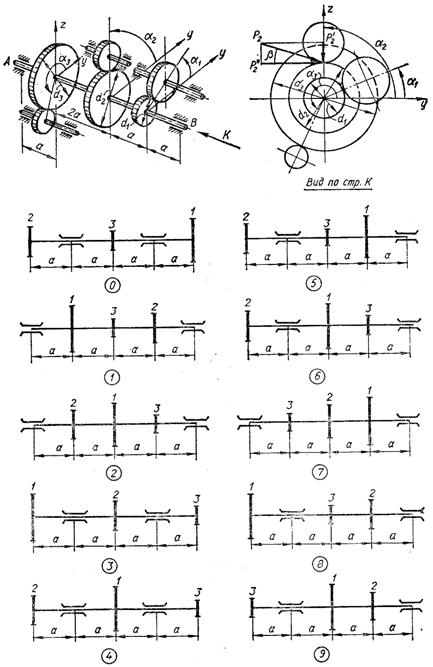
Рис. 5.9

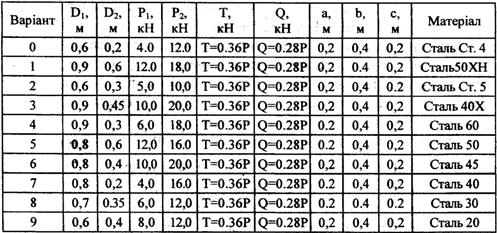
Схема г.

Вал круглого поперечного перерізу забезпечує передачу руху між встановленими на ньому циліндричними деталями, що мають діаметри D1 та D2. Деталі навантажені коловими силами Р1 та Р2, а також осьовою та радіальною силами Т та Q (рис. 5.9, а). З умови міцності вала на згин з крученням визначити необхідний діаметр вала та округлити його до найближчого більшого значення із стандартного ряду.

При розрахунках використайте дані таблиці 5.6, а

Таблиця 5.6, а

План розв’язання задачі

1. Визначити моменти скручувальних пар сил, що створюються на кожному зубчастому колесі.

2. Побудувати епюру крутного моменту М_кр.

3. Визначити згинальні моменти у горизонтальній (М_гор) та вертикальній (М_верт) площинах та побудувати їх епюри. Побудувати епюру повного згинального моменту.

4. Визначити небезпечний переріз та величину максимального розрахункового моменту.

5. Підібрати діаметр вала d при заданих допустимих значеннях нормальних напружень :

.

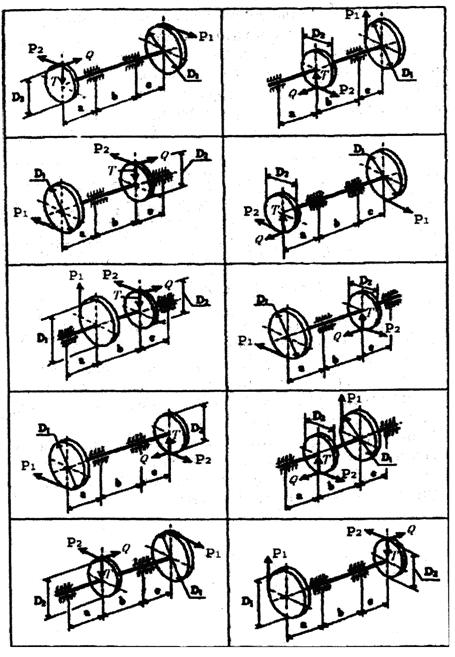
Рис. 5.9, а

Задача 4. Розрахунок на міцність бруса з ламаною віссю

Схема а.

На рис. 5.10 показана в аксонометрії вісь ламаного стрижня круглого поперечного перерізу, яка розміщена у горизонтальній площині (у точках А і В прямі кути). На стрижень діє вертикальне навантаження.

Визначити у небезпечному перерізі розрахунковий момент за четвертою теорією міцності та підібрати розміри поперечного перерізу, враховуючи, що [σ]=160 МПа.

При розрахунках використати дані з таблиці 5.7.

Таблиця 5.7.

№	α	q, кН/м	L, м	l, м	№	α	q, кН/м	L, м	l, м
1	1,1	10	1,2	1,4	6	1,3	20	2,3	1,9
2	0,4	20	1,5	2,5	7	1,5	18	1,6	2,4
3	0,9	12	2,6	1,3	8	0,6	22	2,2	1,8
4	1,4	16	1,1	1,8	9	1,2	10	1,7	2,1
5	0,8	10	1,4	2,4	10	0,7	14	2,4	2,0

Схема б.

Стальний ламаний плоскопаралельний брус (рис. 5.11) навантажений зосередженими силами Р1 та Р2. Підібрати розміри його поперечного перерізу, якщо напруження, що відповідають площинці текучості σm=420 МПа, а коефіцієнт запасу міцності — nm=3.

При розрахунках використати дані з таблиці 5.8.

Таблиця 5.8.

№	Р1, кН	Р2, кН	а1, м	а2, м	h/b	№	Р1, кН	Р2, кН	а1, м	а2, м	h/b
1	2	1	1,1	1,6	2	6	1	6	1,7	1,4	2
2	9	7	1,8	2,0	3	7	7	5	2,0	1,5	1,5
3	4	3	1,2	1,7	1,5	8	2	8	1,5	1,1	3
4	5	8	1,9	1,6	2	9	9	4	1,6	1,3	2
5	2	4	1,3	1,8	2,5	10	3	5	1,4	1,2	1

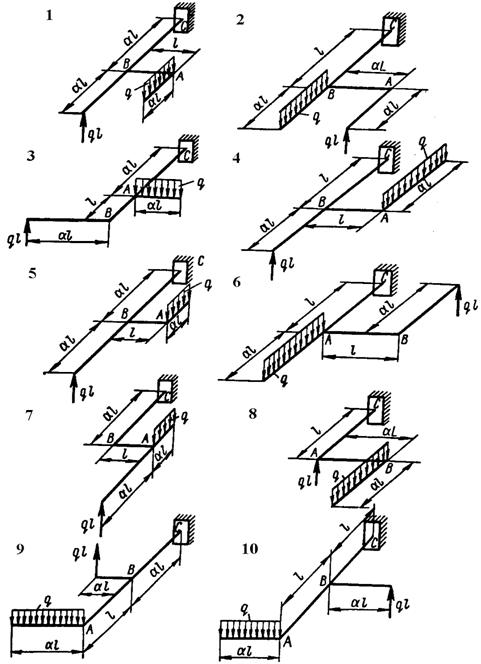
Рис. 5.10

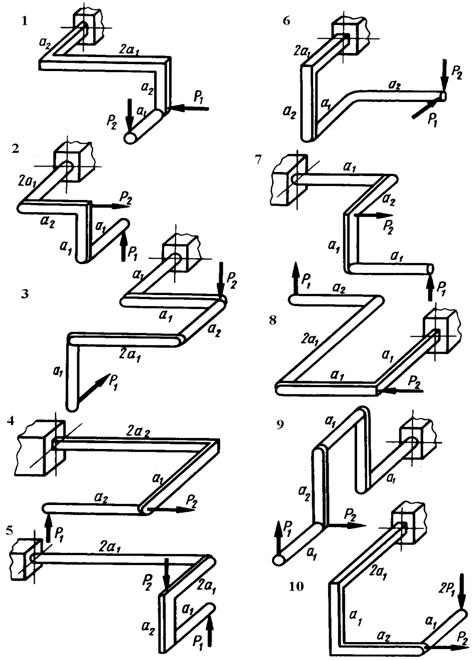
Рис. 5.11

План розв’язання задачі

1. Побудувати епюри згинальних та крутних моментів.

2. Побудувати епюри нормальних напружень згину і дотичних напружень кручення у небезпечному перерізі.

3. Користуючись критерієм найбільших дотичних напружень (третя теорія міцності) або енергетичним критерієм зміни форми (четверта теорія міцності) визначити розрахунковий момент.

4. Підібрати діаметр вала (схема а, б) та визначити розміри прямокутного поперечного перерізу (схема б).

Тема 6: «Розрахунок на стійкість»

Задача 1. Визначення критичної сили

Сталевий стрижень завдовжки l стискається силою Р (рис. 6.1). Потрібно знайти:

1) розміри поперечного перерізу при допустимих напруженнях на стиск [σ]=160 МПа (розрахунок проводити послідовними наближеннями, для початкового наближення вважати j=0,5);

2) величину критичної сили і коефіцієнт запасу стійкості.

Дані узяти з табл. 6.1.

Таблиця 6.1.

Варіант	Р, кН	l, м	Схема закріплення стрижня	Форма перерізу стрижня
1 2	100 200	2,1 2,2		I	II
3 4	300 400	2,3 2,4		III	IV
5 6	500 600	2,5 2,6		V	VI
7 8	700 800	2,7 2,8		VII	VIII
9 10	900 1000	2,9 3,0		IX	X

План розв’язання задачі

1. Записати умову стійкості. Визначити розміри перерізу стрижня.

2. Розрахувати гнучкість стрижня. Визначити відповідне значення коефіцієнта j.

3. Шляхом ітерації визначити розміри перерізу.

4. Визначити критичну силу.

5. Розрахувати дійсне, критичне напруження та коефіцієнт запасу стійкості.

Тема 7: «Динамічні задачі»

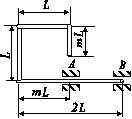
Задача 1. Розрахунок стрижневої системи з урахуванням сил інерції

Для заданої сталевої стрижневої системи, що складається зі сталевого вала АВ діаметром D i жорстко закріпленого з ним ламаного стрижня такого ж діаметра, що обертається зі сталою кутовою швидкістю ( (рис. 7.1), визначити з умови міцності граничну кутову швидкість обертання. При розрахунках використати дані таблиці 7.1.

Таблиця 7.1.

Значення	Варіант
	1	2	3	4	5	6	7	8	9	0
D, см	2	2,2	2,4	2,6	2,8	3	3,2	3,4	3,6	3,8
k	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
m	1	0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1
L, м	0,4	0,5	0,6	0,55	0,45	0,35	0,3	0,7	0,65	0,75
Марка сталі	20Г	45Х	40ХФА	50ХН	30Г	40Х	12ХНЗА	30ХМ	50Г	20Х

1				2
3				4
5				6
7					8
9			10

Рис.7. 1

План розв’язання задачі

1. Визначити сили інерції на ділянках стрижня.

2. З умови рівноваги визначити опорні реакції.

3. Побудувати епюру згинального моменту.

4. З умови міцності визначити граничну кутову швидкість обертання.

Задача 2. Розрахунок рами на удар

Для заданої сталевої рами двотаврового перерізу сталої жорсткості (рис. 7.2) визначити значення нормальних напружень, що виникають при ударі вантажу Q, що падає з висоти H, а також величину повного переміщення точки А рами. При розрахунках використати дані таблиці 7.2.

Таблиця 7.2.

Значення	Варіант
	1	2	3	4	5	6	7	8	9	0
Q, Н	100	80	90	110	120	50	60	70	130	140
H, м	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
m	0,1	0,6	0,4	0,5	0,2	0,5	0,4	0,3	0,2	0,1
L, м	1,4	1,5	0,6	0,8	0,9	1,1	1,3	1,7	1,6	1,2
L1/L	0,2	0,4	0,6	0,8	0,5	0,3	0,7	0,9	1,1	1,2
L2/L	0,9	0,8	0,3	0,5	1	0,7	1,4	1,1	0,7	0,6
№ профілю	10	12	14	16	12	14	16	12	10	14
Марка сталі	20Г	45Х	40ХФА	50ХН	30Г	40Х	12ХНЗА	30ХМ	50Г	20Х

1		2
3		4
5		6
7		8
9		10

Рис. 7.2

План розв’язання задачі

1. З умови рівноваги визначити опорні реакції.

2. Побудувати епюру згинального моменту при статичному прикладанні сили .

3. Визначити переміщення точки падіння вантажу.

4. Розрахувати коефіцієнт динамічності.

5. Визначити напруження при ударі.

6. Розрахувати динамічне переміщення точки А.