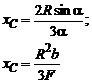Лабораторні роботи

 

 

 


Вступ

Прикладна механіка є складовою частиною нормативно-методичного забезпечення навчального процесу для підготовки бакалаврів напрямку 6.051003 “Приладобудування” галузі знань 0510 „Метрологія, вимірювальна техніка та інформаційно-вимірювальні технології” денної форми навчання.

Прикладна механіка включає в себе такі дисципліни як теорія механізмів і машин, опір матеріалів та деталі машин. Ця дисципліна ґрунтується на теоретичних розрахунках та експериментальних дослідженнях.

Тому складовою частиною прикладної механіки є лабораторні роботи, що сприяють розвитку навичок самостійної роботи та глибокому розкриттю фізичної суті теорії. Вони спрямовані на вивчення механічних властивостей різних матеріалів та експериментальну перевірку теоретичних висновків та формул.

Лабораторні роботи з прикладної механіки можна розділити на дві основні групи:

• визначення механічних характеристик матеріалів;

• визначення деформацій найпростіших елементів конструкцій та деталей машин.

Кожна лабораторна робота містить короткі теоретичні відомості, порядок проведення досліду, обробку його результатів та контрольні запитання. Послідовність виконання лабораторних робіт визначається згідно з робочою програмою дисципліни «Прикладна механіка».

Лабораторні роботи виконуються студентами в лабораторіях кафедри в присутності викладача та лаборанта. Перед виконанням роботи студенти повинні засвоїти відповідний розділ теоретичного курсу та ознайомитись з інструкцією до її виконання.

Лабораторна робота вважається виконаною після її захисту і підпису звіту викладачем. Захист проводиться у формі усної співбесіди з викладачем. Звіти з лабораторних робіт зберігаються у студента до закінчення семестру і надаються ним на заліках або іспитах. При виконанні лабораторних робіт необхідно чітко дотримуватись основних правил техніки безпеки:

1) в аудиторіях і лабораторіях кафедри забороняється знаходитись у верхньому одязі та вішати його на лабораторне устаткування чи класти на столи;

2) перед початком робіт студенти повинні ознайомитись з правилами техніки безпеки та розписатись в журналі інструктажу;

3) категорично забороняється чіпати, вмикати та вимикати випробувальні машини та інші прилади і обладнання без дозволу викладача чи лаборанта;

4) забороняється виконувати роботу без дозволу викладача, лаборанта;

5) забороняється переставляти вантажі, прилади, наочні посібники та інше;

6) необхідно пам’ятати, що необережне поводження з вогнем або паління в заборонених місцях може бути причиною вибуху або пожежі;

7) забороняється без дозволу вмикати та експлуатувати електронагрівачі (каміни, плитки та ін.);

8) при проведенні лабораторних робіт на випробувальних машинах необхідно упевнитись, що робочий простір машини має захисне та запобіжне устаткування;

9) при проведенні лабораторних робіт з використанням вимірюваної техніки студентам забороняється використовувана обладнання не за призначенням (інакше, ніж описано в інструкції до лабораторних робіт);

10) студентам забороняється виносити обладнання, устаткування (його частини) з лабораторії;

11) при виявлені несправностей обладнання та порушення правил техніки безпеки студенти повинні негайно інформувати викладача або лаборанта;

12) студенти, які порушили правила техніки безпеки, від роботи відстороняються, і про це інформувати завідувача кафедри та декана факультету;

13) після закінчення роботи студенти зобов’язані привести своє робоче місце у належний вигляд;

14) після проведення досліджень та приведення робочого місця до належного стану студент зобов’язаний передати устаткування і обладнання викладачу чи лаборанту.

Лабораторна робота №1

Тема: Випробування на розтяг зразка із маловуглецевої сталі

Мета роботи: вивчення поведінки маловуглецевої сталі в процесі розтягу до розриву.

Хід роботи

1. Теоретичні відомості

Випробування на розтяг є одним з найбільш поширених видів випробування матеріалів. Дані, отримані при розтягуванні зразка, дозволяють в багатьох випадках робити висновок про поведінку матеріалу при інших видах деформацій. Випробування на розтяг проводиться методом статичного навантаження, коли навантаження на зразок зростає постійно і безперервно, без поштовхів і ударів. Випробування виконується на розривних машинах із записуючим пристроєм, який малює графік залежності між навантаженням і абсолютною деформацією зразка в процесі навантажування, тобто діаграму розтягу. Для цієї мети може бути використана машина типу МИ-40КУ, яка працює в поєднанні з ЕОМ.

Форма і розміри зразка значно впливають на значення механічних характеристик. Для того, щоб результати дослідів зразків у різних матеріалів були порівняні, їх форма, розміри і умови навантажування визначаються стандартом ДСТУ 1497-61.

В лабораторній практиці застосовуються зразки круглого або прямокутного перерізу штангоподібної форми (з головками на кінцях) для закріплення їх у машині (рис. 1).

 

Рис. 1. Зразок до навантаження

Стандартний зразок називається основним при d0=10мм і l0=100мм. Згідно із ДСТУ використовуються і пропорційні зразки:

· довгі з відношення l0/d0=10;

· короткі з відношенням l0/d0=5.

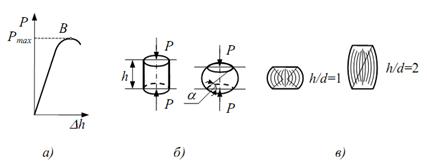
Однією з загальних задач дослідження на розтяг є отримання графіка залежності між силою P, що діє на зразок і його подовженням Δl. Цей графік, який називається діаграмою навантажень – викреслюється автоматично за допомогою програмного забезпечення випробовувальної машини МИ-40КУ. На рис. 2 показано діаграму розтягу зразка із маловуглецевої сталі.

На відрізку ОА, тобто початковій стадії навантажування, виявляється лінійна залежність між видовженням і силою розтягу; матеріал підлягає закону Гука. Деформації матеріалу в цій стадії пружні, і повністю зникають після зняття навантаження.

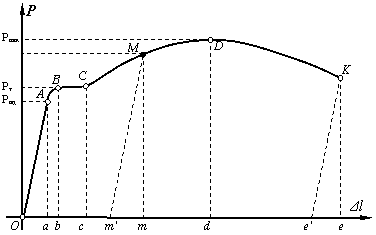
Рис. 2. Діаграма розтягу зразка

Ордината А являє собою силу Рпц, яка відповідає границі пропорційності. Це найбільше навантаження, при якому ще зберігається прямо пропорційна залежність між силою і деформацією.

При подальшому збільшенні навантаження лінійна залежність між силою і видовженням зразка порушується. Деформації зростають значно швидше від навантаження. Закон Гука втрачає свою силу. Одночасно з пружними з’являються пластичні деформації. Навантаження, при якому величина пластичних деформацій досягає 0.003%, називається навантаженням пружності Рпр,

При досягненні деякої величини, яка відповідає точці В, навантаження практично перестає зростати. Видовження зразка від точки В до С відбувається без помітного збільшення навантаження. Ділянка ВС називається зоною загальної текучості. Цю ділянку також часто називають площинкою текучості. Високовуглецеві сталі (як і інші матеріали, крім м'якої сталі) не мають площинки текучості. В межах ділянки ВС відбувається пластична (непружна) деформація матеріалу. Ордината В являє собою силу, яка відповідає величині Рт.

При появі пластичних деформацій полірована поверхня зразка мутніє внаслідок появи на ній тонких ліній або смуг ковзання, які називаються лініями Чернова-Людерса. Вони направлені до осі стержня під кутом 450 і практично співпадають з площинами максимальних дотичних напружень.

Після стадії текучості матеріал знову починає чинити опір зростаючому навантаженню, настає стадія зміцнення (ділянка СD). Тут видовження зразка супроводжується збільшенням навантаження, але більш повільно, ніж в пружній стадії. Після досягненні максимального навантаження (точка D), рівномірний по довжині розтяг зразка супроводжується рівномірним його звужуванням.

Ордината точки D являє собою найбільшу величину розтягуючої сили Pmax.

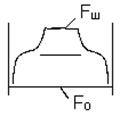
При максимальному навантаженні в зразку починає утворюватись місцеве звуження поперечного перерізу – шийка (рис. 3), внаслідок чого опір зразка навантаженню швидко зменшується, крива іде вниз.

Рис. 3. Утворення шийки на зразку

Відрізок Ое на осі абсцис являє собою зображення в масштабі повного видовження зразка в момент перед розривом. Відрізок Ое' – пластична (залишкова) деформація, відрізок е­е' – пружна (зникаюча) деформація зразка.

Площа діаграми, поміщена між кривою ОАВСDKе з віссю абсцис, являє собою роботу, затрачену на розрив зразка.

Якщо навантажити зразок до точки М, а потім поступово зняти це навантаження, то розвантаження пройде по прямій Mm¢, паралельній ОА. Відрізок mm¢ – пружна деформація, відрізок Om¢ – пластична. При повторному навантаженні цього зразка діаграма буде мати вигляд тієї ж прямої m¢M, а після точки М – вигляд кривої МDK. Границя пропорційності піднімається до тих навантажень, до яких попередньо був навантажений зразок і зменшує залишкове видовження. Це явище називається наклепом.

2. Порядок проведення досліду

1.    Перед дослідженням необхідно ознайомитись із будовою машини, на якій проводиться дослідження.

2.    Виміряти розміри зразка: діаметр, розрахункову та робочу довжини.

3.    Визначити площу поперечного перерізу F0. Результати замірів і підрахунків занести в табл.1.

Таблиця 1

Розміри зразка, мм

до досліду

після розриву

L0, мм

d0, мм

F0., мм2

l1, мм

d1, мм

F1, мм2

 

 

 

 

 

 

Характеристики міцності

навантаження, кН

деформації, мм

Рпц

Рт

Рmax

пружна

пластична

повна

 

 

 

 

 

 

4.    Ввімкнути машину, закріпити зразок в затискачах машини, ввести вихідні дані, дотримуючись послідовності, вказаної в додатку 1. Для розтягу необхідно вибрати відповідний режим роботи машини.

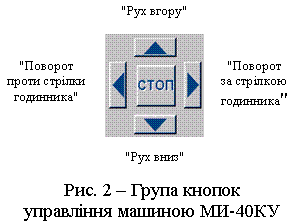
5.    Розпочати дослід, натиснувши кнопку "Рух вверх" (див. додаток 2). Швидкість випробування повинна бути незначною для уникнення неінерційних явищ (рекомендоване значення: 2..5мм/хв). На початку навантаження спостереження за поведінкою зразка ведеться за діаграмою, яка відтворюється на екрані монітора. Невелика початкова ділянка діаграми є, як правило, криволінійною. Це викликано відсутністю повного контакту між головками зразка і захватами машини.

6.    Під час досліду необхідно звернути увагу на:

·  стадію текучості матеріалу, при якому навантаження на деякий час перестає зростати, або швидкість зростання різко знижується;

· стадію утворення шийки. Як тільки навантаження досягне свого максимального значення, то під час подальшого розтягу на зразку з’явиться шийка. В шийці і в зоні, безпосередньо близької до неї, деформації зростають інтенсивніше, ніж на віддалених від неї відрізках зразка. При цьому навантаження падає і при деякому його значенні виникає розрив зразка.

3. Обробка результатів досліду

Встановивши характер руйнування зразка (дві його частини скласти разом, акуратно притиснувши один до другого) виміряти довжину l1, його розрахункової частини після розриву і діаметр шийки d1. Відрахування за шкалою штангенциркуля необхідно проводити, не знімаючи його із зразка. Довжину l1 можна визначити за допомогою діаграми. Для цього необхідно нанести на діаграму точку е', провівши лінію, паралельну ОА з точки K (точка розриву) до перетину з нульовою лінією навантажень. Тоді l1=l+Oe¢. Далі необхідно визначити площу поперечного перерізу зразка в місці розриву F1. Дані вимірювань та обчислень занести в табл. 1.

По отриманій діаграмі визначити наступні величини Рпц, Рт, Рmax, значення пружної, пластичної та повної деформації зразка. Обчислені дані занести в табл. 1.

4. Контрольні запитання

1.       Сформулюйте мету роботи.

2.       Які взірці застосовуються під час виконання цієї роботи?

3.       На якій машині виконана робота?

4.       Для якої ділянки діаграми розтягу справедливий закон Гука?

5.       Чим характеризується площинка текучості?

6.       Що відбувається у зоні зміцнення?

7.       За рахунок чого відбувається руйнування зразка після утворення шийки?

8.       В яких координатах будуються діаграма розтягу і діаграма навантажень?

9.       Що називається повною (абсолютною) повздовжньою деформацією і відносною поздовжньою деформацією? Яка розмірність абсолютної і відносної повздовжньої деформації?

10.   Яке явище називається наклепом?

11.   Що таке лінії Чернова-Людерса?

Лабораторна робота №2

Тема: Дослідження механічних характеристик маловуглецевої сталі

Мета роботи: побудова діаграми напружень для маловуглецевої сталі та визначення її механічних характеристик.

Хід роботи

1. Теоретичні відомості

На основі випробування на розтяг зразків проводиться визначення основних механічних характеристик матеріалу, які поділяють на характеристики міцності, характеристики пластичності та характеристики пружності.

Визначення характеристик міцності

Оскільки форма і розміри зразка значно впливають на значення механічних характеристик, то для отримання результатів, незалежних від розмірів, будується діаграма напружень: по осі ординат відкладається напруження , а по осі абсцис – відносне видовження  (рис. 1).

На відрізку ОА виявляється лінійна залежність між видовженням і силою розтягу; матеріал підлягає закону Гука.

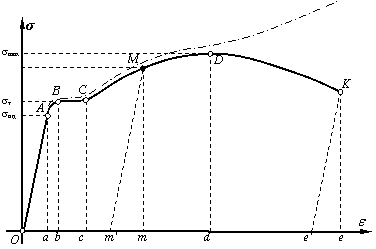
Рис. 1. Діаграма напружень

Ордината А являє собою границю пропорційності. Це найбільше напруження, при якому ще зберігається прямо пропорційна залежність між навантаженнями і деформаціями. Границя пропорційності визначається:

,       (1)

де F0 – площа поперечного перерізу навантаженого зразка.

Зона, де величина пластичних деформацій досягає 0,003%, називається границею пружності:

 .                                                                                                                                     (2)

Ділянка ВС, що є зоною загальної текучості, характеризується пластичною (непружною) деформацією матеріалу при постійній розтягу вальній силі. Напруження на цій ділянці називається границею текучості:

.                                                                                                                                         (3)

Для високовуглецевих і легованих сталей границя текучості приймається умовно відповідною напруженню, при якому залишкове подовження зразка складає 0,2% його довжини; позначаються σ0,2.

Зона зміцнення характеризується зростанням опору навантаженню. Умовне напруження, яке відповідає найбільшій величині розтягуючої сили Pmax називається тимчасовим опором або границею міцності (витривалості):

.                                                                                                                              (4)

При максимальному навантаженні в зразку починає утворюватись шийка, внаслідок чого опір зразка навантаженню швидко зменшується, крива іде вниз. Проте істинне напруження в шийці зростає і досягає максимального значення до моменту розриву (в 2–3 рази перевищує границю міцності σт.о).

На рис. 1 суцільною лінією показано умовну діаграму (що побудована при умові сталої площі поперечного перерізу). Проте при видовженні зразка спостерігається зменшення площі поперечного перерізу. Тому дійсні напруження у зоні пластичних деформацій дещо вищі умовних, а особливо вони зростають після утворення шийки на зразку. Тому дійсна діаграма позначена на рис. 1 штрихпунктирною лінією.

 

Визначення характеристик пластичності

Величина залишкової деформації зразка характеризує пластичність матеріалу. Мірою пластичності матеріалу є відносне залишкове видовження при розриві:

,                                                                                                                      (5)

і відносне звуження в шийці:

 ,                                                                                                                           (6)

де l0 – довжина робочої частини зразка до його навантаження; l1 – довжина робочої частини зразка після його розриву; F1 – площа поперечного перерізу зразка в самому вузькому місці шийки після його розриву (рис. 2).

Рис. 2 Визначення площі шийки зразка

Для конструкційних сталей ; .

Матеріали, для яких , вважають крихкими, а для яких – пластичними.

Пластичні матеріали руйнуються після великих пластичних деформацій. У крихких пластичні деформації при руйнуванні незначно перевищують пружні деформації.

 

2. Обробка результатів досліду

1.    Використати дані, отримані в результаті проведення досліджень у лабораторній роботі № 1.

2.    Визначити характеристики міцності маловуглецевої сталі за формулами (1), (3), (4) обчислити характеристики міцності.

3.    За формулами (5), (6) визначити характеристики пластичності матеріалу. Обчислені дані занести в табл. 1.

 

 

Таблиця 1

Характеристики міцності

Характеристики пластичності

напруження, МПа

σпц

σт

σв

d3

y

 

 

 

 

 

4. Контрольні запитання

1.     Сформулюйте мету роботи.

2.     Які параметри характеризують міцність матеріалу?

3.     Які параметри характеризують пластичність матеріалу?

4.     Що називається границею міцності, границею текучості і границею пропорційності?

5.     В яких координатах будуються діаграма напружень?

6.     Як за результатами досліду визначити марку сталі?

Лабораторна робота №3

Тема: Визначення модуля пружності сталі

Мета роботи: перевірка закону Гука і визначення дослідним шляхом модуля поздовжньої пружності Е (модуля Юнга) сталі.

Хід роботи

1. Теоретичні відомості

У лабораторній роботі № 2 було зазначено, що розрізняють механічні характеристики міцності, пластичності та пружності. Для визначення останніх слід проводити дослідження у зоні пружних деформацій, тобто навантаження, що прикладатиметься до зразка, має не перевищувати межу пропорційності матеріалу.

В початковий період навантаження для більшості металів справедливий закон Гука, тобто його абсолютна деформація лінійно залежить від навантаження, що діє на елемент конструкції або зразок:

.                                                                                                                                      (1)

На підтвердження справедливості закону Гука для сталі будують діаграму розтягу (рис. 1) тільки до площинки текучості в координатах «навантаження – абсолютне видовження». Отримана діаграма являє собою прямолінійну ділянку. Це дозволяє визначити модуль пружності Е з формули, яка виражає закон Гука:

.                                                                                                                                      (2)

Оскільки , то , тобто для визначення Е потрібно виміряти деформацію зразка Δl і силу P.

Модуль Юнга (модуль пружності першого роду) – постійна для даного матеріалу величина, яка характеризує пружну властивості матеріалу, його здатність чинити опір зміні форми і розмірів та має розмірність напруження.

Геометричний зміст модуля пружності першого роду полягає в тому, що він являє собою тангенс кута нахилу до осі абсцис прямолінійної ділянки діаграми напружень. Оскільки абсолютне видовження прямо пропорційне відносному видовженню Δl=l0×e, а сила P прямо пропорційна напруженню P=F×σ, то від діаграми Р—Δl (рис. 1) легко перейти до діаграми напружень σ—e (рис. 2), яка відрізнятиметься лише масштабами абсциси та ординати. З цієї діаграми видно, що відношення  на прямолінійній ділянці діаграми і дорівнює:

.                                                                                                                                        (3)

Також для кожної точки, яка лежить на цій прямій, справедливий вираз:

.                                                                                                                                     (4)

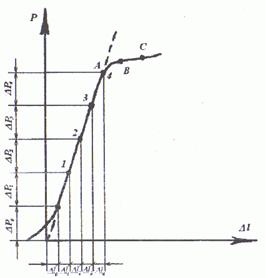
Рис. 1. Діаграма розтягу

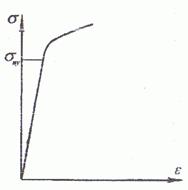
Рис. 2. Діаграма напружень

Таким чином, отримаємо:

.                                                                                                                                         (5)

Модуль Юнга являється основною характеристикою пружності і широко використовується в розрахунках. Значення Е під час розтягу і стиску для одного і того ж матеріалу дещо відрізняється, але ця різниця невелика, тому прийнято вважати модуль пружності однаковим як при розтягу, так і при стиску.

На величину модуля Юнга впливають температура, напруження і ступінь неоднорідності матеріалу. Так, при підвищенні температури модуль Е зменшується. При великих напруженнях модуль пружності менший, ніж при малих напруженнях. Обробка металів тиском підвищує стабільність цієї характеристики.

2. Підготовка досліду

Для проведення досліду необхідні:

1.    Зразок: являє собою плоску сталеву штабу прямокутного поперечного перерізу.

2.    Прилади: для вимірювання деформацій необхідні два важільні тензометри (рис. 3), які прикріплюються до зразка за допомогою струбцинок (рис. 4) з двох протилежних сторін. Парне розташування тензометрів виключає вплив нерівномірності розтягу штаби. Для розрахунків приймається середня величина деформації зразка, яка дорівнює півсумі двох осесиметричних волокон. (Необхідно мати на увазі, що тензометри вимірюють деформацію зразка в межах бази приладу).

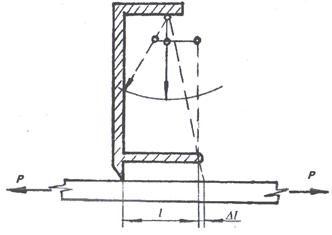
Рис. 3. Схема важільного тензометра

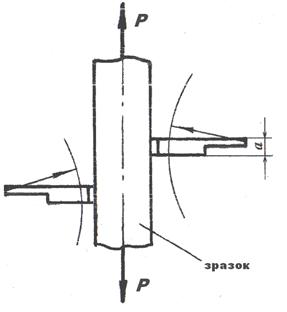
Рис. 4. Розміщення тензометрів

3.    Випробна машина: для виконання роботи використо­вується розривна машина.

 

3. Проведення досліду

1. До початку досліду проводять заміри робочої частини смуги: ширини b та товщини h. Враховуючи складність встановлення зразка і тензометрів, цю роботу виконують завчасно.

2. Приступаючи до навантаження, необхідно визначити величину максимальної сили, яку можна прикладати до зразка, не викликаючи в ньому напружень, більших від границі пропорційності:

,                                                                                                                                     (6)

для маловуглецевої сталі прийняти σпц = 200 МПа=2000 кг/см2.

3. Спочатку прикласти до зразка попереднє навантаження, яке приймається за умовний нуль. При цьому зафіксувати перші покази приладів. Надалі плавне навантаження зразка вести ступенями з постійним приростом ΔР. Для кожного ступеня навантаження збільшувати до виникнення у взірці напружень, які становлять 65–80% значення границі пропорційності. При цьому звернути увагу на те, що однаковим приростам навантажень повинні відповідати однакові прирости деформацій згідно закону Гука.

4. Для ілюстрації справедливості закону Гука в межах прикладеного навантаження і одержаних деформацій слід побудувати діаграму процесу деформацій в координатних осях. Графік побудований по точках на основі дослідних даних повинен виражатись прямою лінією.

5. Внаслідок можливих похибок під час фіксації показів тензометрів не виключені незначні відхилення від строгої лінійної залежності між деформаціями і навантаженнями. Тому слід побудувати графік, що відповідатиме теоретичному процесу деформуванню. Для цього необхідно визначити жорсткість стрижня за формулою:

 ,                                                                                                                                     (7)

де Ет — теоретичне значення модуля Юнга для маловуглецевої сталі (Ет=2∙106 кг/см2), F — площа поперечного зразка, l — довжина досліджуваного зразка (при розрахунках приймається довжині базі приладу). Потім слід визначити деформації, що відповідають навантаженню, для якого проводилися експериментальні дослідження, на основі закону Гука:

.                                                                                                                                         (8)

 Отримані результати слід нанести на графік, що відповідає експериментальним дослідженням та зробити відповідні висновки.

6. Підрахувати для кожного тензометра окремо всі прирости деформацій, які викликані приростами навантажень; визначити середнє значення величини деформації зразка:

,        (9)

де ΔSпр – сума приростів деформацій за показами правого тензометра; ΔSлів – сума приростів деформації за показами лівого тензометра; n – кількість зафіксованих приростів деформацій (4–5).

Приріст напруження, викликаний приростом навантаження:

.                                                                                                                                       (10)

Середній приріст відносного подовження

,                                                                                                                                  (11)

де        а – база тензометра;

           k – коефіціент збільшення важільного тензометра.

Таким чином, формула (3) набирає вигляду:

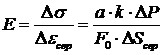.                                                                                                                   (12)

4. Оформлення звіту

Звіт про лабораторну роботу включає:

1.     Назву і мету роботи.

2.     Схему тензометра та схему установки тензометрів.

3.     Визначення максимального навантаження Pmax.

4.     Попередні дані:

a.                             матеріал зразка;

b.                             розміри зразка b і h;

c.                              площа поперечного перерізу F0;

d.                             початкове навантаження P0;

e.                              база приладу, а = 10см;

f.                               коефіцієнт збільшення приладу k = 1000.

5.     Визначити жорсткість стрижня за формулою (7).

6.     Результати дослідів та теоретичних розрахунків на основі формули (8) занести до таблиці 1.

7.     Побудувати графіки залежностей деформацій від навантаження, прикладеного до зразка, отримані експериментально та теоретично.

8.     Зробити висновки про виконання закону Гука для зразка.

9.     Середнє значення величини деформації обчислити за формулою (9).

10.                Значення модуля пружності Е визначити за формулою (12).

11.                Порівняти теоретичне і дослідне значення модуля пружності Е.

12.                Зробити висновки та визначити похибку.

 

 

 

Таблиця 1.

№

Наван­тажен­ня,

Р (Н)

Приріст наванта­ження ΔР, (Н)

Покази тензометрів,

мкм

Середнє значення показів тензомет­рів, мкм

Теоре­ти­чні зна­че­ння де­формацій, мкм

Приріст показів тензометрів, мкм

правого, Sпр

лівого, Sлів

правого, ΔSпр

лівого, ΔSлів

1

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

4. Контрольні запитання

1.     Сформулюйте мету роботи.

2.     Якими приладами визначаються деформації при дослідженнях?

3.     Що таке база приладу?

4.     Сформулюйте закон Гука.

5.     Що таке модуль Юнга?

6.     Чому при проведенні досліду використовуються два прилади?

7.     Як графічно реалізується закон Гука?

8.     В яких координатах будуються діаграма розтягу?

Лабораторна робота №4

Тема: Визначення коефіцієнту Пуассону сталі

Мета роботи: визначення дослідним шляхом коефіцієнта Пуассона μ сталі.

Хід роботи

1. Теоретичні відомості

Відомо, що при одновісному розтязі зразок деформується як в поздовжньому так і поперечному напрямку. Досліди показують, що для переважної більшості матеріалів поперечна деформація в 3−4 рази менша, ніж поздовжня.

Численні експерименти показують, що поздовжня і поперечна деформація у тілі мають протилежні знаки. Якщо розглянути розтяг зразка (рис. 1) та позначити через Δl - абсолютне видовження стрижня, то відносна поздовжня деформація визначатиметься:

.

Відносне звуження або відносна поперечна деформація знаходитиметься:

Абсолютне значення відношення поперечної відносної деформації ε' до відносної поздовжньої деформації ε називається коефіцієнтом Пуассона або коефіцієнтом поперечної деформації і позначається зазвичай буквою µ

µ=|ε'/ε|.                                                                                                                                         (1)

Коефіцієнт Пуассона — це міра зміни поперечних розмірів ізотропного тіла при деформації розтягу. Його ще називають коефіцієнтом поперечної деформації.

Для різних матеріалів µ змінюється в межах 0…0,5. Для абсолютно крихкого матеріалу коефіцієнт Пуассона дорівнює 0, для абсолютно пружного — 0,5. Для більшості металів µ=0,3, для гуми він приблизно дорівнює 0,49. Для сталі він змінюється в межах 0,25…0,3.

Коефіцієнт Пуассона може бути також від’ємним. Це значить, що при розтязі поперечні розміри тіла збільшуються. Такі матеріали називаються ауксетіками (в основному це полімери).

Величина коефіцієнта Пуассона при розтязі і стиску однакова, тобто знак зусилля на значення µ не впливає. Для ізотропних матеріалів E і µ, як фізичні константи матеріалів, повністю характеризують їх пружні властивості.

Значення коефіцієнтів Пуассона для різних матеріалів наведено в таблиці 1.

 

Таблиця 1.

Матеріал

Коефіцієнт Пуассона, μ

Чавун сірий, білий

Сталі вуглецеві

Сталі леговані

Мідь прокатна

Бронза фосфориста катана

Бронза марганцевиста катана

Латунь холоднотягнута

Латунь катана

Алюміній канатний

Цинк катаний

Свинець

Скло

Каучук

Бетон: класу В20

 класу В15

 класу В10

0,23-0,27

0,24-0,28

0,25-0,30

0,31-0,34

0,32-0,35

0,35

0,32-0,42

0,36

0,32-0,36

0,27

0,42

0,25

0,47

0,16-0,18

0,16-0,18

0,16-0,18

 

2. Підготовка досліду

Для проведення досліду необхідні:

1.          Зразок: являє собою плоску сталеву штабу прямокутного поперечного перерізу.

2.          Прилади: для вимірювання деформацій необхідні два важільні тензометри (рис. 2), які прикріплюються до зразка за допомогою струбцинок з однієї сторони, причому один із тензометрів слід розмістити вертикально, а інший — горизонтально (рис.3). Для розрахунків приймаються величини поздовжньої та поперечної деформацій зразка. (Необхідно мати на увазі, що тензометри вимірюють деформацію зразка в межах бази приладу).

Рис. 2. Схема важільного тензометра

Рис. 4. Розміщення тензометрів

3.          Випробна машина: для виконання роботи використо­вується розривна машина.

3. Проведення досліду

1. До початку досліду проводять заміри баз тензометрів, що розміщені вертикально і горизонтально. Враховуючи складність встановлення зразка і тензометрів, цю роботу виконують завчасно.

2. Приступаючи до навантаження, необхідно визначити величину максимальної сили, яку можна прикладати до зразка, не викликаючи в ньому напружень, більших від границі пропорційності:

,        (6)

для маловуглецевої сталі прийняти σпц = 200 МПа=2000 кг/см2.

3. Спочатку прикласти до зразка попереднє навантаження, яке приймається за умовний нуль. При цьому зафіксувати перші покази приладів. Надалі плавне навантаження зразка вести ступенями з постійним приростом ΔР. Для кожного ступеня навантаження збільшувати до виникнення у взірці напружень, які становлять 65–80% значення границі пропорційності. При цьому звернути увагу на те, що однаковим приростам навантажень повинні відповідати однакові прирости деформацій згідно закону Гука.

4. Підрахувати для кожного тензометра окремо всі прирости деформацій, які викликані приростами навантажень; визначити середнє значення величини деформації зразка:

, ,                                                                                                           (2)

де ΔSвер – сума приростів деформацій за показами вертикально розміщеного тензометра; ΔSгор – сума приростів деформації за показами горизонтально розміщеного тензометра; n – кількість зафіксованих приростів деформацій (4–5).

5. Середній приріст відносного подовження визначається:

,                                                                                                                                     (3)

Середній приріст відносного звуження становить:

,                                                                                                                                    (4)

де а – база вертикального тензометра; b – база горизон­тального тензометра;      k – коефіцієнт збільшення важільного тензометра.

Таким чином, формула (1) набирає вигляду:

.                                                                                                                                       (5)

4. Оформлення звіту

Звіт про лабораторну роботу включає:

13.                Назву і мету роботи.

14.                Схему тензометра та схему установки тензометрів.

15.                Визначення максимального навантаження Pmax.

16.                Попередні дані:

a.   матеріал зразка;

b.  початкове навантаження P0;

c.   база вертикального та горизонтального приладу: а = 10см, b = 4см;

d.  коефіцієнт збільшення приладу k = 1000.

17.                Результати дослідів занести до таблиці 2.

18.                Середнє значення величини деформацій обчислити за формулою (2).

19.                Приріст відносного подовження та відносного видовження визначити за формулами (3) та (4).

20.                Визначити експериментальне значення коефіцієнта Пуассона за формулою (5)

21.                Порівняти теоретичне (визначене з таблиці 1) і дослідне значення коефіцієнта Пуассона μ

22.                Зробити висновки та визначити похибку

Таблиця 2.

№

Наванта­ження, Р (кг)

Приріст наванта­ження ΔР, (кг)

Покази тензометрів,

мкм

Приріст показів тензометрів, мкм

вертикаль­ного Sвер

горизонталь­ного, Sгор

вертикаль­ного Sвер

горизон­та­льного, Sгор

1

 

 

 

 

 

 

2

 

 

 

 

 

 

3

 

 

 

 

 

 

4

 

 

 

 

 

 

5

 

 

 

 

 

 

4. Контрольні запитання

1.     Сформулюйте мету роботи.

2.     Якими приладами визначаються деформації при дослідженнях?

3.     Що таке коефіцієнт Пуассона?

4.     Яке значення коефіцієнту Пуассона для різних матеріалів?


Лабораторна робота №5

Випробування взірців на стиск

 

Мета роботи: вивчення поведінки матеріалів під час статичного стиску та визначення їх механічних характеристик.

Хід роботи

1.     Теоретичні відомості

При стиску пластичні та крихкі матеріали ведуть себе по різному.

Пластичні матеріали (маловуглецеві сталі, алюміній, мідь та ін.) однаково добре працюють як на розтяг, так і на стиск, тому випробування на стиск являється доповненням до випробування цих матеріалів на розтяг. В процесі випробування таких матеріалів обмежуються спостереженнями за їх поведінкою і характером деформацій.

Крихкі матеріали (чавун, бетон, цемент камінь і ін.) на розтяг працюють значно гірше, тому вони застосовуються тільки в елементах конструкцій, що працюють на стиск (колони, дамби, фундаменти і ін.). Основним видом випробувань крихких матеріалів являється випробування на стиск.

Випробування на стиск на відміну від випробувань на розтяг мають свої особливості:

1.        В процесі випробування пластичні матеріали можуть стискатись, не руйнуючись при цьому і не розкришуючись, а крихкі — руйнуються;

2.       Характеристики міцності та деформацій циліндричного зразка під час випробувань на стиск суттєво залежать від відношення висоти зразка до його діаметра;

3.       На результати випробувань значно впливають сили тертя, що виникають між торцями зразка і опорними плитами машини.

Силу тертя можна зменшити змащуванням торців зразка графітом чи графітовою змазкою; при цьому величина границі міцності буде дещо нижчою.

Для випробувань на стиск будуть використовуватись взірці із різних матеріалів.

Металеві взірці виготовлені у вигляді циліндриків висотою h = 10мм і діаметром d = 5мм, при цьому повинно зберігатись співвідношення:. Дерев’яні зразки мають фору кубика зі стороною а = 10см.

Випробування сталі

При стиску зразка до деякого значення навантаження спостерігається пропорційна залежність між деформацією і навантаженням, яке викликає цю деформацію (рис. 1, а). Відношення Рпц до початкової площі поперечного перерізу називається границею пропорційності сталі при стиску:

.                                                                                                                                      (1)

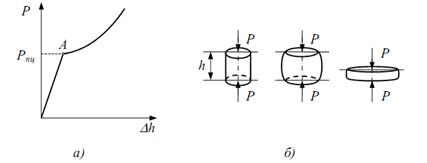
Рис.1. Деформування сталі шляхом стиску

При подальшому навантаженні спостерігається значне зростання деформацій, тобто матеріал "тече", але без чітко вираженої площинки текучості. Зразок набирає діжкоподібної форми (рис. 1, б) внаслідок того, що сили тертя між торцями зразка і опорними плитами машини гальмують розвиток деформацій біля торців зразка.

Для збільшення деформацій необхідно різко збільшити стискуюче навантаження. Зразок розплющується, часом виникають тріщини по краях. Пластичні матеріали при стиску не мають границі міцності, тобто їх можна розплющувати до отримання фольги (рис. 1, б).

Випробування чавуну

При стисканні чавунного зразка з самого початку навантаження і до руйнування спостерігається нелінійна залежність між зусиллям і переміщенням. Але в умовах тих малих деформацій, при яких матеріал використовують в різних деталях машин і споруд, діаграма P~∆h являє собою лінію малої кривизни (рис. 2, а). Тому при практичних розрахунках вважають, що матеріал деформується, дотримуючись закону Гука. При поступовому навантаженні зразок коротшає, приймаючи діжкоподібну форму (рис. 2, б), а при досягненні максимального зусилля Pmax руйнується з утворенням магістральної тріщини (рис. 2, в). Руйнування відбувається при невеликих пластичних деформаціях від максимальних дотичних напружень, які діють на площинах, нахилених до осі зразка приблизно під кутом 40°...50°

Рис. 2. Деформування чавуну шляхом стиску

Відношення зусилля Pmax до площі F0 поперечного перерізу називається границею міцності або тимчасовим опором чавуну при стиску:

.                                                                                                                                      (2)

При досягненні максимального зусилля Pmax чавун руйнується практично миттєво, що характерно для крихких матеріалів. Необхідно пам’ятати, що границя міцності чавуну сильно залежить від умов випробування і відношення висоти h до діаметра d зразка, від якого залежить навіть вид руйнування крихких матеріалів (рис. 2, в).

Випробування деревини

Випробування дерев’яного зразка як представника анізотропних матеріалів проводиться вздовж (рис. 3, б) і поперек (рис. 3, в) волокон.

Діаграма P~∆a при стисканні зразка вздовж волокон (рис. 3, а, крива 1) зовні схожа на діаграму стискання чавуну (крихкого матеріалу). Між зусиллям Р і переміщенням ∆a на початку навантаження помітна незначна нелінійна залежність, причому ця нелінійність зростає по мірі збільшення зусилля. При досягненні максимального зусилля Pmax зразок руйнується.

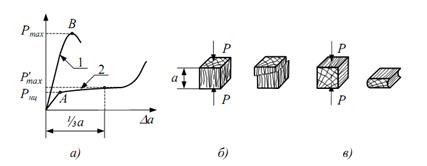
Рис.3. Деформування деревини

Відношення Pmax до початкової площі F0 поперечного перерізу зразка називається границею міцності або тимчасовим опором дерева вздовж волокон і визначається формулою:

.                                                                                                                                      (3)

Зазвичай руйнування відбувається з утворенням поперечних складок і зминанням торців. При стисканні зразка впоперек волокон діаграма P~∆a має інший вигляд (рис. 3, а, крива 2) і нагадує діаграму стискання сталевого зразка (пластичного матеріалу). До деякої точки А спостерігається пропорційна залежність між зусиллям Pпц і переміщенням, що дозволяє визначити границю пропорційності як відношення Pпц до початкової площі F0 поперечного перерізу, яке визначається формулою:

.                                                                                                                                      (4)

При подальшому навантаженні деревина здатна дуже сильно ущільнюватись без помітних ознак руйнування зразка. Момент втрати несучої здатності зафіксувати неможливо. Тому за руйнуючу силу P′max умовно приймають таке зусилля, при дії якого деформація (ущільнення) зразка досягне ⅓ початкового значення, тобто ∆a=⅓a.

Відношення P′max до F0 називається границею міцності або тимчасовим опором дерева при стисканні поперек волокон:

 .                                                                                                                                    (5)

Порівнюючи криві 1 і 2 (рис. 3, а) можна помітити, що при стиску до руйнування поздовж волокон зразок зазнає значно менші деформації, ніж при стисканні поперек волокон. Характер руйнування у двох випадках різний. Міцність зразка в першому випадку у 7…10 разів більша, ніж у другому.

Коефіцієнт анізотропії, який характеризує відмінність механічних властивостей дерева вздовж і поперек волокон, визначається як відношення границі міцності при стисканні вздовж волокон до границі міцності при стиску поперек волокон:

.                                                                                                                                         (6)

2. Порядок проведення досліду

1.    Перед дослідженням необхідно ознайомитись із будовою машини, на якій проводиться дослідження.

2.    Виміряти розміри зразків: діаметри та довжину (для сталевих та чавунних зразків) та довжину грані (для дерев’яного).

3.    Визначити площу поперечного перерізу А0. Результати замірів і підрахунків занести в табл.1.

4.    Ввімкнути машину, встановити по черзі зразки на нижню робочу плиту машини, ввести вихідні дані, дотримуючись послідовності, вказаної в додатку 1. Для стиску необхідно вибрати відповідний режим роботи машини. Регулятор граничного значення осьового зусилля виставити в максимальне положення.

5.    Розпочати дослід, натиснувши кнопку "Рух вниз" (див. додаток 2). Швидкість випробування повинна бути незначною для уникнення неінерційних явищ (рекомендоване значення: 2..5мм/хв).

6.    Під час досліду необхідно звернути увагу на зміну форми зразка під час деформування.

7.    Після досягнення граничного значення осьового зусилля рух рухомої частини автоматично зупиниться. Натиснувши кнопку "Рух вгору" підняти рухому плиту, звільнити здеформовані зразки.

3. Обробка результатів досліду

1. Встановити характер руйнування. За отриманою діаграмою визначити Рпц, Рmax, Р¢max та за формулами (1) – (4) обчислити характеристики міцності. Обчислені дані занести в табл.1.

Таблиця 1

Випробування сталі

Розміри зразка

Навантаження
пропорційності

Границя пропорційності

l0

d0

F0

Pпц

σпц

 

 

 

 

 

Випробування чавуну

Розміри зразка

Навантаження міцності

Границя міцності

l0

d0

F0

Pmax

 

 

 

 

 

Випробування деревини (вздовж волокон)

Розміри зразка

Навантаження міцності

Границя міцності

а

F0

Pmax

 

 

 

 

Випробування деревини (впоперек волокон)

Розміри зразка

Навантаження пропорційності

Границя пропорційності

Руйнуюча сила

Границя міцності

а

F0

Pпц

σмц

P¢max

 

 

 

 

 

 

4. Контрольні запитання

1.  Сформулюйте мету роботи.

2.  Які взірці застосовуються під час виконання цієї роботи?

3.  На якій машині виконана робота?

4.  Чим пояснюється діжкоподібна форма деформованого при стиску сталевого зразка?

5.  Які механічні характеристики можна визначити при стиску м’якої сталі?

6.  Яким чином руйнується чавунний зразок при стиску?

7.  Як руйнується деревина при стиску вздовж волокон?

8.  Що відбувається при стиску деревини впоперек волокон?

9.  Що таке коефіцієнт анізотропії деревини?

Лабораторна робота №6

Визначення положення центру ваги перерізу

 

Мета роботи: встановити положення центру ваги плоского перерізу та перевірити отримане значення експериментально.

Хід роботи

1. Теоретичні відомості

Одним з важливих елементів інженерних розрахунків є визначення положення центру ваги перерізу тіла. При відомому положенню центру ваги можна робити висновки про вид деформацій, які виникають у тілі під дією заданого навантаження (простий напружений стан: розтяг-стиск, зсув, кручення чи згин або складний: сумісна дія декількох видів простих напружених станів).

Центр паралельних сил

Поняття центру ваги пов’язують з центром паралельних сил (рис. 1). Центром паралельних сил називається точка на лінії дії рівнодійної цих сил, яка не змінює свого положення при повороті всіх сил навколо точок їх прикладання на один і той же кут в одному напрямку.

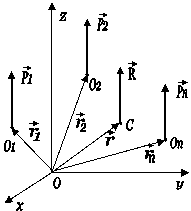
Рис.1. Система паралельних сил

Віднесемо систему паралельних сил  до декарто­вої системи координат. Позначимо через  радіус-вектори точок прикладання сил. Рівнодійна цієї системи прикладена в точці С, радіус-вектор якої визначається:

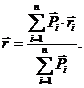                                                                                                                                    (1)

Спроектувавши векторну рівність (1) у декартову систему координат отримаємо три еквівалентні рівності:

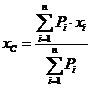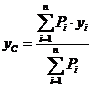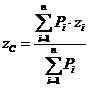, , ,                                                                                         (2)

тут Рі — модулі сил системи, взяті з відповідним знаком, (хі; yi; zi) — координати прикладання точок сил. 

З формул (1) та (2) випливає, що положення центру паралельних сил не залежить від напрямку дії сил, а залежить  від точок їх прикладання, модулів сил та знаків величин Рі. Звідси випливає властивість системи паралельних сил: якщо всі сили заданої системи паралельних сил повернути на один і той же кут, зберігаючи незмінними їх точки прикладання, то і рівнодійна цих сил повернеться на такий же кут, причому положення центру паралельних сил не зміниться.

Величини , ,  називаються статичними моментами системи паралельних сил відносно координатних площин. Якщо початок координат розмістити у точці С, статичні моменти будуть рівні нулю.

Центр ваги

Нехай маємо тверде тіло, що знаходиться поблизу поверхні Землі. На кожну елементарну частинку цього тіла діють сили притягання до Землі, напрямлені по вертикалі вниз — ваги цих частинок (рис. 2).

Сили  притягаються під кутами, що є досить малими, тому можна вважати, що ці сили паралельні. Центр С цієї системи паралельних сил називається центром ваги даного тіла, а рівнодійна цих сил

,

що проходить через точку С, є вагою даного тіла. Якщо тіло віднести до декартової системи координат, то координати точки С(хС; yC; zC) визначаються за формулою (2).

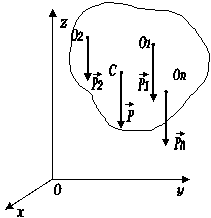
Рис.2. Центр ваги тіла

Якщо позначити вагу одиниці об’єму тіла через γ, то формули (2) запишуться у вигляді:

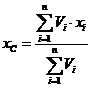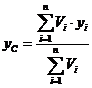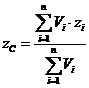, , ,                                                                                         (3)

де Vi — об’єми елементарних частин, на які розбивається тіло.

Якщо розглянути однорідну оболонку та позначити вагу одиниці її площі через γ, то формули (2) запишуться у вигляді:

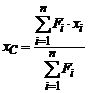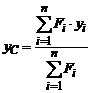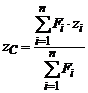, ,                                                                                            (4)

де Fi — площі елементарних частин, на які розбивається оболонка.

Для випадку однорідної пластинки формули (4) перепишуться у вигляді:

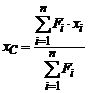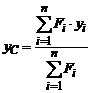 , .                                                                                                             (4¢)

Для випадку однорідного стрижня, якщо позначити вагу одиниці довжини через γ, формули (2) матимуть вигляд вигляді:

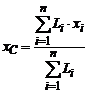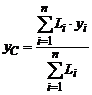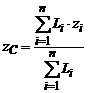, ,                                                                                            (5)

де Li — довжини елементарних частин, на які розбивається стрижень.

У формулах (3), (4), (4¢) та (5) під елементарними частинами розуміють такі частини розглядуваного тіла, оболонки (пластинки) чи стрижня, для яких відоме положення їх центру ваги та об’єму, площі чи довжини.

Для випадку, коли розглядуване тіло утворюється шляхом відтинання (вирізання) елементарних частин (має отвори, порожнини чи вирізи), то положення центру ваги визначається за правилом від’ємних об’ємів (площ):

 для перерізу, що має отвори, порожнини чи вирізи положення центру ваги можна визначити на основі формул (3), (4), (4¢) вважаючи, що порожнини, отвори чи вирізи мають від’ємний об’єм чи площу.

Якщо розглядуване тіло має площину, вісь чи центр симетрії то положення центру ваги визначається за правилом симетрії:

 для перерізу, що має площину, вісь чи центр симетрії, положення центру ваги лежить у площині, на осі чи співпадає з центром симетрії.

Відмітимо, що при визначенні положення центру ваги тіла, оболонки (пластинки) чи стрижня поділ на елементарні частини здійснюється на основі принципу раціональності обчислень, 

 

 

Центри ваги та площі деяких елементарних фігур

Форма перерізу

Площа перерізу

Положення центру ваги

F=bh

Центр симетрії прямокутника (на перетині діагоналей)

Центр круга (на перетині діаметрів

 

3. Проведення досліду

1. Проводять вимірювання розмірів перерізу.

2. За визначеними розмірами будують переріз та розбивають його на елементарні частини.

3. Для кожної з частин визначають положення центру ваги та її площу.

4. За формулами (4¢) визначають положення центу ваги перерізу.

5. Здійснюють експериментальну перевірку розрахунку положення центру ваги перерізу. Для цього наносять на переріз отриманий при розрахунку центр ваги та, використовуючи штатив, проводять експериментальну перевірку (рис.3).

Рис. 3. Експериментальна перевірка положення центру ваги

4. Оформлення звіту

Звіт про лабораторну роботу включає:

1.     Назву і мету роботи.

2.     Схему перерізу та його розміру, а також поділ його на елементарні частини.

3.     Площі елементарних частин та положення їх центів ваги.

4.     Визначення положення центру ваги перерізу.

4. Контрольні запитання

1.     Сформулюйте мету роботи.

2.     Як визначається центр ваги тіла?

3.     Як визначається центр ваги оболонки (пластинки)?

4.     Як визначається центр ваги стрижня?

5.     Сформулюйте правило від’ємних об’ємів (площ).

6.     Сформулюйте правило симетрії.

 

Лабораторна робота №7

Тема: Визначення деформацій у сталевій консолі

Мета роботи: дослідна перевірка основних гіпотез теорії згину та порівняння величин прогинів і кутів повороту перерізів, отриманих експериментально, з теоретичними значеннями.

Хід роботи

1. Теоретичні відомості

Під дією зовнішніх сил, що прикладені в одній з головних площин перерізу балки, вісь балки викривляється у тій же площині, в результаті чого точки осі переміщаються у напрямку, перпендикулярному до її початкового (недеформованого) стану (рис. 1).

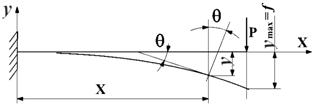
Рис. 1. Зігнута вісь балки 

Викривлену вісь балки називають зігнутою віссю або пружною лінією. Вона характеризується рівнянням y = f(x).

Переміщення центра ваги перерізу в напрямі, перпендикулярному до недеформованої осі балки, називається прогином балки в даному перерізі та позначається у. При визначенні прогину введено правило знаків: у > 0, коли прогин вверх.

Найбільший прогин балки називається стрілою прогину та позначається .

Кут, на який повертається переріз відносно свого початкового положення, називається кутом повороту перерізу. Правило знаків для визначення кута повороту має вигляд: , коли поворот перерізу проти годинникової стрілки.

Оскільки кут повороту перерізу q дорівнює куту нахилу дотичної у відповідній точці пружної ліній балки до початкового положення осі, Відповідно до геометричного змісту похідної можна записати:

; .                                                                                                                     (1)

Для визначення прогину в довільному перерізі потрібно мати рівняння пружної лінії .

Оскільки поперечні сили мало впливають на кривизну балки, то використовуючи закон Гука для чистого згину:

.                                                                                                                                 (2)

З курсу вищої математики відоме рівняння кривизни плоскої кривої:

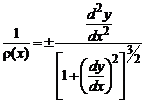.                                                                                                                       (3)

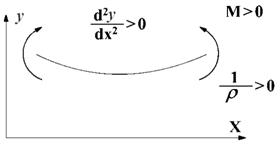
Рис. 2. Правило знаків

Оскільки за прийнятих правил знаків праві частини рівнянь (2) і (3) мають однаковий знак, то залишаючи в (3) знак плюс і прирівнюючи праві частини, одержимо точне рівняння пружної лінії балки:

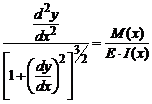                                                                                                                      (4)

Рівняння (4) для малих деформацій балки можна спростити, враховуючи, що  та нехтуючи похідними вищих порядків. Таким чином, отримаємо:

.                                                                                                                                 (5).

Це рівняння називається основним диференційним рівняння пружної лінії балки. Інтегруючи рівняння, одержимо вирази для кута повороту перерізу і прогину:

,                                                                                                                    (6)

.       (7)

Сталі  і  визначаються з умов закріплення балки та називаються геометричними початковими параметрами, оскільки характеризують значення кута повороту та прогину у крайній лівій точці балки (де розміщений початок координат) (рис. 3).

Рис. 3. Геометричні початкові параметри балки-консолі

2. Підготовка досліду

Для проведення досліду необхідні:

1.      Установка: При виконанні роботи використовується установка типу СМ-76 (рис. 4). Зразок являє собою консоль прямокутного поперечного перерізу. Балка деформується від дії зосередженої сили Р. Для визначення прогинів використовуються індикатори (механічного типу або електронні), що встановлені за допомогою штативів у точках В та С. Для визначення кута повороту індикатор встановлений у точці D, який сприймає стрижня, закріпленого на балці в перерізі, що розглядається.

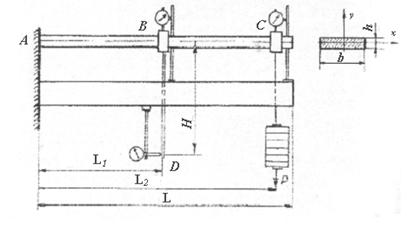
Рис. 4. Балка-консоль

2.      Прилади: для вимірювання деформацій необхідні три індикатори, що можуть бути як електронними, так і механічними. Ці прилади визначають переміщення точок перерізу при прикладанні навантаження — зміну положення тіла у деформованому стані у порівнянні з недеформованим.

3. Проведення досліду

1. До початку досліду проводять заміри робочої частини балки: ширини b та товщини h. Крім того, слід визначити відстані від точки защемлення до точки прикладання навантаження та точок визначення прогинів та кута повороту.

2. Приступаючи до проведення досліджень, необхідно визначити величину максимальної сили, яку можна прикладати до балки, не викликаючи в ньому напружень, більших від границі пропорційності:

,                                                                                                                                    (8)

де σпц = 200 МПа=2000 кг/см2 —  межа пропорційності маловуглецевої сталі, Mmax — максимальний згинальний момент від дії зосередженої сили (виникає у точці защемлення),  — момент опору перерізу.

3. Прикласти до зразка початкове навантаження. При цьому зафіксувати перші покази приладів. Надалі плавне навантаження зразка вести ступенями з постійним приростом ΔР. Для кожного ступеня навантаження збільшувати до виникнення у взірці напружень, які становлять 65–80% значення границі пропорційності. При цьому звернути увагу на те, що однаковим приростам навантажень повинні відповідати однакові прирости деформацій згідно закону Гука. Результати розрахунків занести до таблиці 1.

4. Підрахувати для кожного індикатора окремо всі прирости деформацій, які викликані приростами навантажень; визначити їх середні значення, що характеризуватимуть дослідні значення прогинів:

,                                                                                                                       (9)

де ΔуС – прирости деформацій за показами індикатора, розміщеного у точці С; n – кількість зафіксованих приростів деформацій (4–5).

Для визначення кута повороту використати формулу:

,                                                                                                                       (10)

де ΔуD – прирости деформацій за показами індикатора, розміщеного у точці D; n – кількість зафіксованих приростів деформацій (4–5), H — довжина стрижня, прикріпленого до балки.

4. Оформлення звіту

Звіт про лабораторну роботу включає:

1.     Назву і мету роботи.

2.     Схему установки для визначення переміщень перерізів консолі.

3.     Визначення максимального навантаження Pmax.

4.     Попередні дані:

a.          матеріал зразка;

b.         модуль пружності матеріалу Е;

c.          розміри зразка b і h;

d.         момент інерції J та момент опору W перерізу;

e.          відстані від защемлення до перерізів, в яких визначаються переміщення, і до перерізу, в якому прикладається навантаження L1, L2;

f.           розрахункова довжина кутомірного стрижня.

5.     Теоретичне значення прогину і кута повороту, отримані за формулами (6) та (7).

6.     Порівняння дослідних та теоретичних значень.

7.     Висновки.

Таблиця 1.

№

Наван­тажен­ня,

Р (кг)

Приріст наванта­ження ΔР, (кг)

Прогин в перерізі С, мм

Кут повороту в перерізі В, рад

Відлік індикатора, yC

Приріст відліку індикатора, ΔyC

Відлік індикатора, yD

Приріст відліку індикатора, ΔyD

1

 

 

 

 

 

 

2

 

 

 

 

 

 

3

 

 

 

 

 

 

4

 

 

 

 

 

 

5

 

 

 

 

 

 

4. Контрольні запитання

1.    Сформулюйте мету роботи.

2.    Якими приладами визначаються деформації при дослідженнях?

3.    Що таке пружна лінія балки?

4.    Що таке прогин?

5.    Що таке кут повороту?

6.    Що таке стріла прогину?

7.    Як записується диференціальне рівняння зігнутої осі балки?

8.    Що таке геометричні початкові параметри?

9.    Яке правило знаків використовується при визначенні прогину?

10.             Яке правило знаків використовується при визначенні кута повороту?

11.             Звідки визначається значення допустимого навантаження?


Лабораторна робота №8

Тема: Визначення деформацій простої балки при плоскому згині

Мета роботи: визначення лінійних та кутових переміщень у перерізах балки при згині і порівняння дослідних значень з теоретичними.

Хід роботи

1. Теоретичні відомості

Дія зовнішніх сил, які прикладені в одній з головних площин перерізу балки, спричиняє викривлення осі балки у тій же площині, в результаті чого точки осі переміщаються у напрямку, перпендикулярному до її початкового (недеформованого) стану (рис. 1).

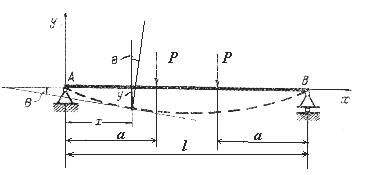
Рис. 1. Зігнута вісь балки 

Викривлену вісь балки, що називається зігнутою віссю або пружною лінією характеризується рівнянням y = f(x).

Найбільший прогин балки називається стрілою прогину та позначається . Для простої балки стріла прогину виникає у точці прикладання сили.

Кут, на який повертається переріз відносно свого початкового положення, називається кутом повороту перерізу і позначається q. На відміну від балки-консолі в опорних перерізах кут повороту має відмінне від нульового значення.

Використовуючи закон Гука для чистого згину:

,                                                                                                                                 (1)

Та враховуючи рівняння кривизни плоскої кривої:

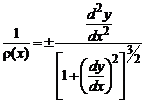,                                                                                                                       (2)

Рис. 2. Правило знаків

можна отримати точне рівняння пружної лінії балки у вигляді:

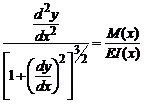                                                                                                                        (3)

Спростивши рівняння (3), враховуючи малість деформацій балки, можна отримати основним диференційним рівняння пружної лінії балки:

                                                                                                                                     (4).

Інтегруючи рівняння, одержимо вирази для кута повороту перерізу і прогину:

,                                                                                                                    (5)

.                                                                                                               (6)

Сталі  і , що визначаються з умов закріплення балки, називаються геометричними початковими параметрами та характеризують значення кута повороту та прогину у крайній лівій точці балки (де розміщений початок координат) (рис. 2).

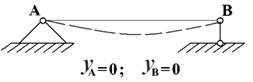
Рис. 3. Геометричні початкові параметри простої балки

 

2. Підготовка досліду

Для проведення досліду необхідні:

1.                               Установка: Робота виконується на установці СМ-4 (рис. 4), яка складається з таких основних частин: сталевої балки (1) прямокутного поперечного перерізу, яка шарнірно опирається на рухому (2) та нерухому (3) опори; двох індикаторних стійок (4); двох гирьових підвісок (5). Рухомій стояк може переміщатися по направляючій планці (6), змінюючи величину прольоту. Вимірювання кута повороту опорних перерізів проводиться за допомогою індикатора (7). Всі частини установки прикріплюються до основи (9).

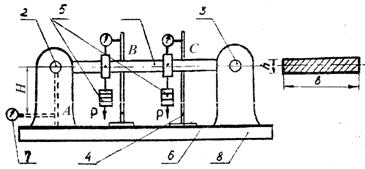
Рис. 4. Проста балка

2.                               Прилади: для вимірювання деформацій необхідні три індикатори, що можуть бути як електронними, так і механічними. Ці прилади визначають переміщення точок перерізу при прикладанні навантаження — зміну положення тіла у деформованому стані у порівнянні з недеформованим.

3. Проведення досліду

1. До початку досліду проводять заміри робочої частини балки: ширини b та товщини h. Крім того, слід визначити відстані від опорних перерізів до точок прикладання навантаження та точок визначення прогинів.

2. Приступаючи до проведення досліджень, необхідно визначити величину максимальної сили, яку можна прикладати до балки, не викликаючи в ньому напружень, більших від границі пропорційності:

,                                                                                                                                    (7)

де σпц = 200 МПа = 2000 кг/см2 — межа пропорційності маловуглецевої сталі, Mmax — максимальний згинальний момент від дії зосередженої сили (виникає у точці защемлення),  — момент опору перерізу.

3. Прикласти до зразка початкове навантаження. При цьому зафіксувати перші покази приладів. Надалі плавне навантаження зразка вести ступенями з постійним приростом ΔР. Для кожного ступеня навантаження збільшувати до виникнення у взірці напружень, які становлять 65–80% значення границі пропорційності. При цьому звернути увагу на те, що однаковим приростам навантажень повинні відповідати однакові прирости деформацій згідно закону Гука. Результати розрахунків занести до таблиці 1.

4. Підрахувати для кожного індикатора окремо всі прирости деформацій, які викликані приростами навантажень; визначити їх середні значення, що характеризуватимуть дослідні значення прогинів у точках В та С:

, ,         (8)

де ΔуС, ΔуВ – прирости деформацій за показами індикаторів, розміщені у точках В та С; n – кількість зафіксованих приростів деформацій (4–5).

Для визначення кута повороту використати формулу:

,                                                                                                                       (9)

де ΔуА – прирости деформацій за показами індикатора, розміщеного у точці А; n – кількість зафіксованих приростів деформацій (4–5), H — довжина стрижня, прикріпленого до балки.

4. Оформлення звіту

Звіт про лабораторну роботу включає:

1.     Назву і мету роботи.

2.     Схему установки для визначення деформацій у простій балці.

3.     Визначення максимального навантаження Pmax.

4.     Попередні дані:

g.          матеріал зразка;

h.         модуль пружності матеріалу Е;

i.            розміри зразка b і h;

j.            момент інерції J та момент опору W перерізу;

k.         відстані від опор до перерізів, в яких визначаються переміщення та прикладаються навантаження;

l.            розрахункова довжина кутомірного стрижня.

5.     Теоретичне значення прогину і кута повороту, отримані за формулами (6) та (7).

6.     Порівняння дослідних та теоретичних значень.

7.     Висновки.

Таблиця 1.

№

Наван­тажен­ня,

Р (кг)

Приріст наванта­ження ΔР, (кг)

Прогин в перерізі В, мм

Кут повороту в перерізі А, рад

Прогин в перерізі С, мм

Відлік індика­тора, yВ

Приріст відліку індика­тора, ΔyВ

Відлік індика­тора, yА

Приріст відліку індика­тора, ΔyА

Відлік індика­тора, yС

Приріст відліку індикато­ра, ΔyС

1

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

4. Контрольні запитання

1.     Сформулюйте мету роботи.

2.     Якими приладами визначаються деформації при дослідженнях?

3.     Що таке пружна лінія балки?

4.     Що таке прогин та кут повороту?

5.     Де виникає у простій балці стріла прогину?

6.     Як записується диференціальне рівняння зігнутої осі балки?

7.     Які геометричні початкові параметри для простої балки?

8.     Яке правило знаків використовується при визначенні прогину та кута повороту?

9.     На основі чого визначається значення допустимого навантаження?


Лабораторна робота №9

Тема: Побудова пружної лінії консольної балки при плоскому згині

Мета роботи: побудувати пружну лінію консольної балки при плоскому згині на основі теоретичних розрахунків та експериментальних даних.

Хід роботи

1. Теоретичні відомості

Зовнішні сили, що прикладені до балки спричиняють  викривлення осі балки у тій же площині, в результаті чого точки осі переміщаються у напрямку, перпендикулярному до її початкового (недеформованого) стану (рис. 1).

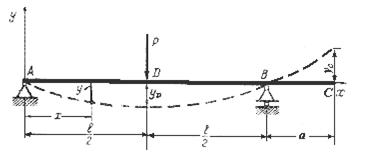
Рис. 1. Зігнута вісь балки 

Викривлену вісь балки, що називається зігнутою віссю або пружною лінією характеризується рівнянням y = f(x).

Для побудови пружної лінії балки використовують основне диференційне рівняння пружної лінії балки:

,                                                                                                                                   (1).

інтегруючи яке можна записати:

.                                                                                                               (2)

Сталі  і , що визначаються з умов закріплення балки, називаються геометричними початковими параметрами та характеризують значення кута повороту та прогину у крайній лівій точці балки (де розміщений початок координат) (рис. 2).

Рис. 3. Геометричні початкові параметри простої балки

Для побудови пружної лінії балки необхідно записати вирази для згинального моменту у перерізі на відстані х та про інтегрувати диференціальне рівняння пружної лінії. Для визначення геометричних початкових параметрів необхідно слід використати умови відсутності прогинів у опорних перерізах.

2. Підготовка досліду

Для проведення досліду необхідні:

3.                               Установка: Робота виконується на установці СМ-6 (рис. 4), яка складається з таких основних частин: сталевої балки прямокутного поперечного перерізу, яка шарнірно опирається на рухому та нерухому опори; двох індикаторних стійок; гирьової підвіски. Рухомій стояк може переміщатися по направляючій планці, змінюючи величину прольоту. Всі частини установки прикріплюються до основи.

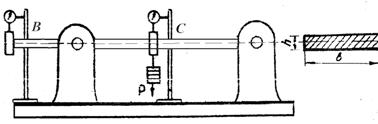
Рис. 4. Консольна балка

4.                               Прилади: для вимірювання деформацій необхідні три індикатори, що можуть бути як електронними, так і механічними. Ці прилади визначають переміщення точок перерізу при прикладанні навантаження — зміну положення тіла у деформованому стані у порівнянні з недеформованим.

3. Проведення досліду

1. До початку досліду проводять заміри робочої частини балки: ширини b та товщини h. Крім того, слід визначити відстані від опорних перерізів до точок прикладання навантаження та точок визначення прогинів.

2. Приступаючи до проведення досліджень, необхідно визначити величину максимальної сили, яку можна прикладати до балки, не викликаючи в ньому напружень, більших від границі пропорційності:

,                                                                                                                                    (3)

де σпц = 200 МПа = 2000 кг/см2 — межа пропорційності маловуглецевої сталі, Mmax — максимальний згинальний момент від дії зосередженої сили (виникає у точці защемлення),  — момент опору перерізу.

3. Прикласти до зразка початкове навантаження. При цьому зафіксувати перші покази приладів. Надалі плавне навантаження зразка вести ступенями з постійним приростом ΔР. Для кожного ступеня навантаження збільшувати до виникнення у взірці напружень, які становлять 65–80% значення границі пропорційності. При цьому звернути увагу на те, що однаковим приростам навантажень повинні відповідати однакові прирости деформацій згідно закону Гука. Результати розрахунків занести до таблиці 1.

4. Підрахувати для кожного індикатора окремо всі прирости деформацій, які викликані приростами навантажень; визначити їх середні значення, що характеризуватимуть дослідні значення прогинів у точках В та С:

, ,         (4)

де ΔуС, ΔуВ – прирости деформацій за показами індикаторів, розміщені у точках В та С; n – кількість зафіксованих приростів деформацій (4–5).

4. Оформлення звіту

Звіт про лабораторну роботу включає:

1.     Назву і мету роботи.

2.     Схему установки для визначення деформацій у простій балці.

3.     Визначення максимального навантаження Pmax.

4.     Попередні дані:

m.       матеріал зразка;

n.         модуль пружності матеріалу Е;

o.         розміри зразка b і h;

p.         момент інерції J та момент опору W перерізу;

q.         відстані від опор до перерізів, в яких визначаються переміщення та прикладаються навантаження.

5.     Теоретичне значення прогину і кута повороту, отримані за формулами (4).

6.     Порівняння дослідних та теоретичних значень (шляхом побудови пружної лінії балки, отриманої при теоретичних розрахунках та експериментальних дослідженнях.

7.     Висновки.

Таблиця 1.

№

Наван­тажен­ня,

Р (кг)

Приріст наванта­ження ΔР, (кг)

Прогин в перерізі В, мм

Прогин в перерізі С, мм

Відлік індика­тора, yВ

Приріст відліку індика­тора, ΔyВ

Відлік індика­тора, yС

Приріст відліку індикато­ра, ΔyС

1

 

 

 

 

 

 

2

 

 

 

 

 

 

3

 

 

 

 

 

 

4

 

 

 

 

 

 

5

 

 

 

 

 

 

4. Контрольні запитання

1.     Сформулюйте мету роботи.

2.     Чим визначаються деформації при дослідженнях?

3.     Що таке пружна лінія балки?

4.     Як записується диференціальне рівняння зігнутої осі балки?

5.     Які геометричні початкові параметри для консольної балки?

6.     На основі чого визначається значення допустимого навантаження?


ДОДАТКИ

Додаток 1. Підготовка випробувальної машини МИ-40КУ до проведення випробувань

 

1. Ввімкнути комп’ютер і випробувальну машину МИ-40КУ.

2. Після завершення завантаження операційної системи запустити програмне забезпечення МИ-40КУ: "Пуск" – "Программы" – "Випробувальна машина МИ-40КУ".

3. Встановити зразок в затискачі машини (в випадку розтягу чи кручення), або поставити зразок на нижню робочу плиту машини (у випадку стиску) та користуючись кнопками управління, розміщеними безпосередньо на машині МИ-40КУ встановити верхню робочу плиту машини в потрібне положення. Важливо не здеформувати зразок під час встановлення. Для цього залишити невеличкий проміжок між верхньою плитою та взірцем (0,5...1мм)

4. Вибрати пункт головного меню "Файл" – "Создать". У вікні, що з’явилось необхідно вибрати тип досліду (доступні типи: "Розтяг", "Стиск", "Кручення", "Розтяг з крученням", "Стиск з крученням") і ввести дані про зразок (розміри, матеріал, та ін.).

Примітка: Якщо вікно створення досліду не з’явилось, і програма видала повідомлення "Не удается установить связь с МИ-40КУ", то це означає, що не вибраний СОМ-порт, або він був вибраний невірно. Для вибору або зміни СОМ-порта потрібно в головному меню натиснути "Конфигурация" – "Выбор СОМ-порта" і у вікні, що з’явиться, вибрати потрібний порт (як правило, це або СОМ1, або СОМ2)

5. Перевірити нульові покази датчиків осьового (3) та обертового навантажень (10). Якщо покази датчиків відрізняються від нульових – відрегулювати їх за допомогою регуляторів, розміщених на машині.

6. Користуючись кнопками управління машиною (8) (див. дод. 2) провести більш точне встановлення зразка на малій швидкості (4–5мм/хв). Встановлення зразка вважається завершеним в момент початку зростання навантаження.

7. Встановити робочу швидкість досліду (рекомендоване значення при розтягу-стиску 2..4мм/хв, при крученні 0,01об/хв)

8. Після завершення досліду зберегти результати ("Сохранить как"), та звільнити зразок від затискачів.

 

Додаток 2. Інтерфейс програмного забезпечення

випробувальної машини МИ-40КУ

 

Машина МИ-40КУ має підключення до комп’ютера для керування машиною і зняття показань датчиків. Для цього призначено програмне забезпечення, інтерфейс якого показано на рис. 1.

 

 

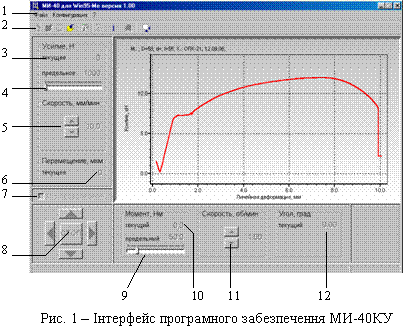
1. Головне меню. Складається із підменю "Файл", "Конфигурация" "?"

· підменю "Файл":

o                        "Создать" – створення нового досліду. Після вибору цього пункту меню з’являється вікно, де потрібно вибрати тип досліду ("Розтяг", "Стиск", "Кручення", "Розтяг з крученням", "Стиск з крученням") і ввести дані про зразок (розміри, матеріал, та ін.)

o                        "Открыть" – можна відкрити збережені результати попередніх дослідів.

o                        "Сохранить как" – збереження результатів досліду.

o                        "Сохранить в виде BMP" – збереження вигляду діаграми у графічний файл.

o                        "Печать" – друк діаграми на принтері.

o                        "Закрыть" – завершення досліду.

o                        "Выход" – вихід із програми.

· підменю "Конфигурация":

o                        "Выбор СОМ-порта" – вибір СОМ-порту, до якого підключена машина МИ-40КУ.

· підменю "?" містить в собі лише один пункт "О программе".

2.  Панель кнопок. Більшість кнопок дублюють відповідні пункти з головного меню. Кнопка  призначена для встановлення початкового масштабу діаграми.

3.  Індикація осьового зусилля на зразок, Н.

4.  Встановлення граничного осьового зусилля. При досягненні граничного значення осьовий рух станини автоматично зупиняється.

5.  Встановлення швидкості осьового руху. Має фіксовані значення. Якщо встановлено значення швидкості більше 10 мм/хв, то при ввімкненні руху випробувальної частини це значення автоматично буде встановлене в 10 мм/хв.

6.  Індикація осьового переміщення випробувальної частини (осьове видовження), мм.

7.  "Образец установлен" ("Зразок встановлено") – для того, щоб мати змогу розпочати дослід і виставити граничні значення зусиль, цей перемикач повинен бути ввімкнений. Вмикати його можна лише після того, як зразок встановлений і закріплений в захватах машини.

8.  Група кнопок управління машиною МИ-40КУ (рис. 2).

9.   Встановлення граничного крутного моменту, який подається на зразок. При досягненні граничного значення обертальний рух станини автоматично зупиняється.

10.                Індикація значення крутного моменту, Н·м.

11.                Встановлення швидкості обертального руху. Має фіксовані значення. Якщо встановлено значення швидкості більше 1 об/хв, то при ввімкненні руху випробувальної частини це значення автоматично буде встановлене в 1 об/хв.

12.                Індикація кута повороту випробувальної частини (кут закручування), град.