4.3. Матеріали і конструкції деталей черв’ячної передачі.

 Критерії роботоздатності та розрахунків

 

Наявність високих швидкостей ковзання у зачепленні ставить до матеріалів черв’ячної передачі такі вимоги, як високі антифрикційні властивості, стійкість проти спрацювання та стійкість до заїдання.

Черв’яки здебільшого виготовляють із якісних вуглецевих сталей (45, 50, 40Г2), а у передачах відповідального призначення – із легованих сталей (40Х, 40ХН, 35ХГСА та ін.). Термообробка до твердості H₁ ≥ (45.. 55) HRC і подальше шліфування та полірування робочих поверхонь витків черв’яка дозволяють суттєво підвищити несучу здатність та довговічність передачі, оскільки зменшують можливість заїдання робочих поверхонь у контакті. У допоміжних, невідповідальних та тихохідних передачах можуть використовуватись черв’яки з твердістю витків Н₁ = (300...320)НВ.

Вінці черв’ячних коліс виготовляють переважно з бронзи, а інколи з латуні та чавуну. Олов’яні бронзи БрО10НІФ1, БрО10Ф1 та інші є кращими матеріалами для вінців черв’ячних коліс при високих швидкостях ковзання (v_s > 5 м/с), однак вони дорогі та дефіцитні. Тому такі бронзи використовують лише для відповідальних черв’ячних передач. Менш дефіцитні і дешевші безолов’яні бронзи БрА10Ж4Н4, БрА9ЖЗЛ та ін. Вони мають достатньо високі показники міцності, але дещо гірші антифрикційні властивості і меншу здатність до пропрацьовування. Безолов’яні бронзи вимагають високих твердості та чистоти робочих поверхонь витків черв’яка і застосовуються при се­редніх швидкостях ковзання v_s = (2...5) м/с.

Для допоміжних, малонавантажених та тихохідних (v_s < 2 м/с) черв’ячних передач можливе виготовлення черв’ячного колеса із чавуну (СЧ15, СЧ18) або пластмас (текстоліту, поліамідів).

Конструктивно черв’яки виготовляють у більшості випадків разом із валом як одну деталь (рис. 6, а) і лише у рідких випадках насадними
(рис. 6, б).

З метою економії кольорових металів черв’ячні колеса виготовля­ють складеними з двох частин (рис. 81, в, г): бронзового вінця, який з’єднується з чавунним або сталевим колісним центром по відповід­ній посадці і закріплюється додатково гвинтами або болтами. Можли­ві інші варіанти з’єднання колісного центра з вінцем черв’ячного колеса. При малих діаметрах черв’ячних коліс або чавунних колесах застосовують суцільні черв’ячні колеса (рис. 6, д).

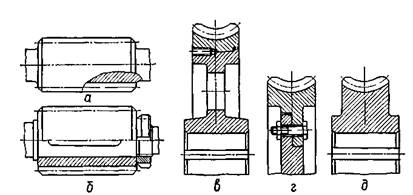
Рис. 6. Конструкції черв’яків та черв’ячних коліс

 

Зубці черв’ячних коліс – найслабкіші елементи у черв’ячних передачах. Значні швидкості ковзання в зачепленні спричинюють спрацювання та заїдання. Ці явища посилюються невідповідними умовами змащування контакту, бо напрям швидкості ковзання утворює малий кут із напрямом лінії контакту витків та зубців.

Обмеження можливості виникненню заїдання в зачепленні може бути досягнуте не тільки вибором відповідних матеріалів черв’яка та колеса, але й обмеженням контактних напружень. Інтенсивність спрацювання зубців черв’ячного колеса також залежить від рівня контактних напружень. Отже, для забезпечення тривалої роботоздатності черв’ячної передачі слід обмежити контактні напруження на активних поверхнях зубців черв’ячного колеса. Треба брати до уваги, що несуча здатність черв’ячних передач із колесами, виготовленими з олов’яних бронз, обмежується втомною міцністю активних поверхонь зубців, а передач із колесами, виготовленими з безолов’яних бронз та чавунів – заїданням. Імовірність поломок зубців черв’ячного коле­са від дії циклічних напружень згину суттєва тільки для маломодульних черв’ячних коліс.

Для черв’ячних передач виконують такі розрахунки:

1) розрахунок активних поверхонь зубців черв’ячного колеса на онтактні втому та міцність при дії максимального навантаження;

2) розрахунок зубців черв’ячного колеса на втому при згині та на міцність при згині максимальним навантаженням.

При розрахунку на контактну втому активних поверхонь зубців черв’ячних коліс, виготовлених із олов’яних бронз, допустиме контактне напруження визначають за формулою:

[σ]_H = [σ]_HO К_HL,                                               (19)

де [σ]_HO – допустиме контактне напруження для бази випробувань n_ho = 10⁷;

 k_hl – коефіцієнт довговічності.

Значення [σ]_HO залежить від границі міцності σ_в бронзи та коефіцієнта c_v інтенсивності спрацювання зубців: с_v = 0,95 при v_s = 5 м/с; с_v = 0,88 при
v_s = 6 м/с; с_v= 0,83 при v_s = 7 м/с; c_v = 0,80 при v_s ≥ 8 м/с. При виконанні проектного розрахунку, коли розміри передачі ще невідомі, орієнтовне значення швидкості ковзання v_s, м/с, можна дістати за формулою:

 v_s = (4ω_l /10³)                                           (20)

де ω_l – кутова швидкість черв’яка, рад/с; T₂ – обертовий момент на веденому валу передачі, Н·м.

Коефіцієнт довговічності рекомендують визначати за співвідношенням:

К_HL=,

де N_HE – еквівалентне число циклів навантаження зубців черв’яч­ного колеса за строк служби передачі. Коефіцієнт довговічності обмежується значеннями   0,67≤ К_HL ≤ 1,15.

Для зубців черв’ячних коліс, виготовлених із твердих безолов’яних бронз та чавунів, допустиме контактне напруження вибирають з умови опору заїданню залежно від швидкості ковзання v_s і беруть [σ]_H = [σ]_HO.

Для зубців черв’ячних коліс, ви­готовлених із бронз, допустиме напруження для розрахунку на втому при згині визначають за формулою:

[σ]_F = [σ]_FO · К_FL.                                              (22)

Тут [σ]_FO – допустиме напруження для бази випробувань, що дорівнює 10⁶, залежить від границі міцності σ_в та текучості σ_т бронз; К_FL – коефіцієнт довговічності при розрахунку на згин,

К_FL =.                                                (23)

Еквівалентне число циклів N_FE навантаження зубців за строк служби передачі, а коефіцієнт довговічності беруть у межах 0,54 ≤ К_FL ≤ 1. Для зубців чавунних черв’ячних коліс [σ]_F = [σ]_Fo. Допустимі граничні напруження згину [σ]_{F mах} = 0.8σ_T

У навантаженій черв’ячній передачі сила взаємодії між витками черв’яка та зубцями колеса розподіляється вздовж лінії їхнього контакту. Таку розподілену силу замінимо зосередженою і прикладеною до зубця черв’ячно­го колеса у його середньому нормальному до осі перерізі. При цьому сили тертя у зачепленні не враховуються.

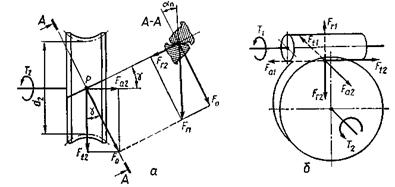
Рис. 7. Зусилля на зубці черв’ячкого колеса і витки черв’яка

 

Дія обертового моменту Т₂ на валу черв’ячного колеса спричинює появу нормальної сили F_n з боку витка черв’яка на зубець колеса. Ця сила діє у площині А – А, нормальній до лінії зубця (рис. 7, а), напрямлена по нормалі до профілів витка та зубця у точці їх контакту і утворює кут зачеплення α_n з перпендикуляром до лінії центрів чер­в’яка і черв’ячного колеса.

Замінимо силу F_n  двома її взаємно перпендикулярними складовими F_r2 і F_o. які перенесемо на схему черв’ячного колеса. Тут сила F_r2  проектується в точку Р, а сила F_o лежить у площині А – А і напрямлена по дотичній до початкового циліндра колеса. Зобразимо силу F_o також у вигляді двох взаємно перпендикулярних складових F_t2 і F_а2. Отже, замість нормальної сили маємо три її взаємно перпендикулярні складові F_t2, F_r2 і F_a2.

Колова сила на черв’ячному колесі визначається через обертовий момент:

F_t2 = 2T₂/d₂.                                             (24)

Осьова сила на черв’ячному колесі подається через колову силу:

F_a2 = F_t2 · tg γ.                                           (25)

Для визначення радіальної сили F_r2 попередньо запишемо
F₀ = F_t2 /cos γ, а тоді дістанемо:

F_r2 = F₀ tg α_n = F_t2 tg α_n / cos γ.

Враховуючи, що tgα_n /cosγ = tg α, де α = 20^o – кут зачеплення у площині, перпендикулярній до осі колеса, запишемо вираз для визначення радіальної сили:

F_r2 = F_t2 · tg α.                                             (26)

Нормальна сила F_n на зубець колеса дорівнює сумі складових сил F_t2, F_r2 і F_a2, а її модуль визначається за формулою:

F_n = F₀/cos α_n = F_t2 /(cos α_n · cos γ).                        (27)

На витки черв’яка з боку зубців колеса діють такі самі сили, але в протилежному напрямі (рис. 7, б), до того ж деякі з них міняють свою назву.

Колова сила на черв’яку дорівнює осьовій силі на черв’ячному колесі:

F_t1 = F_a2 = F_t2 · tgγ.                                     (28)

Осьова сила на черв’яку дорівнює коловій силі на колесі:

F_a1= F_t2 = 2T₂/d₂.                                      (29)

Радіальна сила на черв’яку дорівнює радіальній силі на колесі:

F_r1=F_r2 = F_t2 · tgα.                                    (30)

Розрахункове навантаження на зубці черв’ячного колеса. За розрахункове навантаження на зубці черв’ячного колеса беремо максимальне значення питомої сили, розподіленої по лінії контакту,

q = (F_n / l_∑) · K_β · K_v.                                   (31)

де F_n – нормальна сила на зубці згідно з формулою (27); l_∑ – сумарна довжина контактних ліній у зачепленні. Коефіцієнт K_β, що враховує розподіл навантаження по ширині вінця черв’ячного колеса, та коефіцієнт K_v динамічного навантаження мають той самий зміст, що і в зубчастих передачах.

Наближено сумарну довжину контактних ліній у зачепленні черв’ячної передачі можна визначити за формулою:

l_∑ = b₂ · ε_α/cosγ,                                            (32)

де b₂ – ширина вінця черв’ячного колеса; γ – кут нахилу зубців, який дорівнює ділильному куту підйому витків черв’яка; ε_α  – тор­цевий коефіцієнт перекриття, який у середній площині черв’ячного колеса становить 1,8–2,2.

У виразі (32) не врахована зігнута форма зубців черв’ячного колеса, але вона компенсується неповнотою дотикання витків та зуб­ців по дузі обхвату черв’яка 2δ Підставляючи (27) і (32) у вираз (31), дістанемо:

q = w_t / (ε_α cos α_n).                                            ( 33)

Тут w_t – питома розрахункова колова сила, що визначається за формулою:

w_t = (F_t2 / b₂)K_βK_v.                                            (34)

За аналогією із зубчастими передачами вирази для розрахункового навантаження та питомої розрахункової колової сили записують у вигляді:

– при розрахунку активних поверхонь зубців на контактну втому:

q_H = w_{H  t} /(ε_α · cos α_n);    w_{H t} = (F_{H t2} /b₂) · К_{H β} ·  К_HV;         (35)

– при розрахунку зубців на втому при згині:

q_F = w_{F  t} /(ε_α · cos α_n);    w_{F t} = (F_{F t2} /b₂) · К_{F β}  ·К_FV                   (36)

Колові сили F_{H t2} і F_{F t2} мають вигляд:

F_{H t2} = 2T_2H /d₂;    F_{F t2} = 2T_2F/d₂,                (37)

де обертові моменти T_2H = T_2F = T₂  і будуть дорівнювати макси­мальному тривало діючому обертовому моменту відповідно до заданого режиму навантаження передачі.

Для черв’ячної передачі беруть К_Hβ = К_Fβ і К_HV = К_FV.

Коефіцієнт, що враховує розподіл навантаження по ширині вінця черв’ячного колеса,

K_β = 1+(z₂/θ)³ · (1–x).                                          (38)

Тут z₂ – число зубців черв’ячного колеса; θ – коефіцієнт деформації черв’яка; х – коефіцієнт, що враховує вплив режиму роботи передачі на припрацьовування зубців.

Коефіцієнт K_V динамічного навантаження зачеплення черв’ячної передачі визначають залежно від ступеня точності передачі та швидкості ковзання.

Стійкість проти втомного викришування та проти заїдання активних поверхонь зубців черв’ячного колеса забезпечується при виконанні загальної умови:

σ_H =Z_M·  ≤ [σ]_H.

Для черв’ячної передачі питоме розрахункове навантаження на зубці колеса визначають за виразом (35):

q = q_H = w_Ht / (ε_α · cos α_n).

Радіус кривини робочої поверхні витків в осьовому перерізі ρ₁ = ∞, а радіус кривини профілів зубців черв’ячного колеса ρ₂, можна знайти за формулою (11) для зубців косозубого зубчастого колеса, замінивши кут β на γ. Тоді матимемо:

1/ρ_зв = 1/ρ₁ + 1/ρ₂ = 1/ρ₂ = 2 cos γ / (d₂ · sin α_n).

Після підстановки q і 1/ρ_зв  у загальну умову, дістанемо:

σ_H =Z_M · ≤  [σ]_H.

Взявши cos α_n· sin α_n = 0,5 sin 2α_n та позначивши:

Z_H=;   Z_ε=,

будемо мати остаточну залежність для розрахунку активних поверхонь зубців на контактну втому у такому вигляді;

σ_H =Z_MZ_HZ_ε ≤  [σ]_H .                                (39)

де Z_M – коефіцієнт, що враховує механічні властивості матеріалів черв’яка та черв’ячного колеса; для поєднання матеріалів сталь –бронза (Е₁ = 2,1·10⁵ МПа;

Е₂ = 0,9·10⁵ МПа; μ₁ = 0,28; μ₂= 0,33) Z_M = 210 МПа^1/2;   для матеріалів сталь – чавун (Е₁ = 2,1·10⁵ МПа; Е₂ = 10⁵ МПа; μ₁ = 0,28; μ₂= 0,27)
Z_M =  215 МПа^1/2;

Z_H – коефіцієнт форми спряжених поверхонь витків черв’яка та зубців колеса,

Z_H = 1,8 для усе­реднених значень γ; Z_ε – коефіцієнт сумарної довжини контактних ліній у зачепленні; у розрахунках беруть Z_ε = 0,75 (для мінімального значення коефіцієнта торцевого перекриття ε_α = 1,8).

Виконання умови (39) при перевірному розрахунку черв’ячної передачі забезпечує стійкість активних поверхонь зубців колеса проти втомного руйнування та заїдання. При невиконанні цієї умови треба змінити розміри передачі.

Розрахунок активних поверхонь зубців черв’ячного колеса на кон­тактну міцність при дії максимального навантаження виконується аналогічно зубчастим передачам:

σ_Hmax = σ_H ≤  [σ] _Hmax,                                  (40)

де σ_H – розрахункове контактне напруження, що визначається за виразом (39); T_2max – найбільше навантаження з числа коротко­часно діючих на валу черв’ячного колеса; [σ] _Hmax – допустиме граничне контактне напруження.

Розрахунок напружень згину зубців черв’ячного колеса ускладнюється змінною формою перерізів зубця по ширині колеса і тим, що зубець має угнуту форму. У розрахунках черв’ячне колесо розглядають як косозубе циліндричне. Витривалість при згіні:

σ_F = Y_F ·Y_β ·Y_ε ·W_Ft / m ≤ [σ]_F,                                             (41)

де w_Ft – питома розрахункова колова сила на черв’ячному колесі; m – коловий модуль зубців черв’ячного колеса (осьовий модуль черв’яка).

Коефіцієнт Y_F форми та підвищеної міцності зубців черв’ячного колеса знаходять залежно від еквівалентного числа зубців z_V2 = z₂ /cos³γ. Коефіцієнт Y_ε перекриття зубців у розрахунках можна брати 0,75.

Коефіцієнт Y_β нахилу зубців черв’ячного колеса слід визначати за виразом Y_β = (1–γ/140)/cos γ, або його можна брати Y_β ≈ 0,95 (для деякого середнього значення кута нахилу зубців γ ≈ 10⁰).

Перевірку міцності зубців при згині максимальним навантаженням можна виконати за умовою:

σ_Fmax = σ_F · (T_2max /T_{2 F} )  ≤  [σ] _{F max},                            (42)

де σ_F – розрахункове напруження згину; [σ]_Fmax – допустиме граничне напруження на згин.

У проектному розрахунку визначають міжосьову відстань черв’яч­ної передачі як основний параметр, що визначає габаритні розміри передачі. Міжосьову відстань розраховують із умови стійкості актив­них поверхонь зубців колеса проти втомного руйнування та заїдання.

Вихідні дані для проектного розрахунку черв’ячної передачі є такі: розрахункове тривало діюче навантаження Т_2H; передаточне число передачі u; тип черв’яка ZA, ZN чи ZI; типовий режим навантаження передачі та строк її служби; матеріали для черв’яка та черв’ячного колеса, за якими визначають допустиме контактне напруження.

Несуча здатність черв’ячних передач із архімедовими (ZA), конволютними (ZN) та евольвентними (ZI) черв’яками може бути оцінена за одними й тими ж розрахунковими залежностями (39), (40), (41) та (42). Відхилення результатів розрахунку від дійсних направлено на збільшення запасів міцності виготовлених та змонтованих черв’ячних передач.

Розрахункові формули для проектного розрахунку черв’ячної передачі

d₁ = 2 · а_W · q /(q + z₂);        d₂ = 2 · а_W · z₂ /(q + z₂).

Формула для визна­чення мінімальної міжосьової відстані черв’ячної передачі:

а_Wmin = К_a · (z₂/q + 1) ·.                  (43)

Тут слід брати обертовий момент T_2Н у ньютон-метрах (Н·м), допустиме напруження [σ]_H у мегапаскалях (МПа), а міжосьову відстань а_Wmin у міліметрах (мм).

Допоміжний коефіцієнт К_a визначається за виразом:

К_а = .

Для усереднених значень розрахункових коефіцієнтів беруть:

К_а = 310 МПа^1/3 – для поєднання матеріалів черв’яка та коле­са сталь – бронза;

К_а = 315 МПа^1/3 – для поєднання матеріалів сталь – чавун.

Для визначення а_Wmin треба попередньо вибрати число зубців черв’ячного колеса z₂. У силових черв’ячних передачах рекомендують
28 ≤ z₂ ≤ 80. Мінімальне число зубців z_2min = 28 обмежується умо­вою непідрізання, а максимальне число зубців z_2max = 80 – умовою обмеження габаритних розмірів передачі та забезпечення міцності зубців на згин. У деяких випадках допускається число зубців z₂ = 100... 150 і більше. При заданому передаточному числі передачі u та вибра­ному числі витків черв’яка z₁ число зубців колеса z₂ = uz₁. Число витків черв’яка z₁ = 1; 2; 4 потрібно брати по можливості більшим (підвищується ККД передачі), але так, щоб при заданому u число зубців z₂ було у рекомендованих межах.

Коефіцієнт діаметра черв’яка q вибирають із числа стандартних значень. Більші значення q рекомендують брати для насадних черв’яків або при великих передаточних числах, щоб забез­печити достатню жорсткість черв’яка.

Модуль черв’ячної передачі знаходять, виходячи з формули:

m′ = 2а_Wmin /(q+z₂).

Значення модуля узгоджують із стандартним за даними.

За розмірами, добутими в проектному розрахунку, належить виконати перевірні розрахунки.

Для того, щоб забезпечити надійну роботу черв’ячної передачі, слід надати черв’яку достатніх міцностей та жорсткості. Потреба розрахунку черв’яка на жорсткість пов’язана з тим, що черв’як у більшості випадків має порівняно малий діаметр і значну відстань між опорами.

Дія на черв’як сил, що виникають у його зачепленні з колесом, може призвести до його значного поперечного прогину, який негативно впливає на зачеплення витків та зубців і на роботу черв’ячної передачі. Тому умову достатньої жорсткості черв’яка запишемо у вигляді:

y ≤ [y],                                                  (44)

де у – розрахункова стрілка прогину черв’яка; [у] – допустима стрілка прогину за умови нормальної роботи зачеплення.

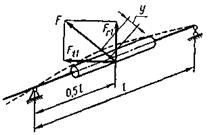
Рис. 8. До визначення прогину вала черв’яка

 

Для розрахункової схеми навантаження черв’яка (рис. 8) стрілку прогину знаходять за відомою з курсу опору матеріалів формулою:

у = F · l³ / (48 · E · I₀),                                          (45)

де F =  – рівнодійна колової та радіальної сил на черв’я­ку;

l ≈ (0,8...1,0) · d₂ – орієнтовна відстань між опорами черв’яка; Е – модуль пружності матеріалу черв’яка; I₀ = π · d⁴_f1/64 – осьовий момент інерції перерізу черв’яка без врахування впливу витків.

Формула (45) для черв’яка наближена, бо черв’як за довжиною має змінні розміри поперечних перерізів.

Допустиму стрілку прогину черв’яка визначають залежно від модуля m у межах [у] = (0,01...0,005)m.

Якщо при розрахунку виявиться, що жорсткість черв’яка недостатня
(y > [y] ), то потрібно збільшити коефіцієнт діаметра черв’яка q, або, за можливістю, зменшити відстань l між його опорами.

Загальний ККД черв’ячної передачі можна визначити за залежністю:

η = Р₂/Р₁ = η₁· η₂· η₃,                                        (46)

де Р₂, Р₁ – потужності на веденому і ведучому валах передачі відпо­відно; η₁, η₂, η₃ – ККД, що відображають втрати потужності у зачеп­ленні, підшипниках та на переміщування мастила у корпусі передачі відповідно.

Найбільшими є втрати потужності у зачепленні черв’ячної переда­чі, обумовлені ковзанням витків черв’яка по зубцях черв’ячного ко­леса. Щоб знайти ККД черв’ячного зачеплення, слід розглянути сили, які діють на виток черв’яка за умови, що черв’як є ведучим (рис. 9, а). Зубець черв’ячного колеса показаний на рисунку заштрихованою фігурою.

Сила F_о = F_n cos α_n перпендикулярна до лінії витка черв’яка, а сила тертя F_s = F_nf напрямлена вздовж лінії витка. Ці дві сили дають результуючу силу F, яка складає з вектором сили F₀ кут φ′:

tg φ′ = F_s/F₀ = f /cos α_n;             φ′ = arctg · ( f /cos α_n),           (47)

де φ′ – зведений кут тертя, а f – коефіцієнт тертя ковзання.

Розклавши силу F за напрямами колових швидкостей черв’яка та черв’ячного колеса, дістанемо колову силу F_t1 на черв’яку і осьову силу F_a1, яка дорівнює коловій силі F_t2 на черв’ячному колесі:

F_t1 = F · sin (γ + φ′);       F_a1 = F_t2 = F · cos (γ + φ′).          (48)

ККД черв’ячного зачеплення при передаванні навантаження від черв’яка до черв’ячного колеса (черв’як ведучий) можна визначити за виразом:

η₁ = T₂ · ω₂/(T₁ · ω ₁) = F_t2 ·  d₂ · ω₂ /(F_t1 · d₁ · ω₁).

Якщо у записане співвідношення підставити F_t1 і F_t2  і взяти  d₂ = mz₂,  d₁= mq,  tg γ = z₁/q  і ω₁/ω₂ = u = z₂/z₁, то матимемо остаточну формулу для визначення ККД зачеплення черв’ячної передачі:

η₁ = tg γ / tg (γ + φ′),                                  (49)

де γ – ділильний кут підйому витка черв’яка.

За аналогічними міркуваннями можна дістати формулу для ККД черв’ячного зачеплення при передаванні навантаження від черв’ячного колеса до черв’яка (черв’ячне колесо ведуче).

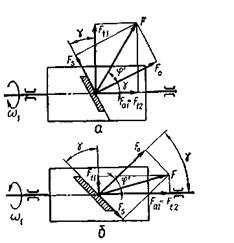
Рис. 9. До визначення ККД черв’ячної передачі

 

У цьому разі схема сил, які діють на виток черв’яка, показана на
рис. 9, б, а розрахункова формула має вигляд:

η^*₁ = [tg (γ – φ′)] / tg γ.                                 (50)

Кут тертя φ′ спадає з ростом швид­кості ковзання v_s, оскільки при цьому створюються більш сприятливі умови для утворення неперервного шару ма­стила, що розділяє поверхні зубців та витків (зменшується коефіцієнт тертя f).

Аналіз формули (50) показує, що при γ ≤ φ′ передавати рух від колеса до черв’яка неможливо, оскільки η^*₁ ≤ 0. У цьому разі здійснюється самогальмування передачі.

ККД черв’ячного зачеплення суттєво залежить від ділильного кута підйому витків черв’яка γ, тобто від числа витків z₁ та коефіцієнта діаметра черв’яка q. Середні значення ККД зачеплення залежно від числа витків черв’яка такі:

η₁= 0,70...0,75  при  z₁ = 1;         η₁ = 0,80...0,90  при  z₁ = 2...4.

Втрати потужності у підшипниках і на переміщування мастила в корпусі передачі здебільшого оцінюються   η₂η₃ = 0,95...0,96. Тому загальний ККД черв’ячної передачі рекомендують визначати за формулою:

η = (0,95.. .0,96) · tg γ/ tg (γ + φ′).                              (51)

Через значні втрати потужності за рахунок низького ККД черв’ячної передачі відбувається нагрівання корпусу передачі і мастила, що в ньому знаходиться. При підвищених температурах мастило втрачає свої мастильні властивості, що може призвести до виходу передачі з ладу. Тому для черв’ячної передачі виконують тепло­вий розрахунок. Цим розрахунком слід забезпечити умову:

t_M < [t] _M.                                               (52)

де t_M – температура мастила при усталеному режимі роботи передачі;
[t]_M – допустима температура мастила, що становить 75–85°С. Деякі спеціальні марки мастил допускають температуру до 100–110°С.

Потужність, що втрачається у передачі:

∆Р = Р₁– Р₂ = Р₁ · (1– η).

Тепловий потік, що виділяється поверхнею площі А корпусу передачі:

Ф = K · A · (t_M – t₀).

Усталений режим роботи передачі має тепловий баланс ∆Р = Ф або

Р₁ · (1– η) = K · A · (t_M – t₀).

звідки дістаємо температуру мастила:

t_M = t₀ + Р₁ · (1– η) / (K · A),                                      (53)

де Р₁ – потужність, що підводиться до передачі, Вт; K – коефіцієнт теплопередачі, K = (9...17) Вт/(м² ·°С) залежно від швидкості повітря, що омиває корпус передачі; А – площа охолоджуваної поверхні корпусу, м²;
t₀ – температура середовища, в якому працює передача, °С.

Щоб задовольнити умову (52), інколи збільшують поверхню корпусу передачі (ребристі форми корпусів), застосовують обдування корпусу вентилятором тощо. При обдуванні за допомогою вентилятора К=(25...30)Вт/(м²·°С).