 .
.
.
.
Тема 1. Прямокутні проекції основних геометричних тіл
При побудові комплексного кресленика або епюра Монжа з трьох прямокутних проекцій площину П 2 приймають нерухомою, а площини П1 та П3 суміщують з нею обертанням навколо осей x та z. Площини /поля/ проекцій П1, П2 та П3, перетинаючись по трьох лініях, задають просторову декартову систему координат (рис.1.5). Точка О є початком координат, вісь х - віссю абсцис,
вісь у - віссю ординат та вісь z - віссю аплікат. Неважко помітити, що проекції
А1 та А2 лежать на одній вертикальній лінії, а проекції А2 та А3 – на одній
горизонтальній лінії, які називаються лініями зв’язку.
Розгорнемо площини, які утворюють просторову декартову систему координат до
суміщення їх з площиною П2 (рис.1.6). Побудуємо бісектрису k кута у(-z), О,
у(-x) та зобразимо проекції точки А в площинах П1, П2 і П3. Ламана лінія зв’язку,
яка з’єднує проекції А1 та А3 складається з двох відрізків (горизонтального та вертикального) з вершиною на бісектрисі кута у(-z), О, у(-x). Частину цієї
ламаної інколи замінюють дугою кола. Таким чином, між горизонтальною та профільною
проекціями існує ламана горизонтально-вертикальна лінія зв’язку. Бісектрису
k, що є множиною вершин цих ламаних ліній, називають постійною прямою комплексного
кресленика.
Площини проекцій П1, П2 та П3
ділять тривимірний простір на вісім частин, які називаються октантами. У тих
випадках, коли точка задається координатами, можна будувати комплексний кресленик,
керуючись величиною та знаками координат, навіть не визначаючи октанту, в якому
задана точка.
Знаки координат, які відповідають тому чи іншому октанту, наведені в таблиці
1.1.
Якщо точка знаходиться в першій чверті (двохплощинна модель) або в першому (п’ятому)
октанті (трьохплощинна модель) простору при закріплених площинах проекцій, то
її горизонтальна проекція розміщується нижче, а фронтальна проекція –
вище осі х. По-іншому розміщуються проекції точок, що знаходяться в 2(6), 3(7) та
4(8) чвертях (октантах) простору. На рис.1.7 показано розташування точок в різних
чвертях простору.

Якщо одна з проекцій точки знаходиться
на осі, то точка простору належить одній із площин проекцій і розташована на
межі чвертей.
Якщо відстані від проекцій точок до осі рівні, то точка простору належить бісекторній
площині. Бісекторна площина – це площина ,
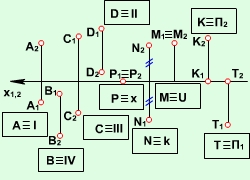
яка ділить чверті навпіл. Площина, яка проходить через 1 і 3 чверті називається 1 бісекторною площиною і позначається буквою K, площина, яка проходить через 2 і 4 чверті – 2 бісекторною площиною і позначається буквою U.
Запитання для самоперевірки